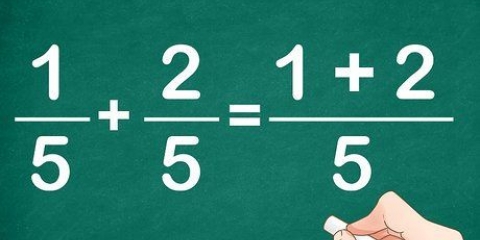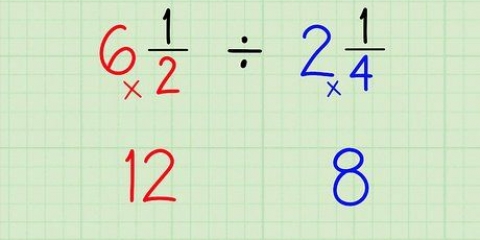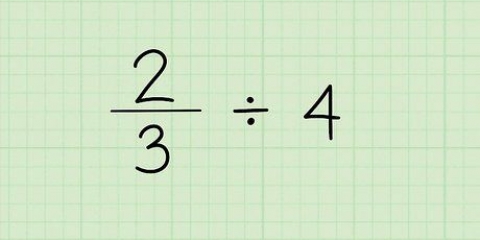Dividindo Frações por Frações: 12 Passos (com Imagens)

Contente

Degraus
- Parte 1 de 2: Entendendo como funciona
- Parte 2 de 2: Dividindo frações por frações - exemplos

Dividir uma fração por uma fração pode parecer confuso no começo, mas na verdade é muito simples. Tudo o que você precisa fazer é inverter a fração de baixo ou a segunda fração e depois multiplicar as duas frações! Este artigo mostrará como fazer isso e mostrará que dividir frações por frações não deve ser um problema.

Degraus

Parte 1 de 2: Entendendo como funciona

Imagem intitulada Dividir frações por frações Etapa 1

1. Pense no que significa dividir por uma fração.O exercício 2 ÷ 1/2 diz o mesmo que: "Quantas vezes ½ vai em 2?”A resposta é 4, porque você pode dividir 2 em 4 metades.

Tente também pensar neste problema em termos de copos de água: Quantos meios copos de água existem em 2 copos de água?? Você pode resolver isso despejando 2 meio copos de água em outro copo, para que no final você tenha 2 copos cheios de água: 2 meio/1 copo * 2 copos = 4 meio copos.
Isso significa que se você dividir um número por um número entre 0 e 1, a resposta sempre será maior que esse número! Isso é verdade se você dividir um número inteiro ou uma fração por outra fração.

Imagem intitulada Dividir frações por frações Etapa 2

2. A divisão é o oposto da multiplicação.Então você também pode pensar em dividir por uma fração como multiplicar pelo inverso dessa fração.O inverso de uma fração é o que diz, simplesmente trocando o numerador e o denominador. Em um momento vamos dividir frações por frações multiplicando pelo inverso do denominador, mas por enquanto vamos ver algumas inversas de frações:

O recíproco de 3/4 é 4/3.

A recíproca de 7/5 é 5/7.

O recíproco de 1/2 é 2/1 e, portanto, 2.

Imagem intitulada Dividir frações por frações Etapa 3

3. Lembre-se dos seguintes passos para dividir uma fração por outra fração.Aqui estão os passos em ordem:

Deixe o contador inalterado.

Faça do sinal de divisão uma multiplicação.

Faça o inverso da segunda fração.

Multiplique os numeradores das duas frações. O resultado será o contador da sua resposta.

Multiplique os denominadores das duas frações. O resultado será o denominador da sua resposta.

Simplifique a fração.

Imagem intitulada Dividir frações por frações Etapa 4

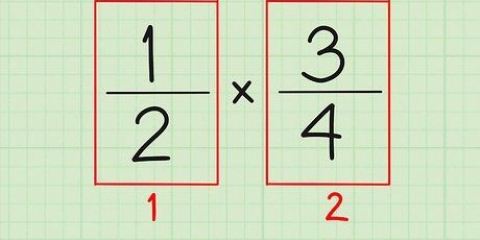
4. Trabalhe com essas etapas no exemplo 1/3 ÷ 2/5.Deixamos o numerador (a primeira fração) inalterado e mudamos o sinal de divisão para um sinal de vezes:

1/3 ÷ 2/5 = está se tornando:

1/3 * __ =

Agora giramos a segunda fração (2/5). Isso então se torna 5/2:

1/3 * 5/2 =

Agora multiplicamos os numeradores das duas frações, 1*5 = 5.

1/3 * 5/2 = 5/

Agora multiplicamos os denominadores das duas frações, 3*2 = 6.

Agora temos: 1/3 * 5/2 = 5/6

Esta fração em particular não pode ser simplificada ainda mais, então agora temos nossa resposta.

Imagem intitulada Dividir frações por frações Etapa 5

5. Tente lembrar o seguinte:"Dividir por uma fração é o mesmo que multiplicar pelo inverso."

Parte 2 de 2: Dividindo frações por frações - exemplos

Imagem intitulada Dividir frações por frações Etapa 6

1. Comece com um problema de exemplo. Suponha que temos a tarefa 2/3 3/7. A questão aqui é com que frequência 3/7 cabe em 2/3. Não entrar em pânico; não é tão difícil quanto parece!

Imagem intitulada Dividir frações por frações Etapa 7

2. Faça do sinal de divisão um sinal de multiplicação. A tarefa agora se torna: 2/3 * __ (vamos preencher o campo vazio em um momento.)

Imagem intitulada Dividir frações por frações Etapa 8

3. Agora determinamos o inverso da segunda fração.Isso significa que viramos 3/7 para que o numerador se torne 3 e o denominador se torne 7.A recíproca de 3/7 é 7/3.Agora vamos escrever o novo problema:

2/3 * 7/3 = __

Imagem intitulada Dividir frações por frações Etapa 9

4. Multiplique as frações.Primeiro, multiplicamos os numeradores das duas frações: 2 * 7 = 14.14 é o numerador da sua resposta.Em seguida, multiplicamos os denominadores das duas frações:3 * 3 = 9.9 é o denominador da sua resposta.Agora você sabe que 2/3 * 7/3 = 14/9.

Imagem intitulada Dividir frações por frações Etapa 10

5. Simplifique a fração.Nesse caso, como o numerador da fração é maior que o denominador, sabemos que a fração é maior que 1 e precisamos convertê-la em um número misto.(Um número misto é um número inteiro com uma fração, como 1 2/3.)

Compartilhe o contador primeiro 14 por meio de 9.9 vai para 14 uma vez, com um resto de 5, então você pode escrever isso como: 1 5/9.

Você pode parar agora, porque você encontrou a resposta! Você pode ver que essa fração não pode ser simplificada ainda mais, porque 9 não é totalmente divisível por 5 e porque o numerador é um número primo.

Imagem intitulada Dividir frações por frações Etapa 11

6. Vamos tentar outro exemplo!Suponha que temos o seguinte problema 4/5 2/6 =.Primeiro, mude o sinal de divisão para um sinal de multiplicação (4/5 * __ =), então encontre o recíproco de 2/6, que é 6/2.Agora a tarefa é a seguinte: 4/5 * 6/2 =__.Agora multiplicamos os numeradores, 4 * 6 = 24, e os denominadores 5*2 = 10.Agora temos o seguinte:4/5 * 6/2 = 24/10.Simplifique a fração. Como o numerador é maior que o denominador, precisaremos convertê-lo em uma fração mista.

Primeiro divida o numerador pelo denominador, (24/10 = 2 restante 4).

Escreva a resposta como 2 4/10. Mas podemos simplificar ainda mais essa fração!

Observe que 4 e 10 são ambos números pares, então o primeiro passo é simplificar dividindo ambos por 2.A fração agora é 2/5.

Como o denominador (5) não se encaixa completamente no numerador (2) e também é primo, você sabe que não pode simplificar ainda mais essa fração. Então a resposta é: 2 2/5.

Imagem intitulada Dividir frações por frações Etapa 12

7. Saiba mais sobre como simplificar frações. Você pode ter aprendido tudo isso uma vez, mas nunca é demais atualizar todo esse conhecimento perdido mais uma vez. Vários artigos podem ser encontrados na internet para melhorar essas habilidades novamente.