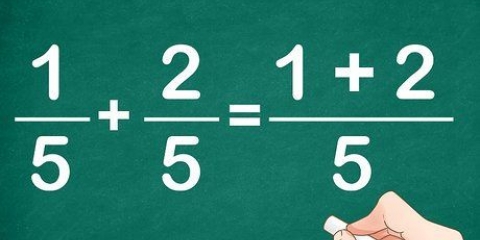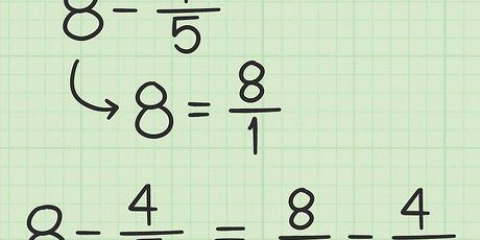(/2) = /2 × /2 ou (/2). Quadrar cada número dá (/4). 
O numerador fica em cima da fração e o denominador fica embaixo. Por exemplo: (/2) = (/2 x 2) = (/4). 
Para converter isso em um número misto, divida 25 por 4. Isso é 6 (6 x 4 = 24), com um resto de 1. Portanto, o número misto é 6/4. 

Por exemplo: (-/4) = (–/4) x (–/4) 
Por exemplo: (-2) x (-8) = (+16) 
Continuando com o exemplo, a fração resultante será um número positivo. (–/4) x (–/4) = (+/16) O costume é omitir o sinal de mais dos números positivos. 
Por exemplo: (/16) tem um fator comum de quatro. Divida a fração por 4: 4/4 = 1, 16/4 = 4 Reescreva a fração simplificada: (/4) 

Por exemplo: 16 × (/16) Eleve os parênteses ao quadrado e elimine o fator comum de 16: 16 * /16 * /16 Como você está lidando aqui com um 16 como um inteiro e duas vezes um 16 no denominador, você pode eliminar um deles. Reescreva a equação simplificada: 12 × /16 simplificar /16 dividindo por 4: /4 Multiplicar: 12 × /4 = 36/4 Parte: 36/4 = 9 
Por exemplo: 16 * (/16) Reescreva com o numerador e denominador ao quadrado: 16 * (/16) Subtraia o expoente no denominador: 16 * /16 Imagine os primeiros 16 como um expoente de 1:16. Usando as regras para subtrair potências/expoentes, você subtrai os expoentes um do outro. 16/16, dá 16 = 16 ou 1/16. Agora você continua com /16 Reescreva e simplifique a fração: /16 =* /4. Simplifique: 12 × /4 = 36/4 Parte: 36/4 = 9
Frações quadradas
Contente
Quadrar frações é uma das operações mais simples que você pode realizar em frações. É muito semelhante ao quadrado de números inteiros, pois você pode simplesmente multiplicar o numerador e o denominador por eles mesmos. Existem alguns casos em que simplificar a fração antes de elevar ao quadrado torna o procedimento mais fácil. Se você ainda não aprendeu essa habilidade, este artigo fornece uma breve visão geral para melhorar sua compreensão.
Degraus
Parte 1 de 3: Frações ao quadrado

1. Entenda como quadrado inteiros. Quando você vê um número elevado à segunda potência, você sabe elevar o número ao quadrado. Isso é o mesmo que multiplicar o número por ele mesmo. Por exemplo:
- 5 = 5 × 5 = 25

2. Você percebe que a quadraturafrações funciona da mesma maneira. Para elevar ao quadrado uma fração, multiplique a fração por ela mesma. Outra maneira de pensar sobre isso é multiplicar o numerador por ele mesmo e o denominador por ele mesmo. Por exemplo:

3. Multiplique o numerador por ele mesmo e o denominador por ele mesmo. A ordem real na qual você multiplica esses números por si mesmos não importa, desde que você eleve os dois números ao quadrado. Para manter as coisas simples, comece com o numerador: basta multiplicá-lo por ele mesmo. Depois multiplique o denominador por ele mesmo.

4.Simplificar a fração para embrulhar isso. Ao lidar com frações, o último passo é sempre simplificar a fração para sua forma mais simples ou converter uma fração imprópria em um número misto. Nosso exemplo, /4 é uma fração imprópria porque o numerador é maior que o denominador.
Parte 2 de 3: Quadrando frações com números negativos

1. Procure um sinal de menos na frente da fração. Se você está lidando com uma fração negativa, há um sinal de menos na frente dela. É aconselhável sempre colocar parênteses em torno de um número negativo para que você saiba que o sinal de menos se refere ao número e não se destina a uma soma de menos.
- Por exemplo: (-/4)

2. Multiplique a fração por ela mesma. Eleve a fração ao quadrado como faria normalmente, multiplicando o numerador por ele mesmo e depois multiplicando o denominador por ele mesmo. Você também pode simplesmente multiplicar a fração por ela mesma.

3. Entenda que a multiplicação de dois números negativos resulta em um número positivo. Quando um sinal de menos está presente, toda a fração se torna negativa. Quando você eleva a fração ao quadrado, você multiplica dois números negativos. Quando dois números negativos são multiplicados, o produto é sempre positivo.

4. Remova o sinal de menos após o quadrado. Se você elevou a fração ao quadrado, multiplicou dois números negativos. Isso significa que a fração quadrada é positiva. Não se esqueça de omitir o sinal de menos na resposta final.

5. Simplifique a fração o máximo possível. O passo final para fazer cálculos fracionários é simplificar. As frações impróprias devem primeiro ser simplificadas para números mistos e depois simplificadas ainda mais.
Parte 3 de 3: Usando simplificações e correções rápidas

1. Verifique se você pode fazer a fraçãosimplificar antes que você esquadre. Geralmente é mais fácil simplificar frações antes de elevar ao quadrado. Lembre-se, simplificar uma fração envolve dividi-la por um fator comum até que 1 seja o único número que resta que pode ser dividido tanto pelo numerador quanto pelo denominador. Simplificar uma fração primeiro significa que você não precisa simplificá-la novamente no final, quando os números são maiores.
- Por exemplo: (/16)
- 12 e 16 podem ser divididos por 4. 12/4 = 3 e 16/4 = 4; assim você pode/16 simplificar para /4.
- Agora você pode fazer a fração /4 ao quadrado.
- (/4) = /16, que você não pode simplificar mais.
- Para provar isso, elevamos ao quadrado a fração original sem simplificar:
- (/16) = (/16x16) = (/256)
- (/256) tem um fator comum de 16. Dividir o numerador e o denominador por 16 simplifica a fração para (/16), a mesma fração que obtivemos simplificando primeiro.

2. Aprenda quando adiar a simplificação de uma fração. Você está lidando com algo mais complexo equações, então pode ser possível eliminar um dos fatores. Nesse caso, portanto, é mais conveniente esperar simplificando a fração. Adicionar um fator extra ao exemplo acima torna isso mais claro.

3. Entenda como fazer isso rapidamente com oexpoente. Outra maneira de resolver o mesmo problema é primeiro simplificar o expoente. O resultado será o mesmo, apenas obtido por uma rota diferente.
Necessidades
- Papel ou um computador
- Lápis/caneta (se estiver usando papel)
Artigos sobre o tópico "Frações quadradas"
Оцените, пожалуйста статью
Popular