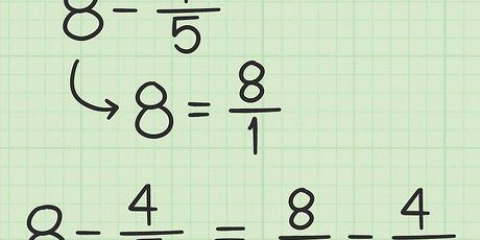Resolvendo Frações Equivalentes: 8 Passos (com Imagens)

Contente

Degraus
- Método 1 de 2: Criando frações equivalentes
- Método 2 de 2: Resolvendo frações equivalentes com variáveis
Pontas
Avisos

Duas frações são "equivalente" se tiverem o mesmo valor. Por exemplo, as frações 1/2 e 2/4 são equivalentes porque 1 sobre 2 tem o mesmo valor que 2 sobre 4 (0,5 na forma decimal). Saber como converter uma fração em outra, ainda que fração equivalente, é um valor matemático essencial que você precisa, da álgebra básica à matemática avançada. Veja o Passo 1 para começar!

Degraus

Método 1 de 2: Criando frações equivalentes

Imagem intitulada Do Equivalent Fractions Step 1

1. Multiplique o numerador e o denominador de uma fração pelo mesmo número para obter uma fração equivalente. Duas frações diferentes, mas equivalentes por definição, numeradores e denominadores que são múltiplos um do outro. Em outras palavras, multiplicar o numerador e o denominador de uma fração pelo mesmo número produzirá uma fração equivalente. Mesmo que os números nesta nova fração sejam diferentes, ela ainda tem o mesmo valor.

Por exemplo, se pegarmos a fração 4/8 e multiplicarmos o numerador e o denominador por 2, obtemos (4×2)/(8×2) = 16/08. Essas duas frações são equivalentes.

(4×2)/(8×2) é essencialmente o mesmo que 4/8 × 2/2. Lembre-se que quando multiplicamos duas frações fazemos assim - numerador vezes numerador e denominador vezes denominador. Observe que 2/2 é igual a 1. Então é fácil ver porque 4/8 é igual a 8/16 - a segunda fração é a primeira fração multiplicada por 2!

2. Divida o numerador e denominador ou uma fração pelo mesmo número para obter uma fração equivalente. Como a multiplicação, a divisão também pode ser usada para criar uma nova fração equivalente à fração dada. Basta dividir o numerador e denominador de uma fração pelo mesmo número para obter uma fração equivalente. Há uma ressalva aqui - a fração resultante deve consistir em números inteiros no numerador e no denominador para ser válida.

Por exemplo, vamos pegar 4/8 novamente. Se, em vez de multiplicar, dividirmos o numerador e o denominador por 2, obtemos (4 2)/(8 ÷ 2) = 2/4. 2 e 4 são ambos números inteiros, então esta fração equivalente é válida.

Imagem intitulada Do Equivalent Fractions Step 2

3. Simplifique sua fração usando o máximo divisor comum (GGD). Qualquer fração tem um número infinito de frações equivalentes - você pode multiplicar o numerador e o denominador por qualquer inteiro, grande ou pequeno obter uma fração equivalente. Mas a forma mais simples de uma dada fração é geralmente aquela com os menores termos. Nesse caso, o numerador e o denominador são tão pequenos quanto possível - eles não podem mais ser divididos por nenhum número inteiro para tornar o termo ainda menor. Para simplificar uma fração, dividimos o numerador e o denominador pelo máximo divisor comum.

O máximo divisor comum (GGD) do numerador e denominador é o maior inteiro pelo qual o numerador e o denominador são divisíveis. Então, em nosso exemplo 4/8, porque 4 é o maior divisor de 4 e 8, dividimos o numerador e o denominador da nossa fração por 4 para obter os termos mais simples. (4 4)/(8 ÷ 4) = 1/2.

Imagem intitulada Do Equivalent Fractions Step 8

4. Se desejar, converta números mistos em frações impróprias para facilitar a conversão. É claro que nem todas as frações que você encontrar serão tão fáceis de simplificar quanto 4/8. Por exemplo, números mistos (ex. 1 3/4, 2 5/8, 5 2/3, etc.) pode tornar essa conversão um pouco mais difícil. Se você quiser fazer uma fração de um número misto, você pode fazer isso de duas maneiras: transforme o número misto em uma fração imprópria e continue, ou mantenha o número misto e dê um número misto como resposta.

Para converter uma fração imprópria, multiplique o inteiro do número misto pelo denominador da fração e adicione o produto ao numerador. Por exemplo, 1 2/3 = ((1 × 3) + 2)/3 = 5/3. Então você pode convertê-lo novamente, se necessário. Por exemplo, 5/3 × 2/2 = 6/10, ainda o mesmo que 1 2/3.

No entanto, a conversão de uma fração imprópria não é necessária. Podemos ignorar o inteiro e apenas converter a fração e depois adicionar o inteiro a ela. Por exemplo, em 3 4/16, estamos olhando apenas para 4/16. 4/16 ÷ 4/4 = 1/4. Então agora adicionamos o inteiro novamente e obtemos um novo número misto, 3 1/4.

5. Nunca adicione ou subtraia para obter frações equivalentes. Ao converter frações para sua forma equivalente, é importante lembrar que as únicas operações que você aplica são multiplicação e divisão. Nunca use adição ou subtração. A multiplicação e a divisão funcionam para obter frações equivalentes porque essas operações são na verdade formas do número 1 (2/2, 3/3, etc.).) e dê respostas que sejam iguais à fração com a qual você começou. Adição e subtração não têm essa capacidade.

Por exemplo, acima descobrimos que 4/8 ÷ 4/4 = 1/2 . Se adicionarmos 4/4 a isso, teríamos uma resposta completamente diferente. 4/8 + 4/4 = 4/8 + 8/8 = 12/8 = 1 1/2 ou 3/2, e nenhum deles é igual a 4/8.

Método 2 de 2: Resolvendo frações equivalentes com variáveis

1. Use a multiplicação cruzada para resolver problemas de equivalência de frações. Um tipo complicado de problema de álgebra que lida com frações equivalentes envolve equações com duas frações, onde uma ou ambas contêm uma variável. Em casos como esse, sabemos que essas frações são equivalentes porque são os únicos termos de cada lado do sinal de igual de uma equação, mas nem sempre é óbvio como resolver a variável. Felizmente, podemos multiplicar por cruz, resolver esse tipo de problema sem problemas.

A multiplicação cruzada é exatamente o que parece - você está multiplicando de maneira cruzada sobre o sinal de igual. Em outras palavras, você multiplica o numerador de uma fração pelo denominador da outra fração e vice-versa. Então você resolve a equação ainda mais.
Por exemplo, temos a equação 2/x = 10/13. Agora multiplique de forma cruzada: multiplique 2 por 13 e 10 por x, e trabalhe a equação ainda mais:

2×13 = 26
10 × × = 10 ×
10x = 26. Agora vamos trabalhar a equação ainda mais. x = 26/10 = 2.6

2. Use a multiplicação cruzada da mesma forma que as equações multivariadas ou expressões variáveis. Uma das melhores características da multiplicação cruzada é que ela funciona praticamente da mesma forma, quer você esteja lidando com duas frações simples ou complexas. Por exemplo, se ambas as frações contiverem variáveis, nada mudará - você só terá que se livrar dessas variáveis. Da mesma forma, se os numeradores ou denominadores de sua variável fracionária contiverem expressões, apenas "continuar a multiplicar" usando a propriedade distributiva e resolvendo como você costuma fazer.

Por exemplo, suponha que temos a equação ((x + 3)/2) = ((x + 1)/4). Nesse caso, resolvemos isso por multiplicação cruzada:

(x + 3) × 4 = 4x + 12

(x + 1) × 2 = 2x + 2

2x + 2 = 4x + 12

2 = 2x + 12

-10 = 2x

-5 = x

3. Usar técnicas para resolver polinômios. A multiplicação cruzada não funciona sempre um resultado que você pode resolver com álgebra simples. Se você estiver lidando com termos variáveis, obterá rapidamente uma equação quadrática ou outro polinômio como resultado. Nesses casos, você usa, por exemplo, o quadrado e/ou a fórmula do quadrado.

Por exemplo, tomamos a equação ((x +1)/3) = (4/(2x - 2)). Primeira multiplicação cruzada:

(x + 1) × (2x - 2) = 2x + 2x -2x - 2 = 2x - 2

4×3 = 12

2x - 2 = 12. Neste ponto, queremos converter isso em uma equação quadrática (ax + bx + c = 0) subtraindo 12 de ambos os lados, dando 2x - 14 = 0. Agora usamos a fórmula (x = (-b +/- √(b - 4ac))/2a) para encontrar o valor de x:

x = (-b +/- √(b - 4ac))/2a. Em nossa equação, 2x - 14 = 0, a = 2, b = 0 ec = -14.

x = (-0 +/- √(0 - 4(2)(-14))))/2(2)

x = (+/- √( 0 - -112))/2(2)

x = (+/- √(112))/2(2)

x = (+/- 10.58/4)

x = +/- 2.64 Neste ponto, verificamos nossa resposta substituindo 2,64 e -2,64 na equação quadrática original.

Pontas

Converter frações para uma forma equivalente é na verdade como multiplicar por uma fração como 2/2 ou 5/5. Como isso é, em última análise, igual a 1, o valor da fração permanece o mesmo.