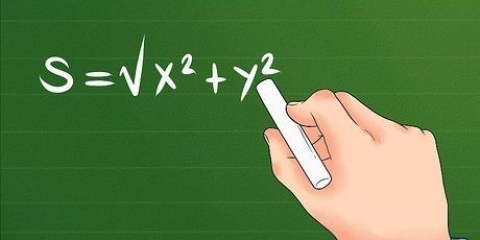Calculando a Covariância

Contente

Degraus
Avisos

A covariância é um cálculo estatístico para tornar a relação entre dois conjuntos de dados mais transparente. Suponha, por exemplo, que antropólogos estudem a altura e o peso de uma população dentro de uma cultura particular. Para cada pessoa no estudo, altura e peso podem ser representados com um par de dados (x, y). Esses valores podem ser usados em uma fórmula padrão para calcular a relação de covariância. Este artigo explica primeiro os cálculos para determinar a covariância de um conjunto de dados. A seguir, duas outras formas automatizadas de determinar o resultado serão discutidas.

Degraus

Método 1 de 4: Calculando a covariância manualmente usando a fórmula padrão

Imagem intitulada Calcular Covariância Etapa 1

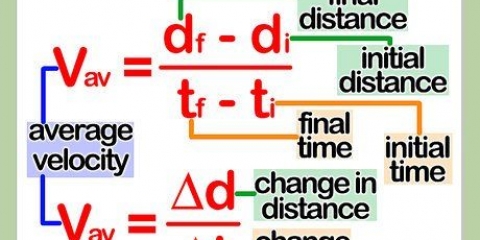
1. Aprenda a fórmula de covariância padrão e suas partes. A fórmula padrão para calcular a covariância é

Σ (X eu - X_{média}) (y_{eu} - y_{média}) / (n - 1)

$Sigma (x_{i}-x_{{text{avg}}})(y_{i}-y_{{text{avg}}})/(n-1)$ . Para usar esta fórmula, você precisa saber o significado das variáveis e símbolos:

$Σ$ $Sigma$ - Este símbolo é a letra grega `sigma`. Em funções matemáticas, isso significa adicionar uma série do que segue. Nesta fórmula, o sinal Σ significa que você calcula os valores no numerador da fração, depois soma todos e depois divide o total pelo denominador.
$X eu$ $XI}$ - Você pode ler esta variável como `x sub i`. O subscrito i representa um contador. Isso significa que você fará um cálculo para cada valor de x em seu conjunto de dados.
$X uma v g$ $x_{{média}}$ - O `avg` indica que x(avg) é o valor médio de todos os x pontos de dados. A média às vezes é escrita como um x com uma pequena linha horizontal acima dela. Nesse estilo, você lê a variável como `x-bar`, mas ainda significa a média do conjunto de dados.
$y eu$ $s_{i}$ - Você pode ler esta variável como `y sub i`. O subscrito i é o numerador. Isso significa que você fará um cálculo para cada valor de y em seu conjunto de dados.
$y uma v g$ $y_{{média}}$ - O `avg` indica que y(avg) é o valor médio de todos os x pontos de dados. A média às vezes é escrita como um y com uma pequena linha horizontal acima dela. Nesse estilo você lê a variável como `y-bar`, mas ainda significa a média do conjunto de dados.
$n$ $n$ - Esta variável é o número de elementos em seu conjunto de dados. Lembre-se que em um problema de covariância, um único `elemento` é composto por um valor x e um valor y. O valor `n` é o número de pares de pontos de dados, não números individuais.

Imagem intitulada Calcular Covariância Passo 2

2. Construa sua tabela de dados. Antes de começar, é útil coletar seus dados. Criar uma tabela com cinco colunas. Você deve declarar cada coluna da seguinte forma:

X

$X$ - Preencha esta coluna com os valores dos pontos dos dados x.

y

$y$ - Preencha esta coluna com os valores dos dados y. Certifique-se de que os valores de y estejam alinhados com os valores de x correspondentes. Em um problema de covariância, a ordem dos pontos de dados e o acoplamento de x e y são importantes.

(X eu - X_{média})

$(x_{i}-x_{{text{média}}})$ - Deixe esta coluna em branco no início. Você vai preenchê-lo com dados depois de calcular a média dos dados x.

(y eu - y_{média})

$(y_{i}-y_{{text{avg}}})$ - Deixe esta coluna vazia no início. Você vai preenchê-lo com dados depois de calcular a média dos dados y.

produtos

${text{Produto}}$ - Deixe a última coluna vazia também. Este será preenchido durante o processamento da atribuição.

Imagem intitulada Calcular Covariância Etapa 3

3. Calcule a média dos x pontos de dados. Esta coleção de dados de amostra contém 9 números. Para encontrar a média, some-os e divida a soma por 9. Isso dá o resultado 1 + 3 + 2 + 5 + 8 + 7 + 12 + 2 + 4 = 44. Quando você divide isso por 9, obtém a média de 4,89. Este é o valor que você usará como x(avg) para os próximos cálculos.

Imagem intitulada Calcular Covariância Passo 4

4. Calcule a média dos pontos de dados y. Esta coluna y também deve consistir em 9 pontos de dados que coincidem com os pontos de dados x. Determine a média deste. Para este conjunto de dados de amostra, torna-se 8 + 6 + 9 + 4 + 3 + 3 + 2 + 7 + 7 = 49. Divida esse total por 9 para obter uma média de 5,44. Você vai usar 5,44 como o valor de y(avg) para os próximos cálculos.

Imagem intitulada Calcular Covariância Passo 5

5. Calcule os valores (Xeu-Xmédia){displaystyle (x_{i}-x_{text{avg}})} $(x_{i}-x_{{text{média}}})$ . Para cada elemento na coluna x, calcule a diferença entre esse número e o valor médio. Para este problema de exemplo, isso significa subtrair 4,89 de cada valor x. Se o ponto de dados original for menor que a média, seu resultado será negativo. Se o ponto de dados original for maior que a média, o resultado será positivo. Certifique-se de acompanhar quais valores são negativos.

Por exemplo, o primeiro ponto de dados na coluna x é 1. O valor a ser inserido na primeira linha da coluna

(X eu - X_{média})

$(x_{i}-x_{{text{média}}})$ é: 1 – 4,89 = -3,89.

Repita este processo para cada ponto de dados. Então a segunda linha se torna: 3 - 4,89 = -1.89. A terceira linha se torna: 2 - 4,89 = -2,89. Continue este processo para todos os pontos de dados. Os nove números nesta coluna se tornam: -3,89, -1,89, -2,89, 0,11, 3,11, 2,11, 7,11, -2,89, -0,89.

Imagem intitulada Calcular Covariância Passo 6

6. Calcule os valores (yeu-ymédia){displaystyle (y_{i}-y_{text{avg}})} $(y_{i}-y_{{text{avg}}})$ . Nesta coluna, você fará subtrações semelhantes, usando os pontos de dados y e a média y. Se o ponto de dados original for menor que a média, o resultado será negativo. Se o ponto de dados original for maior que a média, seu resultado será positivo. Certifique-se de acompanhar quais valores são negativos.

Então, para a primeira linha, seu cálculo será: 8 -5,44, = 2,56.

A segunda linha se torna: 6 – 5,44 = 0,56.

Continue subtraindo os valores até o final da lista de dados. Quando terminar, você deverá ter os seguintes nove valores nesta coluna: 2,56, 0,56, 3,56, -1,44, -2,44, -2,44, -3,44 , 1,56, 1,56.

Imagem intitulada Calcular Covariância Passo 7

7. Calcular os produtos para cada linha de dados. Você preenche as linhas da última coluna multiplicando os números que você calculou nas duas colunas anteriores de

(X eu - X_{média})

$(x_{i}-x_{{text{média}}})$ e

(y eu - y_{média})

$(y_{i}-y_{{text{avg}}})$ . Trabalhe do seu jeito linha por linha, multiplicando os dois números pelos pontos de dados correspondentes. Fique atento a quaisquer valores negativos ao longo do caminho.

Na primeira linha desses dados de amostra, o

(X eu - X_{média})

$(x_{i}-x_{{text{média}}})$ você calculou -3,89, e o

(y eu - y_{média})

$(y_{i}-y_{{text{avg}}})$ valor 2,56. O produto desses dois números é: -3,89 x 2,56 = -9,96.

Para a segunda linha, multiplique os dois números: -1,88 x 0,56 = -1,06.

Continue multiplicando linha por linha até o final do conjunto de dados. Quando terminar, os nove valores nesta coluna devem ser: -9,96, -1,06, -10,29, -0,16, -7,59, -5,15, -24,46 , -4,51, -1,39.

Imagem intitulada Calcular Covariância Passo 8

8. Encontre a soma dos valores na última coluna. É aqui que entra o símbolo Σ. Depois de fazer todos os cálculos até agora, some os resultados. Para este conjunto de dados de exemplo, agora você deve ter nove valores na última coluna. Adicione esses nove números juntos. Preste muita atenção se um número é positivo ou negativo.

A soma deste conjunto de dados de amostra deve somar -64,57. Escreva esse total no espaço na parte inferior da coluna. Este é o valor do numerador da fórmula de covariância padrão.

Imagem intitulada Calcular Covariância Passo 9

9. Calcule o denominador da fórmula de covariância. O numerador da fórmula de covariância padrão é o valor que você acabou de calcular. O denominador é representado por (n-1) e é um a menos que o número de pares de dados em seu conjunto de dados.

Neste problema de exemplo, existem nove pares de dados, então n é 9. Portanto, o valor de (n-1) é igual a 8.

Imagem intitulada Calcular Covariância Passo 10

10. Divida o numerador pelo denominador. O último passo no cálculo da covariância é dividir o numerador,

Σ (X eu - X_{média}) (y_{eu} - y_{média})

$Sigma (x_{i}-x_{{text{avg}}})(y_{i}-y_{{text{avg}}})$ pelo denominador,

(n - 1)

$(n-1)$ . O quociente é a covariância dos seus dados.

Para este conjunto de dados de amostra, este cálculo é: -64,57/8 = -8,07.

Método 2 de 4: Calcular a covariância usando uma planilha do Excel

Imagem intitulada Calcular Covariância Passo 11

1. Observe quais são os cálculos repetitivos. Covariância é um cálculo que você precisa fazer manualmente algumas vezes para entender o significado do resultado. No entanto, se você usar covariância rotineiramente para interpretar dados, precisará de uma maneira mais rápida e automatizada de obter os resultados. Você já deve ter notado que, com nosso conjunto de dados relativamente pequeno de apenas nove pares de dados, os cálculos consistiam em duas médias, dezoito subtrações separadas, nove multiplicações, uma adição e, finalmente, outra divisão. São 31 cálculos relativamente pequenos para encontrar a solução. Ao longo do caminho, você corre o risco de perder os sinais negativos ou copiar os resultados incorretamente, fazendo com que a resposta fique incorreta.

Imagem intitulada Calcular Covariância Passo 12

2. Criar uma planilha para calcular a covariância. Se você estiver familiarizado com o Excel (ou qualquer outro programa de cálculo), poderá criar facilmente uma tabela para determinar a covariância. Rotule os títulos das cinco colunas como nos cálculos manuais: x, y, (x(i)-x(avg)), (y(i)-y(avg)) e Product.

Para simplificar a nomenclatura, nomeie a terceira coluna como "diferença x" e a quarta coluna "diferença y", contanto que você se lembre do significado dos dados.

Se a tabela começar no canto superior esquerdo da planilha, a célula A1 será rotulada como x, enquanto os outros rótulos continuarão na célula E1.

Imagem intitulada Calcular Covariância Passo 13

3. Preencha os pontos de dados. Digite os valores dos dados nas duas colunas x e y. Lembre-se de que a ordem dos pontos de dados é importante, portanto, você deve combinar cada y com o valor correspondente de x.

Os valores x começam na célula A2 e continuam até o número de pontos de dados que você precisa.

Os valores de y começam na célula B2 e continuam até o número de pontos de dados que você precisa.

Imagem intitulada Calcular Covariância Passo 14

4. Determine as médias dos valores de x e y. O Excel calcula as médias para você muito rapidamente. Na primeira célula em branco em cada coluna de dados, digite a fórmula =MÉDIA(A2:A___). Preencha o espaço em branco com o número da célula que corresponde ao seu último ponto de dados.

Por exemplo, se você tiver 100 pontos de dados, as células A2 a A101 serão preenchidas, então na célula você digitaria: = AVERAGE(A2:A101).

Para os dados y, digite a fórmula = AVERAGE(B2:B101).

Lembre-se de que uma fórmula no Excel começa com um sinal `=`.

Imagem intitulada Calcular Covariância Passo 15

5. Digite a fórmula para a coluna (x(i)-x(avg)). Na célula C2, insira a fórmula para calcular a primeira subtração. Esta fórmula se torna: =A2-___. Preencha o espaço vazio com o endereço da célula que contém a média dos dados x.

Por exemplo, a média dos 100 pontos de dados é calculada na célula A103, então sua fórmula se torna: =A2-A103.

Imagem intitulada Calcular Covariância Passo 16

6. Repita a fórmula para os pontos de dados (y(i)-y(avg)). Seguindo o mesmo exemplo estará na célula D2. A fórmula se torna: =B2-B103.

Imagem intitulada Calcular Covariância Passo 17

7. Digite a fórmula para a coluna `Produto`. Na quinta coluna você tem que digitar na célula E2 a fórmula para calcular o produto das duas células anteriores. Isso então se torna: =C2*D2.

Imagem intitulada Calcular Covariância Passo 18

8. Copie as fórmulas para preencher a tabela. Até agora você programou apenas os primeiros pontos de dados na linha 2. Usando o mouse, destaque as células C2, D2 e E2. Coloque o cursor na pequena caixa no canto inferior direito até que um sinal de mais apareça. Clique e segure o botão do mouse e arraste o mouse para baixo para expandir a seleção e preencher toda a tabela de dados. Esta etapa copiará automaticamente as três fórmulas das células C2, D2 e E2 para toda a tabela. A tabela deve ser preenchida automaticamente com todos os cálculos.

Imagem intitulada Calcular Covariância Passo 19

9. Programe a soma da última coluna. Você precisa da soma dos itens na coluna `Produto`. Na célula em branco imediatamente abaixo do último ponto de dados nessa coluna, digite a fórmula: =SOMA(E2:E___). Preencha o espaço em branco com o endereço da célula do último ponto de dados.

No exemplo com 100 pontos de dados, esta fórmula vai para a célula E103. Tipo: =SOMA(E2:E102).

Imagem intitulada Calcular Covariância Passo 20

10. Determine a covariância. Você também pode deixar o Excel fazer o cálculo final para você. O último cálculo na célula E103 em nosso exemplo representa o numerador da fórmula de covariância. Imediatamente abaixo dessa célula, digite a fórmula: =E103/___. Preencha o espaço em branco com o número de pontos de dados que você tem. No nosso exemplo é 100. O resultado é a covariância de seus dados.

Método 3 de 4: Usando calculadoras de covariância online

Imagem intitulada Calcular Covariância Passo 21

1. Pesquise online por calculadoras de covariância. Várias escolas, empresas ou outras fontes possuem sites que calculam os valores de covariância com muita facilidade para você. Use o termo de pesquisa `calculadora de covariância` em um mecanismo de pesquisa.

Imagem intitulada Calcular Covariância Passo 22

2. Insira seus dados. Por favor, leia as instruções no site com atenção para certificar-se de inserir as informações corretamente. É importante que seus pares de dados sejam mantidos em ordem, caso contrário o resultado gerado será uma covariância incorreta. Os sites têm diferentes estilos de entrada de dados.

No site http://ncalculators.com/statistics/covariance-calculator.htm, por exemplo existe uma caixa horizontal para inserir os valores x e uma segunda caixa horizontal para inserir os valores y. Você deve inserir seus dados separados por vírgulas. Portanto, o conjunto de dados x calculado anteriormente neste artigo deve ser inserido como 1,3,2,5,8,7,12,2,4. Os dados y como 8,6,9,4,3,3,2,7,7.

Em outro site, https://www.a calculadora.co/matemática/Covariance-Calculator-705.html, ser-lhe-á pedido que introduza os dados x na primeira caixa. Os dados são inseridos verticalmente, com um item por linha. Portanto, a entrada neste site se parece com:

Imagem intitulada Calcular Covariância Passo 23

3. Calcule seus resultados. O atrativo desses cálculos on-line é que, após inserir os dados, você geralmente só precisa clicar no botão `Calcular`, após o qual os resultados aparecem automaticamente. A maioria dos sites fornecerá os cálculos intermediários de x(avg), y(avg) e n.

Método 4 de 4: Interpretando os resultados da covariância

Imagem intitulada Calcular Covariância Passo 24

1. Procure um relacionamento positivo ou negativo. A covariância é um único número estatístico que indica a relação entre um conjunto de dados e outro. No exemplo mencionado na introdução, a altura e o peso são medidos. Você esperaria que, à medida que as pessoas crescem, seu peso também aumente, levando a uma visão de covariância positiva. Outro exemplo: suponha que os dados sejam coletados indicando o número de horas que uma pessoa pratica golfe e a pontuação que ela alcançou. Nesse caso, você espera uma covariância negativa, o que significa que, à medida que o número de horas de treinamento aumenta, a pontuação do golfe diminui. (No golfe, uma pontuação mais baixa é melhor).

Considere o conjunto de dados de amostra calculado acima. A covariância resultante é -8,07. O sinal de menos significa que à medida que os valores de x aumentam, os valores de y tendem a diminuir. Você pode ver que isso é verdade observando alguns dos valores. Por exemplo, os valores x de 1 e 2 correspondem aos valores y de 7, 8 e 9. Os valores x de 8 e 12 estão ligados aos valores y de 3 e 2. respectivamente.

Imagem intitulada Calcular Covariância Passo 25

2. Interpretar o tamanho da covariância. Se o número da pontuação de covariância for grande, seja um número positivo grande ou um número negativo grande, você poderá interpretar isso como dois elementos de dados fortemente conectados, de maneira positiva ou negativa.

A covariância -8,07 do conjunto de dados de amostra é bastante grande. Observe que os dados variam de 1 a 12. Então 8 é um número bem grande. Isso indica uma relação bastante forte entre os conjuntos de dados x e y.

Imagem intitulada Calcular Covariância Passo 26

3. Entenda a falta de um relacionamento. Se o seu resultado for uma covariância igual ou muito próxima de 0, então você pode concluir que os pontos de dados não têm relação. Ou seja, um aumento em um valor pode, mas não necessariamente, levar a um aumento no outro. Os dois termos estão ligados quase arbitrariamente.

Suponha que você relacione os tamanhos dos sapatos com as notas dos exames. Como existem tantos fatores que afetam as notas dos exames de um aluno, uma pontuação de covariância próxima de 0 é esperada. Isso indica que quase não há relação entre os dois valores.

Imagem intitulada Calcular Covariância Passo 27

4. Visualize o relacionamento graficamente. Para entender a covariância visualmente, você pode plotar seus pontos de dados em um gráfico x,y. Ao fazer isso, você deve ver facilmente que os pontos, embora não estejam exatamente em uma linha reta, tendem a se aproximar de um cluster em uma linha diagonal do canto superior esquerdo ao canto inferior direito. Esta é a descrição de uma covariância negativa. Você também vê que o valor da covariância é -8,07. Este é um número bastante grande em comparação com os pontos de dados. O número alto sugere que a covariância é bastante forte, o que pode ser inferido a partir da forma linear dos pontos de dados.

Para revisar isso novamente, leia os artigos do wikiHow sobre como desenhar pontos em um sistema de coordenadas.

Avisos

A covariância tem aplicação limitada em estatística. Muitas vezes, é um passo para calcular coeficientes de correlação ou outros conceitos. Tenha cuidado com interpretações excessivamente ousadas com base em uma pontuação de covariância.

Artigos sobre o tópico "Calcular covariância"

Calcular variância

Calcular frequência acumulada

Calcular valores atípicos

Calcular distância

Оцените, пожалуйста статью