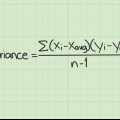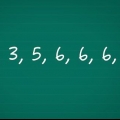Calculando a Variação: 8 Passos (com Imagens)

Contente

Degraus
Pontas

Calcular a variância permite medir a dispersão de um conjunto de valores - o grau em que vários valores diferem uns dos outros. A variância é um dos componentes da distribuição de probabilidade e indica até que ponto os valores se desviam da média. A variância é frequentemente usada em conjunto com o desvio padrão (a raiz quadrada da variância). Se você quiser saber como calcular a variância de um conjunto de valores, siga os passos abaixo.

Degraus

1. Escreva a fórmula para calcular a variância. A estimativa para calcular uma estimativa aleatória da variância populacional de uma amostra fixa de n observações é a seguinte definição:(s) = Σ [(x_eu - x̅)]/n - 1. A fórmula para calcular a variância em uma população inteira é a mesma que a anterior, exceto que o denominador não é igual a n – 1, mas a n. Contanto que você esteja lidando com um conjunto finito de observações, é melhor usar a primeira fórmula. Aqui está uma explicação das variáveis da fórmula:

s = Variação
Σ = Soma, a soma de todos os termos na equação após o sinal de soma.
X_eu = Os valores da amostra.
x̅ = A média dos valores na série.
n = O tamanho da amostra. O número de valores na série.

2. Calcular a soma dos valores da série. Primeiro crie uma tabela com uma coluna para os valores, o valor menos a média (x_eu - x̅) e então o quadrado desses termos [(x_eu - X))]. Depois de terminar a tabela e preencher a primeira coluna, some todos os valores da série. Suponha que você esteja lidando com a seguinte sequência de números: 17, 15, 23, 7, 9, 13. Somado isto é: 17 + 15 + 23 + 7 + 9 + 13 = 84.

3. Calcule a média. Divida a soma dos números da série pelo número de elementos da série para calcular a média. Então, neste caso, a soma 84 dividida pelo número de números, 6. 84/6 = 14. escrever "14" na parte inferior da coluna como uma média.

4. Subtraia a média de cada valor da série. Subtraia 14 de cada valor na série e preencha a terceira coluna (a média da amostra). Você pode verificar seu trabalho verificando se a soma de todos os resultados é zero. Veja como calcular o desvio da média para cada valor na série:

17 - 14 = 3

15 - 14 = 1

23 - 14 = 9

7 - 14 = -7

9 - 14 = -5

13 - 14 = -1

5. Quadrar cada resultado. Depois de calcular o desvio da média, eleve ao quadrado e escreva a resposta na quarta coluna. Então todas as respostas são positivas. Veja como funcionou:

3 = 9

1 = 1

9 = 81

(-7)= 49

(-5) = 25

(-1)= 1

6. Calcular a soma dos quadrados. Adicione os resultados juntos. 9 + 1 + 81 + 49 + 25 + 1 = 166

7. Substitua os valores na equação. Preencha os valores na equação. Lembre-se disso "n" representa o número de elementos na sequência.

s = 166/(6-1)

8. Resolver. Agora divida 166 por 5. O resultado é 33,2. Se você também quiser saber o desvio padrão, encontre a raiz quadrada de 33,2. √33,2 = 5,76. Agora você pode começar a interpretar esses dados em relação ao quadro geral. Normalmente, a variância de duas séries é comparada. O valor mais baixo significa que nessa série a variância é menos grande.