Vamos continuar trabalhando com o exemplo acima. Aqui está nosso conjunto de dados mostrando as temperaturas em graus Fahrenheit de vários objetos em uma sala: {71, 70, 73, 70, 70, 69, 70, 72, 71, 300, 71, 69}. Se ordenarmos os valores do conjunto do menor para o maior, este se torna nosso novo conjunto: {69, 69, 70, 70, 70, 70, 71, 71, 71, 72, 73, 300}. 
Não se confunda com conjuntos de dados com um número par de pontos - a média dos dois pontos do meio geralmente é um número que não está no conjunto de dados em si - tudo bem. No entanto, se os dois pontos médios forem iguais, a média também será obviamente esse número - isso também é OK. No nosso exemplo temos 12 pontos. Os dois termos do meio são os pontos 6 e 7 – 70 e 71 . respectivamente. Portanto, a mediana do nosso conjunto de dados é a média desses dois pontos: ((70 + 71) / 2)=70,5. 
Em nosso exemplo, seis pontos estão acima da mediana e seis abaixo dela. Então, para encontrar o primeiro quartil, precisamos tirar a média dos dois pontos do meio nos seis pontos inferiores. Os pontos 3 e 4 dos seis inferiores são ambos 70, então sua média é ((70 + 70) / 2)=70. Então nosso valor para Q1 é 70. 
Continuando com o exemplo acima, vemos que os dois pontos médios dos seis pontos acima da mediana são 71 e 72. A média desses dois pontos é ((71 + 72) / 2)=71,5. Portanto, nosso valor para o terceiro trimestre é 71,5. 
Em nosso exemplo, os valores para Q1 e Q3 são 70 e 71,5 . respectivamente. Para encontrar o intervalo interquartil, calculamos Q3 - Q1: 71,5 - 70=1,5. Isso funciona mesmo se Q1, Q3 ou ambos os números forem negativos. Por exemplo, se nosso valor para Q1 fosse -70, o intervalo interquartil seria 71,5 - (-70)=141,5, o que está correto. 
Em nosso exemplo, o intervalo interquartil é (71,5 - 70), ou 1,5. Multiplique isso por 1,5 e você terá 2,25. Adicionamos esse número a Q3 e o subtraímos de Q1, para encontrar os limites internos da seguinte forma: 71,5 + 2,25 = 73,75 70 - 2,25=67,75 Assim, as fronteiras internas são 67,75 e 73,75. Em nosso conjunto de dados, apenas a temperatura do forno – 300 graus Fahrenheit – está fora dessa faixa. Então isso pode ser um leve outlier. No entanto, ainda temos que determinar se essa temperatura é uma exceção extrema, então não vamos tirar conclusões precipitadas ainda.

Em nosso exemplo, multiplicamos o intervalo interquartil por 3 e chegamos a (1,5 * 3) ou 4,5. Agora podemos encontrar os limites externos da mesma maneira que os limites internos: 71,5 + 4,5=76 70 - 4,5=65,5 Então os limites externos são 65,5 e 76. Os pontos de dados que estão fora das fronteiras externas são considerados extremos extremos. Em nosso exemplo, a temperatura do forno, 300 graus Fahrenheit, está bem fora dos limites externos. Então a temperatura do forno é seguro um extremo extremo.

Outro critério a ser considerado é se os outliers afetam a média de um conjunto de dados de forma distorcida ou enganosa. Isso é especialmente importante se você pretende tirar conclusões da média do seu conjunto de dados. Vamos revisar nosso exemplo. Desde que altamente Embora seja improvável que o forno tenha atingido uma temperatura de 300°F devido a alguma força imprevista da natureza, em nosso exemplo podemos concluir com quase 100% de certeza que o forno foi deixado ligado acidentalmente, resultando em uma leitura de temperatura anormalmente alta. Além disso, se não removermos o valor discrepante, nosso conjunto de dados terá uma média de (69 + 69 + 70 + 70 + 70 + 70 + 71 + 71 + 71 + 72 + 73 + 300)/12=89,67 °F, enquanto a média sem o valor atípico sai em (69 + 69 + 70 + 70 + 70 + 70 + 71 + 71 + 71 + 72 + 73)/11=70,55 °F. Como o valor atípico foi causado por erro humano e como é incorreto dizer que a temperatura média da sala estava próxima de 32°C, devemos optar por escolher nosso valor atípico remover. 
Por exemplo, imagine que estamos projetando um novo medicamento para aumentar o tamanho dos peixes em uma piscicultura. Vamos usar nosso conjunto de dados antigo ({71, 70, 73, 70, 70, 69, 70, 72, 71, 300, 71, 69}), exceto que cada ponto agora representa a massa de um peixe (em gramas) após tratamento com outra droga experimental desde o nascimento. Em outras palavras, a primeira droga deu a um peixe uma massa de 71 gramas, a segunda deu a outro peixe uma massa de 70 gramas e assim por diante. Nesta situação 300 . é ainda um grande outlier, mas não devemos removê-lo agora. Porque, se assumirmos que o outlier não é resultado de um erro, representa um grande sucesso em nosso experimento. A droga que produziu um peixe de 300 gramas funcionou melhor do que qualquer outra droga, então é isso a maioria ponto de dados importante em nosso conjunto, em vez do ao menos ponto de dados importante.
Calcular valores atípicos
Contente
UMA ponto fora da curva ou ponto fora da curva em estatística, um ponto de dados que difere significativamente dos outros pontos de dados em uma amostra. Muitas vezes, os outliers apontam para anomalias ou erros nas medições dos estatísticos, após o que eles podem remover o outlier do conjunto de dados. Se eles realmente optarem por remover os valores discrepantes do conjunto de dados, isso poderá trazer mudanças significativas nas conclusões extraídas do estudo. É por isso que é importante calcular e determinar valores discrepantes se você deseja interpretar corretamente os dados estatísticos.
Degraus

1. Saiba como identificar potenciais outliers. Antes de podermos decidir se removemos valores anômalos de um determinado conjunto de dados, é claro que devemos reconhecer os possíveis valores discrepantes no conjunto de dados. Em geral, os outliers são os pontos de dados que se desviam significativamente da tendência que os outros valores no conjunto formam – em outras palavras, eles atirar para fora dos outros valores. Geralmente é fácil reconhecer isso em tabelas e (especialmente) em gráficos. Se o conjunto de dados for representado graficamente visualmente, os valores discrepantes estarão `distantes` dos outros valores. Por exemplo, se a maioria dos pontos em um conjunto de dados formar uma linha reta, os valores discrepantes não estarão de acordo com essa linha.
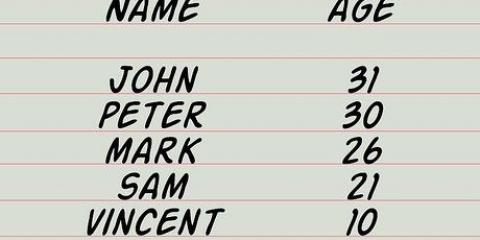
- Vejamos um conjunto de dados mostrando as temperaturas de 12 objetos diferentes em uma sala. Se a temperatura de 11 dos objetos flutuar em torno de 21°C em alguns graus no máximo, enquanto um objeto, um forno, tem uma temperatura de 150°C, você pode ver rapidamente que o forno é provavelmente um valor atípico.

2. Classifique todos os pontos de dados de baixo para alto. O primeiro passo no cálculo de outliers é encontrar o valor mediano (ou o valor médio) do conjunto de dados. Essa tarefa fica muito mais fácil se os valores do conjunto estiverem em ordem do menor para o maior. Então, antes de continuar, classifique os valores em seu conjunto de dados assim.

3. Calcule a mediana do conjunto de dados. A mediana de um conjunto de dados é o ponto de dados em que metade dos dados está acima dele e metade dos dados está abaixo - é basicamente o "centro" do conjunto de dados. Se o conjunto de dados contém um número ímpar de pontos, a mediana é fácil de encontrar – a mediana é o ponto com tantos pontos acima quanto abaixo dele. Se houver um número par de pontos, já que não há um ponto médio, você deve tirar a média dos dois pontos médios para encontrar a mediana. Ao calcular os outliers, a mediana geralmente é denotada pela variável Q2 – porque está entre Q1 e Q3, o primeiro e o terceiro quartis. Vamos determinar essas variáveis mais tarde.

4. Calcule o primeiro quartil. Este ponto, que chamamos de variável Q1, é o ponto de dados abaixo do qual 25 por cento (ou um quarto) das observações estão. Em outras palavras, este é o ponto médio de todos os pontos em seu conjunto de dados abaixo a mediana. Se houver um número par de valores abaixo da mediana, você deve novamente calcular a média dos dois valores do meio para encontrar Q1, como você já deve ter feito para determinar a mediana.

5. Calcule o terceiro quartil. Este ponto, que denotamos pela variável Q3, é o ponto de dados acima do qual 25% dos dados estão. Encontrar Q3 é praticamente o mesmo que encontrar Q1, exceto que neste caso estamos olhando para os pontos acima a mediana.

6. Encontre o intervalo interquartil. Agora que determinamos Q1 e Q3, precisamos calcular a distância entre essas duas variáveis. A distância entre Q1 e Q3 pode ser encontrada subtraindo Q1 de Q3. O valor obtido para o intervalo interquartil é crucial para determinar os limites para pontos não desviantes em seu conjunto de dados.

7. Encontre os `limites internos` do conjunto de dados. Você pode identificar valores discrepantes determinando se eles estão dentro de vários limites numéricos; os chamados `valores-limite internos` e `valores-limite externos`. Um ponto que está fora dos limites internos do conjunto de dados é classificado como discrepante leve, e um ponto que está fora dos limites externos é classificado como extremo extremo. Para encontrar os limites internos do seu conjunto de dados, primeiro multiplique o intervalo interquartil por 1,5. Adicione o resultado a Q3 e subtraia-o de Q1. Os dois resultados são os limites internos do seu conjunto de dados.


8. Encontre os `limites externos` do conjunto de dados. Você faz isso da mesma maneira que com os limites internos, com a única diferença de que você multiplica o intervalo interquartil por 3 em vez de 1,5. Você então adiciona o resultado a Q3 e subtrai de Q1 para encontrar os limites externos.


9. Use uma avaliação qualitativa para determinar se você deve “descartar” os valores discrepantes. Com o método acima, você pode determinar se certos pontos são discrepantes leves, discrepantes extremos ou nenhum outlier. Mas não se engane – reconhecer um ponto como um ponto atípico apenas o torna um candidato a ser removido do conjunto de dados, e não imediatamente um ponto removido devo transformar-se em. O montaram por que um outlier é diferente do resto dos pontos no conjunto é crucial para determinar se o outlier deve ser removido. Em geral, os outliers causados por algum erro - um erro nas medições, nas gravações ou no desenho experimental, por exemplo - são removidos. Em contraste, os outliers que não são causados por erros e que revelam informações ou tendências novas e imprevistas geralmente são não deletado.

10. Compreender a importância de (às vezes) reter outliers. Embora alguns outliers devam ser removidos de um conjunto de dados porque são o resultado de erros ou porque distorcem os resultados de forma enganosa, outros outliers devem ser preservados. Por exemplo, se um outlier foi obtido corretamente (ou seja, não o resultado de um erro) e/ou se o outlier fornece uma nova visão sobre o fenômeno a ser medido, ele não deve ser removido imediatamente. Experimentos científicos são situações particularmente sensíveis quando se trata de lidar com discrepâncias – remover erroneamente uma discrepância pode significar descartar informações importantes sobre uma nova tendência ou descoberta.
Pontas
- Se você encontrar discrepâncias, tente explicá-las antes de removê-las do conjunto de dados; eles podem indicar erros de medição ou desvios na distribuição.
Necessidades
- Calculadora
Artigos sobre o tópico "Calcular valores atípicos"
Оцените, пожалуйста статью
Popular