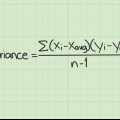Calculando o Tamanho da Amostra: 14 Passos (com Imagens)

Contente

Degraus

Os estudos científicos geralmente se baseiam em pesquisas realizadas entre uma pequena proporção de uma população total. No entanto, sua amostra precisará ter um número mínimo de pontos de dados se você quiser que ela represente com precisão as condições da população total que pretende representar. Para calcular o tamanho da amostra necessário, você precisa determinar alguns valores fixos e inseri-los em uma fórmula apropriada.

Degraus

Parte 1 de 4: Determinando os valores mais importantes

Imagem intitulada Calcular o tamanho da amostra Etapa 1

1. Conheça o tamanho da sua população. O tamanho da população refere-se ao número total de pontos de dados em sua população. Para estudos maiores, você pode usar um valor estimado em vez do número exato.

A precisão tem um impacto estatístico maior quando você trabalha com um grupo menor. Por exemplo, se você deseja pesquisar membros de uma organização ou funcionários de uma pequena empresa, o tamanho da população deve ser preciso para uma dúzia de pessoas.
Pesquisas maiores permitem maior desvio da população real. Por exemplo, se sua demografia inclui todos os que vivem na Holanda, você pode estimar o tamanho em aproximadamente 17 milhões de pessoas, mesmo que o valor real possa diferir em centenas de milhares.

Imagem intitulada Calcular o tamanho da amostra Etapa 2

2. Determine sua margem de erro. A margem de erro, também conhecida como "intervalo de confiança", refere-se a quanta variação você deseja permitir em seus resultados.

A margem de erro é uma porcentagem que indica quão próximos os resultados de sua amostra estarão do valor real da população total discutida em seu estudo.

Uma margem de erro menor resultará em respostas mais precisas, mas escolher uma margem de erro menor também exigirá uma amostra maior.

Quando os resultados de uma pesquisa são apresentados, a margem de erro geralmente aparece como uma porcentagem mais ou menos. Por exemplo: `35% das pessoas concordam com opção A, com margem de erro de +/- 5%`

Neste exemplo, a margem de erro indica essencialmente que, se toda a população recebesse a mesma pergunta da pesquisa, você tem "certeza" de que algo entre 30% (35 - 5) e 40% (35 + 5) concordaria em opção A.

Imagem intitulada Calcular o tamanho da amostra Etapa 3

3. Determine seu nível de confiança. O nível de confiança está intimamente relacionado ao intervalo de confiança (margem de erro). Esse valor mede seu grau de certeza sobre o quão bem uma amostra representa a população total dentro da margem de erro escolhida.

Em outras palavras, se você escolher um nível de confiança de 95%, poderá afirmar que está 95% confiante de que seus resultados estão dentro da margem de erro escolhida.

Um nível de confiança mais alto indica um maior grau de precisão, mas também requer uma amostra maior. Os níveis de confiança mais comuns são 90% de certeza, 95% de certeza e 99% de certeza.

Definir um nível de confiança de 95% para o exemplo dado na etapa de margem de erro significa que você está 95% confiante de que 30% a 40% do total da população afetada concorda com a `opção A` de sua pesquisa.

Imagem intitulada Calcular o tamanho da amostra Etapa 4

4. Especifique seu desvio padrão. O desvio padrão indica quanta variação você espera entre suas respostas.

Respostas extremas são mais prováveis de serem precisas do que resultados moderados.

Se 99% das respostas à sua pesquisa responderem `Sim` e apenas 1% `Não`, a amostra provavelmente será um reflexo muito preciso de toda a população.

Por outro lado, se 45% responder `Sim` e 55% `Não`, há maior chance de erro.

Como esse valor é difícil de determinar ao fornecer a pesquisa real, a maioria dos pesquisadores define esse valor em 0,5 (50%). Essa é a porcentagem do pior caso, portanto, manter esse valor garantirá que o tamanho da amostra calculada seja grande o suficiente para representar com precisão a população total dentro do seu intervalo de confiança e nível de confiança.

Imagem intitulada Calcular o tamanho da amostra Etapa 5

5. Encontre o seu Z-score. O Z-score é um valor constante que é definido automaticamente com base no seu nível de confiança. Indica a `pontuação normal padrão`, ou o número de desvios padrão entre um valor selecionado e a média da população.

Você pode calcular os z-scores manualmente, usar uma calculadora online ou encontrar seu z-score em uma tabela de z-scores. No entanto, cada um desses métodos pode ser bastante complexo.

Como os níveis de confiança são bastante padronizados, a maioria dos pesquisadores simplesmente lembra o z-score necessário para os níveis de confiança mais comuns:

80% de confiabilidade => 1,28 pontuação z

85% de confiabilidade => 1,44 pontuação z

90% de confiabilidade => 1,65 pontuação z

95% de confiança => pontuação z de 1,96

99% de confiabilidade => 2,58 pontuação z

Parte 2 de 4: Usando a fórmula padrão

Imagem intitulada Calcular o tamanho da amostra Etapa 6

1. Veja a comparação. Se você tem uma população pequena a média e conhece todos os valores-chave, deve usar a fórmula padrão. A fórmula padrão para um tamanho de amostra é:

Tamanho da amostra =*p(1-p)] / e / _{1 + [z *p(1-p)] / e *N}]

N = tamanho da população
z = pontuação z
e = margem de erro
p = desvio padrão

Imagem intitulada Calcular o tamanho da amostra Etapa 7

2. Insira seus valores. Substitua as variáveis pelos valores numéricos que realmente se aplicam à sua pesquisa específica.

Exemplo: Determine o tamanho ideal do estudo para uma população de 425 indivíduos. Use um nível de confiança de 99%, um desvio padrão de 50% e uma margem de erro de 5%.

Para 99% de confiança, você deve ter um z-score de 2,58.

Isso significa que:

N = 425

z = 2,58

e = 0,05

p = 0,5

Imagem intitulada Calcular o tamanho da amostra Etapa 8

3. Faça o cálculo. Resolva a equação com os novos números inseridos. A solução é o tamanho de amostra necessário.

Exemplo: Tamanho da amostra =*p(1-p)] / e / _{1 + [z *p(1-p)] / e *N]}

=*0,5(1-0,5)] / 0,05 / _{1 + [2,58 *0,5(1-0.5)] / 0,05 *425]}

=/ _{1 + [6,6564 *0,25] / 1,0625]}

= 665 / 2,5663

= 259,39(responder)

Parte 3 de 4: Configurando uma fórmula para populações desconhecidas ou muito grandes

Imagem intitulada Calcular o tamanho da amostra Etapa 9

1. Examinar a fórmula. Se você tiver uma população desconhecida ou muito grande, precisará usar uma segunda fórmula. Se ainda houver valores para o restante das variáveis, use a seguinte equação:

Tamanho da amostra = [z *p(1-p)] / e

z = pontuação z
e = margem de erro
p = desvio padrão

Saiba que esta equação é apenas a metade superior da fórmula completa.

Imagem intitulada Calcular o tamanho da amostra Etapa 10

2. Preencha a equação com seus valores. Substitua cada variável pelos valores numéricos escolhidos para sua pesquisa.

Exemplo: Determine o tamanho de estudo necessário para uma população desconhecida com um nível de confiança de 90%, um desvio padrão de 50% e uma margem de erro de 3%.

Para 90% de confiança, o z-score seria 1,65.

Isso significa que:

z = 1,65

e = 0,03

p = 0,5

Imagem intitulada Calcular o tamanho da amostra Etapa 11

3. Faça o cálculo. Depois de colocar seus números na fórmula, resolva a equação. Sua resposta indicará o tamanho da amostra necessária.

Exemplo: Tamanho da amostra = [z *p(1-p)] / e

= [1,65 *0,5(1-0,5)] / 0,03

= [2,7225 *0,25] / 0,0009

= 0,6806 / 0,0009

= 756,22 (responder)

Parte 4 de 4: Usando a fórmula de Slovin

Imagem intitulada Calcular o tamanho da amostra Etapa 12

1. Veja a fórmula. A fórmula de Slovin é uma equação muito geral usada quando você pode estimar a população, mas não tem ideia de como uma determinada população se comporta. A fórmula é descrita a seguir:

Tamanho da amostra = N / (1 + N*e)

N = população
e = margem de erro

Saiba que esta é a fórmula menos precisa e, como tal, a menos ideal. Você só deve usá-lo se as circunstâncias o impedirem de determinar um desvio padrão apropriado e/ou nível de confiança (o que também o impede de determinar seu z-score).

Imagem intitulada Calcular o tamanho da amostra Etapa 13

2. Insira os valores. Substitua cada variável pelos valores numéricos específicos da sua pesquisa.

Exemplo: Calcule o tamanho do estudo necessário para uma população de 240 indivíduos, levando em consideração uma margem de erro de 4%.

Isso significa que:

N = 240

e = 0,04

Imagem intitulada Calcular o tamanho da amostra Etapa 14

3. Faça o cálculo. Resolva a equação usando os números específicos para sua pesquisa. A resposta que você encontrar deve ser o tamanho de sua pesquisa.

Exemplo: Tamanho da amostra = N / (1 + N*e)

= 240 / (1 + 240 *0,04)

= 240 / (1 + 240 *0,0016)

= 240 / (1 + 0,384}

= 240 / (1.384)

= 173,41 (responder)