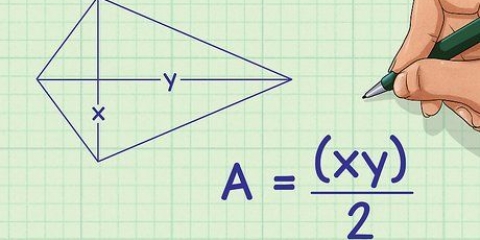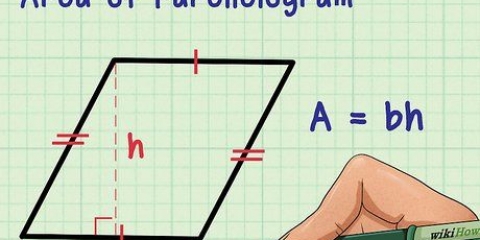Instruções gratuitas passo a passo 
Área = 1/2 x (3cm x 5cm) 
Área = 1/2 x (3cm x 5cm) Superfície = 1/2 x 15 cm Área = 7.5 cm 
Área = √{6 (6 - 3)(6 - 4)(6 - 5)} 
6 - 3 = 3 6 - 4 = 2 6 - 5 = 1 Área = √{6 (3)(2)(1)} 
Área = 1/2(b)(c) x sen A Área = 1/2(150)(231) x sen A 
Área = 1/2(150)(231) x sen A Área = 1/2(34.650) x sen A Área = 17,325 x sen A Área = 17.325 x .8386705 Área = 14,530 cm
Calcular a área de um triângulo
Contente
Embora o método mais comum de calcular a área de um triângulo seja multiplicar sua meia base por sua altura, existem várias outras maneiras de calcular a área de um triângulo, dependendo dos dados disponíveis. Isso inclui o comprimento de todos os três lados, o comprimento de um lado de um triângulo equilátero e o comprimento de dois lados junto com o ângulo incluído. Leia aqui como você pode calcular a área de um triângulo usando esses dados.
Degraus
Método 1 de 4: Com a base e a altura
1. Determine a base e a altura do seu triângulo. A base do triângulo é o comprimento de um lado, que geralmente é o lado inferior do triângulo. Altura é o comprimento da base ao canto superior do triângulo, que é perpendicular à base. Em um triângulo retângulo, a base e a altura são os dois lados que se encontram em um ângulo de 90 graus. Mas, em outro triângulo, como visto abaixo, a linha de altitude cortará a forma.
- Depois de determinar a base e a altura do triângulo, você está pronto para começar a usar a fórmula.
2. Anote a fórmula para encontrar a área de um triângulo. A fórmula para este tipo de problema é Área = 1/2 (base x altura), ou 1/2 (sutiã). Depois de anotar tudo, você pode começar a preencher o comprimento da altura e da base.
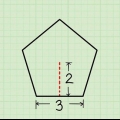
3. Insira os valores de base e altura. Encontre a base e a altura do triângulo e use esses valores na equação. Neste exemplo, a altura do triângulo é 3 cm e a base do triângulo é 5 cm. Esta é a aparência da fórmula depois de inserir esses valores:
4. Resolva a equação. Você pode multiplicar a altura pela base primeiro porque esses valores estão entre parênteses. Então você multiplica o resultado por 1/2. Lembre-se que você dará a resposta em metros quadrados porque está trabalhando em um espaço bidimensional. Veja como resolver isso para a resposta final:
Método 2 de 4: Usando o comprimento de cada lado (Fórmula de Heron)
1. Calcule o meio perímetro (semiperímetro) do triângulo. Para encontrar a metade do perímetro do triângulo tudo o que você precisa fazer é somar todos os lados e dividir o resultado por dois. A fórmula para encontrar o meio perímetro de um triângulo é a seguinte: semiperímetro = (comprimento do lado a + comprimento do lado b + comprimento do lado c) / 2, ou s = (a + b + c) / 2. Como todos os três comprimentos do triângulo retângulo são dados, 3 cm, 4 cm e 5 cm, você pode colocá-los diretamente nas fórmulas e resolver o problema para o meio perímetro:
- s = (3 + 4 + 5)/2
- s = 12/2
- s = 6
2. Digite os valores corretos na fórmula para encontrar a área de um triângulo. Esta fórmula para encontrar a área de um triângulo também é chamada de fórmula de Heron e é assim: Área = √{s (s - a)(s - b)(s - c)}. Repetimos o passo anterior onde s a meia circunferência é e uma, b, e c os três lados do triângulo. Faça uso da seguinte sequência de operações: comece resolvendo tudo dentro dos parênteses, depois tudo sob o sinal de radical e, finalmente, a própria raiz quadrada. Veja como ficará essa fórmula quando você inserir todos os valores conhecidos:
3. Subtraia os valores dentro dos parênteses. Então: 6 - 3, 6 - 4 e 6 - 5. Aqui está o resultado no papel:
4. Multiplique os resultados dessas operações. Multiplique 3 x 2 x 1 para obter 6 como resposta. Você tem que multiplicar esses números antes de multiplicá-los por 6 porque eles estão entre parênteses.
5. Multiplique o resultado anterior pela metade da circunferência. Em seguida, multiplique o resultado, 6, pela meia circunferência, que também é 6. 6 x 6 = 36.
6. Calcule a raiz quadrada. 36 é um quadrado perfeito e √36 = 6. Não se esqueça da unidade com a qual você começou - centímetros. Expresse a resposta final em centímetros quadrados. A área do triângulo com lados 3, 4 e 5 é 6 cm.
Método 3 de 4: Usando um lado de um triângulo retangular
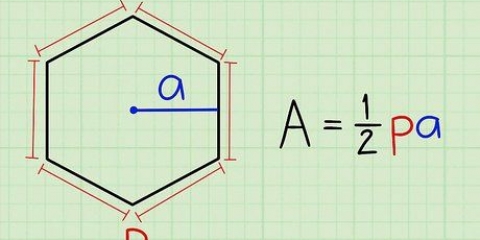
1. Encontre o lado do triângulo equilátero. Um triângulo equilátero tem lados de igual comprimento e ângulos iguais. Você sabe que está lidando com um triângulo equilátero, seja porque é um dado, ou porque sabe que todos os ângulos e todos os lados têm o mesmo valor. O valor de um dos lados desse triângulo é 6 cm. Observe isso.
- Se você sabe que está lidando com um triângulo equilátero, mas apenas o perímetro é conhecido, basta dividir esse valor por 3. Por exemplo, o comprimento de um lado de um triângulo equilátero com perímetro 9 é simplesmente 9/3, ou 3.
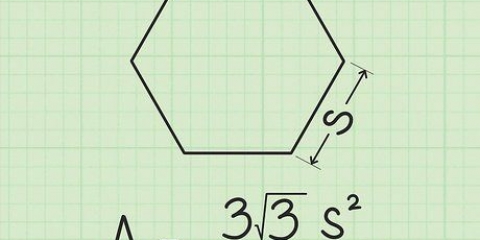
2. Escreva a fórmula para encontrar a área de um triângulo equilátero. A fórmula para este tipo de problema é área = (s^2)(√3)/4. Observe que s “seda” significa.
3. Aplicar o valor de um lado à equação. Primeiro calcule o quadrado do lado com valor 6, para obter 36. Em seguida, encontre o valor de √3, se a resposta for dada em decimais. Agora digite √3 em sua calculadora para obter 1.732 para obter. Divida este número por 4. Observe que você também pode dividir 36 por 4 e depois multiplicar por √3 -- a ordem das operações não afeta a resposta.
4. Resolver. Agora se resume principalmente a apenas contar. 36 x √3/4 = 36 x .433 = 15.59 cm A área de um triângulo equilátero com um lado de 6 cm de comprimento é 15.59 centímetros.
Método 4 de 4: usando o comprimento de dois lados e o ângulo incluído
1. Encontre o valor dos comprimentos de dois lados e o ângulo incluído. O ângulo incluído é o ângulo entre os dois lados conhecidos do triângulo. Você precisa conhecer esses valores para encontrar a área de um triângulo usando este método. Vamos supor um triângulo com as seguintes dimensões:
- ângulo A = 123º
- lado b = 150 cm
- lado c = 231 cm
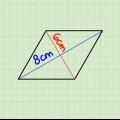
2. Anote a fórmula para encontrar a área do triângulo. A fórmula para encontrar a área de um triângulo com dois lados conhecidos e um ângulo incluído conhecido é a seguinte: Área = 1/2(b)(c) x sen A. Nesta equação represente "b" e "c" os comprimentos dos lados e "uma" a esquina. Você deve sempre tomar o seno do ângulo nesta equação.
3. Preencha os valores na equação. Veja como fica a equação depois de inserir esses valores:
4. Resolver. Para resolver esta equação, primeiro multiplique os lados e divida o resultado por dois. Em seguida, multiplique esse resultado pelo seno do ângulo. O valor do seno pode ser encontrado com sua calculadora. Não se esqueça de dar sua resposta em unidades cúbicas. Veja como fazer isso:
Pontas
- Se você não entende por que a fórmula básica de altura funciona dessa maneira, aqui está uma breve explicação. Se você fizer um segundo triângulo idêntico e colocá-lo um ao lado do outro, ele forma um retângulo (dois triângulos retângulos) ou um paralelogramo (dois triângulos não retângulos). Para encontrar a área de um retângulo ou paralelogramo tudo que você precisa fazer é multiplicar a base pela altura. Como um triângulo é igual a meio retângulo ou paralelogramo, segue-se que a área de um triângulo é igual a meia base vezes sua altura.
Artigos sobre o tópico "Calcular a área de um triângulo"
Оцените, пожалуйста статью
Popular
