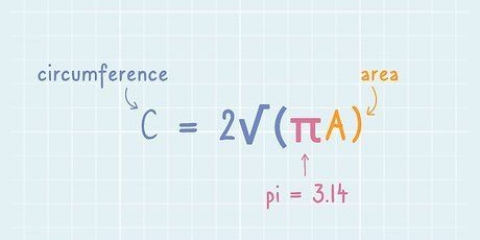Por exemplo, suponha que o ângulo central seja 100 graus, então você divide 100 por 360 e, assim, obtém 0,28. Portanto, a área do segmento é cerca de 28% da área de todo o círculo. Se você não conhece o ângulo central, mas sabe que parte do círculo é o segmento, encontre o ângulo multiplicando essa fração por 360. Por exemplo, se você sabe que o segmento é um quarto do círculo, multiplique 360 por um quarto (0,25) para obter 90 graus. 
Por exemplo, se o raio for 5 cm, você calcularia 5 x 5 = 25, e então 25 x 3,14 = 78,5. Se você não sabe o comprimento do raio, mas sabe o diâmetro, divida o diâmetro por dois para encontrar o raio. 
Por exemplo: 0,28 x 78,5 = 21,89. Como você está calculando a área, sua resposta deve ser expressa em centímetros quadrados.. 

Por exemplo, se o comprimento do arco for 5cm e o raio for 8cm, seu novo contador será 40. 
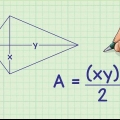
Por exemplo:  .
. Como você está calculando a área, sua resposta deve ser expressa em centímetros quadrados.
Calcular a área de um segmento
Contente
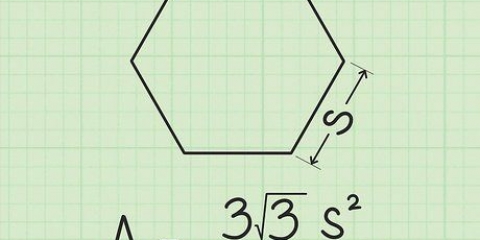
Às vezes é necessário determinar a área sob um arco ou a área de um segmento. Um segmento é uma parte de um círculo que tem a forma de uma fatia de pizza ou torta. Para encontrar a área desta peça, você precisa saber o comprimento do raio do círculo. Além do raio, você precisa saber o ângulo central em graus ou o comprimento do arco. Com essas medidas, determinar a área de um segmento é uma simples questão de preencher os números em fórmulas fixas.
Degraus
Método 1 de 2: Calcule a área cujo ângulo central e raio são conhecidos

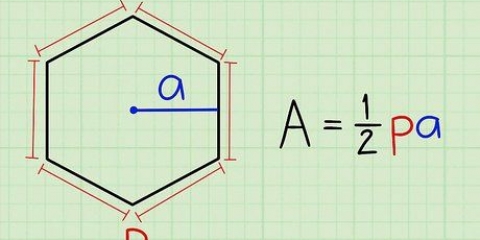
1. Monte a fórmula: . Na fórmula, r é o raio e θ é o número de graus do ângulo central do segmento.
. Na fórmula, r é o raio e θ é o número de graus do ângulo central do segmento.
 . Na fórmula, r é o raio e θ é o número de graus do ângulo central do segmento.
. Na fórmula, r é o raio e θ é o número de graus do ângulo central do segmento. - Lembre-se que a área de um círculo é igual a
. Ao determinar a área de um segmento, você está apenas calculando a área do círculo inteiro, multiplicando isso pela fração do círculo que o segmento representa.
- Um círculo tem 360 graus, então se você colocar o ângulo central do segmento acima de 360 como uma fração, você obtém a parte de todo o círculo.

2. Insira o ângulo central do segmento na fórmula. Divida o ângulo central por 360. Fazer isso lhe dará a parte ou porcentagem de todo o círculo que o segmento representa.

3. Insira o raio na fórmula. Eleve o raio ao quadrado e multiplique a resposta por 𝝅 (3.14). Calcula a área de todo o círculo.

4. Multiplique os dois números juntos. Você multiplica a porcentagem novamente pela área de todo o círculo. Isso lhe dará a área do segmento.
Método 2 de 2: Calcule a área com comprimento e raio de arco conhecidos

1. Monte a fórmula: . Na fórmula, r é o comprimento do raio e l = o comprimento do arco.
. Na fórmula, r é o comprimento do raio e l = o comprimento do arco.
 . Na fórmula, r é o comprimento do raio e l = o comprimento do arco.
. Na fórmula, r é o comprimento do raio e l = o comprimento do arco. - Use a fórmula para encontrar a circunferência de um círculo: 2r. Se você conhece o comprimento do arco (que é parte da circunferência), pode determinar qual parte do círculo o segmento representa comparando o comprimento do arco com a circunferência total.
- A fórmula completa é então:
-- no entanto, você pode simplificar isso para
.

2. Insira o comprimento do arco e o raio na fórmula. Você vai multiplicar esses dois números para obter um novo contador.

3. Dividir por dois. Você divide o contador que você encontra na etapa dois. Isso lhe dará a área do segmento.
 .
.Artigos sobre o tópico "Calcular a área de um segmento"
Оцените, пожалуйста статью
Popular