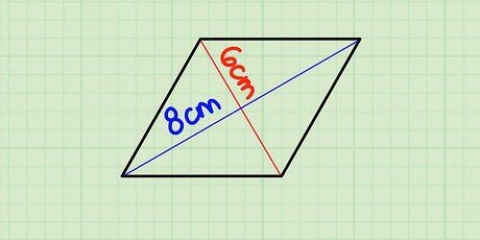
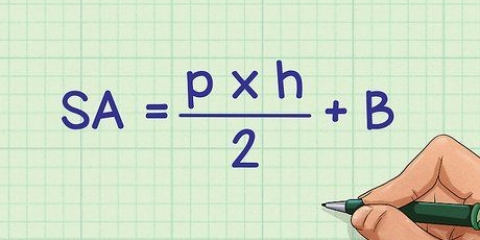Por exemplo, se uma pipa tem duas diagonais de 7 cm e 10 cm, sua fórmula ficaria assim: .
. 
Por exemplo:



Por exemplo:


A área de uma pipa com diagonais de 10 cm e 7 cm é, portanto, 35 cm quadrados. 

Por exemplo, se sua pipa tiver 20cm de lado e 15cm de lado, sua fórmula ficará assim:  .
. 
Por exemplo:



Por exemplo: se o ângulo  então sua fórmula ficará assim:
então sua fórmula ficará assim:  .
. 
Por exemplo, o seno de um ângulo de 150 graus é 0,5, então sua fórmula ficará assim:  .
. 
Por exemplo:


Assim, a superfície de uma pipa, com dois lados de 20 cm e 15 cm, e o ângulo entre eles de 150 graus, é de 150 cm quadrados. 

Por exemplo, se sua pipa tiver uma área de 35 cm quadrados, sua fórmula ficará assim:  .
. 
Por exemplo, se você sabe que uma das diagonais tem 7 cm de comprimento, sua fórmula ficará assim:  .
. 
Por exemplo:




Por exemplo:



O comprimento da diagonal em falta de uma pipa, dada uma área de 35 cm quadrados e uma diagonal de 7 cm, é, portanto, 10 cm.
Calcular a área de uma pipa
Contente
Uma pipa é um tipo de quadrilátero com dois pares de lados iguais e adjacentes. As pipas podem ter a aparência tradicional de uma pipa, mas uma pipa também pode ser um diamante ou um quadrado. Não importa a aparência de uma pipa, os métodos para encontrar a superfície serão os mesmos. Se você conhece o comprimento das diagonais, pode encontrar a área através de matemática simples. Você também pode usar a trigonometria para encontrar a área, se souber os lados e os ângulos da figura.
Degraus
Método 1 de 3: Usando as diagonais para determinar a área

1. Escreva a fórmula para a área de uma pipa, dadas duas diagonais. A fórmula é  , através do qual
, através do qual  é igual à área da pipa, e
é igual à área da pipa, e  e
e  é igual ao comprimento das diagonais da pipa.
é igual ao comprimento das diagonais da pipa.
 , através do qual
, através do qual  é igual à área da pipa, e
é igual à área da pipa, e  e
e  é igual ao comprimento das diagonais da pipa.
é igual ao comprimento das diagonais da pipa.
2. Aplique os comprimentos das diagonais à fórmula. Uma diagonal é uma linha reta que vai de um vértice ao vértice do outro lado. Você deve obter o comprimento das diagonais ou ser capaz de medi-las. Se você não sabe o comprimento das diagonais, não pode usar este método.
 .
.
3. Multiplique os comprimentos das diagonais. O produto se torna o novo balcão na comparação de área.



4. Divida o produto das diagonais por 2. Isso lhe dará a área da pipa, em unidades quadradas.


A área de uma pipa com diagonais de 10 cm e 7 cm é, portanto, 35 cm quadrados.
Método 2 de 3: Usando um ângulo e dois lados para determinar a área

1. Escreva a fórmula para a superfície da pipa. Esta fórmula funciona se você conhece dois lados não conformes e o tamanho do ângulo entre esses dois lados. A fórmula é  , através do qual
, através do qual  é igual a área da pipa,
é igual a área da pipa,  e
e  é igual aos lados desiguais da pipa, e
é igual aos lados desiguais da pipa, e  é igual ao ângulo entre os lados
é igual ao ângulo entre os lados e
e  .
.
 , através do qual
, através do qual  é igual a área da pipa,
é igual a área da pipa,  e
e  é igual aos lados desiguais da pipa, e
é igual aos lados desiguais da pipa, e  é igual ao ângulo entre os lados
é igual ao ângulo entre os lados e
e  .
. - Verifique se você tem dois lados desiguais. Uma pipa tem dois pares de lados congruentes. Você deve usar um lado de cada par. Certifique-se de começar do ângulo entre esses dois lados. Se você não tiver todas essas informações, não poderá usar este método.

2. Aplique o comprimento dos lados à fórmula. Esta informação deve ser fornecida, caso contrário você deve ser capaz de medi-la. Lembre-se de que você está usando lados não congruentes, então cada lado tem um comprimento diferente.
 .
.
3. Multiplique os lados juntos. Aplique este produto na fórmula.



4. Aplique o ângulo à fórmula. Certifique-se de usar o ângulo entre os dois lados não congruentes.
 então sua fórmula ficará assim:
então sua fórmula ficará assim:  .
.
5. Determine o seno do ângulo. Para isso, você pode usar uma calculadora ou uma tabela trigonométrica.
 .
.
6. Multiplique o produto dos lados pelo seno do ângulo. Este resultado é a área da pipa, em unidades quadradas.


Assim, a superfície de uma pipa, com dois lados de 20 cm e 15 cm, e o ângulo entre eles de 150 graus, é de 150 cm quadrados.
Método 3 de 3: Usando a área para encontrar uma diagonal ausente

1. Escreva a fórmula para a área de uma pipa, dadas duas diagonais. A fórmula é  , através do qual
, através do qual  é igual à área da pipa, e
é igual à área da pipa, e  e
e  é igual ao comprimento das diagonais da pipa.
é igual ao comprimento das diagonais da pipa.
 , através do qual
, através do qual  é igual à área da pipa, e
é igual à área da pipa, e  e
e  é igual ao comprimento das diagonais da pipa.
é igual ao comprimento das diagonais da pipa.
2. Aplique a área da pipa na fórmula. Esta informação deve ser dada. Assegure-se de que você  substitui.
substitui.
 substitui.
substitui. .
.
3. aplique o comprimento da diagonal conhecida à fórmula. substituir  .
.
 .
. .
.
4. Multiplique cada lado da equação por 2. Isso removerá a fração na fórmula.




5. Divida cada lado da equação pelo comprimento da diagonal. Isso lhe dará o comprimento da diagonal ausente.



O comprimento da diagonal em falta de uma pipa, dada uma área de 35 cm quadrados e uma diagonal de 7 cm, é, portanto, 10 cm.
Necessidades
- Calculadora (opcional)
- Régua (opcional)
- Lápis (opcional)
- Papel (opcional)
Artigos sobre o tópico "Calcular a área de uma pipa"
Оцените, пожалуйста статью
Popular