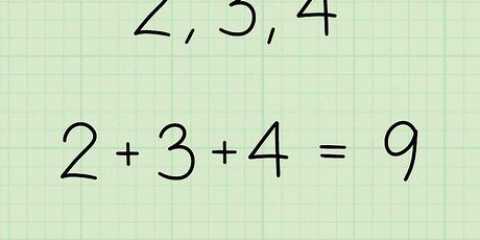Determinando o intervalo interquartil

Contente

Degraus
Pontas

O intervalo interquartil é usado para calcular a dispersão de um conjunto de dados. O intervalo interquartil é usado em análises estatísticas para tirar conclusões sobre um conjunto de dados. Muitas vezes, é preferível calcular o intervalo interquartil em vez do intervalo, porque a maioria dos valores discrepantes não é incluída. Continue lendo para descobrir como determinar o intervalo interquartil.

Degraus

Método 1 de 3: Entendendo o intervalo interquartil

Imagem intitulada Encontre o IQR Passo 1

1. Entenda como o intervalo interquartil é usado. É essencialmente uma maneira de entender a distribuição de um conjunto de dados. O intervalo interquartil é a diferença entre o quartil mais alto (os 25%) mais altos e o quartil mais baixo (os 25%) mais baixos de um conjunto de dados. O quartil mais baixo é geralmente marcado com Q1 e o quartil mais alto com Q3, teoricamente tornando Q2 o centro do conjunto de dados e Q4 o ponto mais alto.

Imagem intitulada Encontre o IQR Passo 2

2. Entenda o que são quartis. Para visualizar um quartil, divida uma lista de números em quatro partes iguais. Cada uma dessas partes é um "quartil." Dê uma olhada no seguinte conjunto de dados: 1, 2, 3, 4, 5, 6, 7, 8.

1 e 2 formam o primeiro quartil, ou Q1.

3 e 4 formam o segundo quartil, ou Q2.

5 e 6 formam o terceiro quartil, ou Q3.

7 e 8 formam o quarto quartil, ou Q4.

Imagem intitulada Encontre o IQR Passo 3

3. Aprenda a fórmula. Para encontrar a diferença entre o quartil mais alto e o mais baixo, subtraia o percentil 75 do percentil 25. A fórmula é escrita da seguinte forma: Q3 – Q1 = intervalo interquartil.

Método 2 de 3: Organize a coleta de dados

Imagem intitulada Encontre o IQR Passo 4

1. Colete seus dados. Se você tiver que aprender isso para a escola e fazer um teste, provavelmente obterá um conjunto de dados prontos, como 1, 4, 5, 7, 10. Este é o seu conjunto de dados ou os números com os quais você trabalhará. No entanto, você pode ter que organizar os números com base em uma tabela ou uma soma de histórias. Certifique-se de que cada número se refere à mesma coisa, por exemplo, o número de ovos em cada ninho dentro de um grupo de pássaros ou o número de vagas de estacionamento que cada casa tem em uma determinada rua.

2. Classifique seu conjunto de dados em ordem crescente. Isso significa que você ordena os dados do menor para o maior número. Dê uma olhada nos exemplos a seguir:

Exemplo com um número par de números (conjunto A): 4 7 9 11 12 20

Exemplo com um número ímpar de números (conjunto B): 5 8 10 10 15 18 23

3. Divida os dados ao meio. Para fazer isso, você precisa determinar o centro dos dados: o número ou números que estão exatamente no meio do conjunto de dados. Se você tiver um número ímpar de números, escolha o número que está exatamente no meio. Se você tiver um número par de números, o ponto médio estará entre os dois números do meio.

Exemplo com número par de números (conjunto A), em que o ponto médio está entre 9 e 11: 4 7 9 | 11 12 20

Exemplo com um número ímpar de números (conjunto B), onde (10) é o centro: 5 8 10 (10) 15 18 23

Método 3 de 3: Calculando o intervalo interquartil

1. Determine a mediana da metade inferior e superior do seu conjunto de dados. A mediana é a "Centro," ou o número no meio de um conjunto de dados. Nesse caso, você não está procurando o centro de todo o conjunto de dados, mas o centro relativo das metades superior e inferior. Se você tiver um número ímpar de números, não inclua o ponto médio. Por exemplo, no conjunto de dados B você não incluiria uma das dezenas.

Exemplo com um número par de números (conjunto A):

Mediana da metade inferior = 7 (Q1)
Metade superior mediana = 12 (3º trimestre)

Exemplo com um número ímpar de números (conjunto B):

Mediana da metade inferior = 8 (Q1)

Metade superior mediana = 18 (3º trimestre)

2. Resolva Q3 - Q1 para determinar o intervalo interquartil. Agora você sabe quantos números estão entre os percentis 25 e 75. Você pode usar isso para entender a dispersão dos dados. Por exemplo, se você pode obter um máximo de 100 pontos em um teste e o intervalo interquartil das notas obtidas é 5, então você pode supor que a maioria das pessoas que fizeram este teste sabiam sobre a mesma quantidade do assunto. Não há muita diferença entre os números altos e baixos. No entanto, se o intervalo interquartil das notas obtidas for 30, você pode se perguntar por que algumas pessoas tiveram uma nota tão alta e outras tão baixa.

Exemplo com um número par de números (conjunto A): 12 - 7 = 5

Exemplo com um número ímpar de números (conjunto B): 18 - 8 = 10

Pontas

É importante aprender a calcular isso sozinho, mas há várias calculadoras on-line que você pode usar para verificar se calculou o intervalo interquartil corretamente. Não confie muito em um aplicativo de calculadora se você tiver que aprender isso para a aula de matemática na escola. Se for perguntado sobre o intervalo interquartil em um teste, você terá que calcular isso de cor.