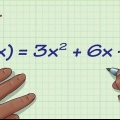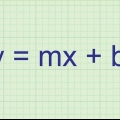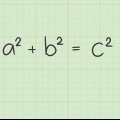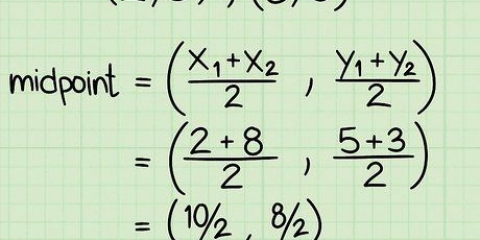Determinando um derivado

1. Entenda a notação de uma derivada. As duas formas de notação a seguir são as mais comuns, mas várias outras maneiras podem ser encontradas em Wikipédia.

• Notação de Leibniz Esta notação é mais comumente usada quando a equação contém ay e x. Dy/dx significa literalmente "a derivada de y em relação a x". Tente pensar nisso como Δy/Δx para os valores de x e y onde a diferença é infinitesimal. Esta explicação dá naturalmente a definição de um limite em relação à derivada: lim_h->0 (f(x+h)-f(x))/h. Aplicando esta notação à segunda derivada, escreva: dy/dx.
• Notação de Lagrange A derivada de uma função f também é escrita como f`(x). Esta notação é pronunciada como "a função f de x". Esta notação é mais curta que a de Leibniz e é usada quando se considera uma derivada como uma função. Para derivadas mais altas, basta adicionar outro " ` " Pronto para "f", fazendo a segunda derivada parecer f``(x).

2. Entenda o que é um derivado e para que serve. Primeiro, para encontrar a inclinação de um gráfico linear, dois pontos na linha são tomados e essas coordenadas são inseridas na equação (y₂ - y₁)/(X₂ - X₁). Mas, isso só é possível com gráficos lineares. Para equações quadráticas e acima, o gráfico é uma curva, então a diferença entre dois pontos não é suficientemente precisa. Para encontrar a inclinação de uma tangente de uma parábola, dois pontos são tomados e preenchidos na equação, para determinar a inclinação de uma linha curva: [f(x + dx) - f(x)]/dx. Dx significa"delta x," qual é a diferença entre as duas coordenadas x dos dois pontos do gráfico. Observe que esta equação é a mesma que (y₂ - y₁)/(X₂ - X₁), mas de uma forma diferente. Como já se sabe que o resultado não será preciso, uma aproximação indireta é escolhida. Para encontrar a inclinação da tangente no ponto (x, f(x)), dx deve se aproximar de 0 para que os dois pontos escolhidos sejam quase os mesmos.Mas você não pode dividir por 0, então depois de preencher os valores dos dois pontos você tem que eliminar dedx no denominador. Se isso for bem sucedido, faça dx igual a 0 e resolva. Esta é a inclinação da tangente em (x, f(x)). A derivada de uma equação é a equação geral para encontrar a inclinação de qualquer tangente de um gráfico. Isso pode parecer muito difícil, mas os exemplos abaixo mostrarão como determinar a derivada.

1. Use a diferenciação explícita se y já estiver em um lado da equação.

2. Substituir uma equação em outra equação [f(x + dx) - f(x)]/dx. Por exemplo, a equação y = x, cuja derivada é [(x + dx) - x]/dx.

3. Expanda dx ainda mais para obter a equação [dx(2x + dx)]/dx. Agora é possível eliminar o dx no numerador e denominador. O resultado é 2x + dx, e quando dx se aproxima de 0 a derivada se torna 2x. Esta é a inclinação de qualquer tangente ao gráfico y = x é 2x. Basta digitar o valor de um determinado ponto x que você deseja encontrar a tangente na equação.

4. Aprenda a reconhecer os padrões do mesmo tipo de equações. Abaixo você encontrará alguns.

1. Use a diferenciação implícita quando sua equação não puder ser simplesmente escrita com o y de um lado do sinal de igual. Mesmo se você escrever com o y de um lado, calcular dy/dx ainda seria uma tarefa árdua. Abaixo está um exemplo de como resolver este tipo de equação.

2. Neste exemplo, xy + 2y = 3x + 2y, substitua jey por f(x), para que fique claro que esta é realmente uma função. A equação então se torna xf(x) + 2[f(x)] = 3x + 2f(x).

3. Para encontrar a derivada desta equação, diferencie (uma palavra impressionante para encontrar a derivada) seus dois lados da equação em relação a x. A equação então se torna xf`(x) + 2xf(x) + 6[f(x)]f`(x) = 3 + 2f`(x).

4. Substitua f(x) novamente por y. Tenha cuidado para não fazer isso com f`(x), pois isso é muito diferente de f(x).

5. Resolva para f`(x). A resposta deste exemplo é (3 - 2xy)/(x + 6y - 2).

1. Tirar a derivada mais alta de uma função significa apenas tirar a derivada da derivada. Por exemplo, se a terceira derivada for solicitada, você pega a derivada da derivada da derivada. Para algumas equações, uma derivada mais alta se torna igual a 0.

1. Se y é uma função diferenciável de z, e z é uma função diferenciável de x, então y é uma função composta de x, e a derivada de y em relação a x (dy/dx) é (dy/du)*(du /dx). A regra da cadeia também pode ser uma equação composta, assim: (2x - x). Para encontrar a derivada disso; apenas pense da mesma maneira que você faz com a linha de produtos. Multiplique a equação pelo expoente e reduza o expoente por 1. Em seguida, multiplique a equação pela derivada que cai sob o expoente (neste caso, 2x^4 - x). A resposta para este problema então se torna 3(2x - x)(8x - 1).