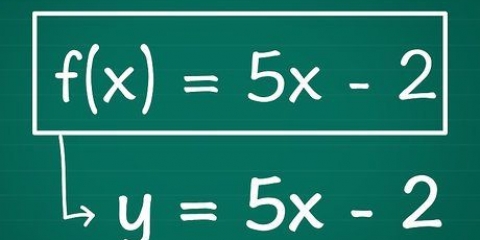Em seguida, processe -1 na função para obter a coordenada y. f(-1) = 3(-1) + 6(-1) -2 = 3 - 6 -2 = -5. O vértice da parábola é (-1,-5). Processe isso no gráfico desenhando um ponto na coordenada x -1 e na coordenada y -5. Isso deve estar no terceiro quadrante do gráfico. 
f(-2) = 3(-2) + 6(-2) -2 = -2. Um ponto no gráfico é (-2, -2) f(0) = 3(0) + 6(0) -2 = -2. Outro ponto no gráfico é (0,-2) f(1) = 3(1) + 6(1) -2 = 7. Um terceiro ponto no gráfico é (1, 7). 



Mas suponha que y = -3 é o ponto mais baixo do gráfico, mas aumenta para sempre. Então o intervalo é f(x) ≥ -3, e não mais do que isso. Suponha que o gráfico atinja seu ponto mais alto em y = 10, mas continue a cair para sempre. Então o intervalo é f(x) ≤ 10. 






Por exemplo: Se ela vender 2 ingressos você terá que multiplicar 2 por 5, com 10 como resposta, e assim o valor total arrecadado. 

Ou seja, qualquer número inteiro positivo que seja múltiplo de cinco é um resultado possível da função.
Determinando o escopo de uma função
Contente
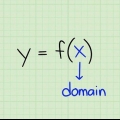
O intervalo de uma função é o conjunto de números que a função pode produzir. Em outras palavras, é o conjunto de valores de y que você obtém ao fatorar todos os valores de x possíveis na função. Este conjunto de valores x é chamado de domínio. Se você quiser saber como calcular o intervalo de uma função, siga os passos abaixo.
Degraus
Método 1 de 4: Determinando o intervalo de uma função com uma determinada equação

1. Escreva a equação. Suponha que você tenha a seguinte equação: f(x) = 3x + 6x -2. Isso significa que, quando você insere um valor para o X da equação, que você então tem um y-obtém valor. Esta é a função de uma parábola.

2. Encontre o vértice da função, se for uma equação quadrática. Se você tem uma linha reta ou qualquer função com um polinômio ou um número ímpar, como f(x) = 6x+2x + 7, você pode pular esta etapa. Mas se você estiver lidando com uma parábola ou uma equação onde a coordenada x é elevada ao quadrado ou aumentada por uma potência par, você terá que desenhar o vértice da parábola. Para isso, use a equação -b/2a para a coordenada x da função 3x + 6x -2, onde 3 = a, 6 = b e -2 = c. Nesse caso, -b é -6 e 2a é 6, então a coordenada x é -6/6, ou -1.

3. Encontre alguns outros pontos da função. Para ter uma ideia da função, você deve preencher alguns outros valores para x para ter uma ideia de como é a função antes de começar a procurar o intervalo. Como é uma parábola e x é positivo, a parábola apontará para cima (parábola do vale). Mas só para ter certeza, inserimos mais alguns valores para x para ver quais coordenadas y eles produzem:

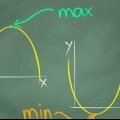
4. Encontre o intervalo do gráfico. Agora olhe para as coordenadas y no gráfico e encontre o ponto mais baixo onde o gráfico toca a coordenada y. Neste caso, a coordenada y mais baixa está no topo da parábola, -5 e o gráfico se estende infinitamente além deste ponto. Isso significa que o intervalo da função y = todos os números reais ≥ -5.
Método 2 de 4: Determinando o intervalo de uma função usando um gráfico

1. Encontre o mínimo da função. Encontre a menor coordenada y da função. Suponha que a função atinja seu ponto mais baixo em -3. Esta função pode ficar cada vez menor, até o infinito, então não tem ponto mais baixo fixo - apenas infinito.

2. Encontre o máximo da função. Suponha que a coordenada y mais alta da função seja 10. Esta função também pode se tornar infinitamente maior, então não tem ponto mais alto fixo - apenas infinito.

3. Indique qual é o intervalo. Isso significa que o intervalo da função, ou o intervalo das coordenadas y, é de -3 a 10. Então, -3 ≤ f(x) ≤ 10. Esse é o escopo da função.
Método 3 de 4: Determinando o escopo da função de um relacionamento

1. Anote o relacionamento. Uma relação é um conjunto de pares ordenados de coordenadas x e y. Você pode olhar para um relacionamento e determinar seu domínio e escopo. Suponha que você esteja lidando com a seguinte relação: {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}.

2. Liste as coordenadas y do relacionamento. Para determinar o intervalo da relação, anotamos todas as coordenadas y de cada par ordenado: {-3, 6, -1, 6, 3}.

3. Remova todas as coordenadas duplicadas para que você tenha apenas uma de cada coordenada y. Você deve ter notado que tem o "6" duas vezes na lista. Remova isso para que você fique com {-3, -1, 6, 3}.

4. Escreva o intervalo da relação em ordem crescente. Em seguida, organize os números no conjunto do menor para o maior e você encontrará o intervalo. O intervalo da relação {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} é {-3,-1, 3, 6}. Estás pronto.

5. Faça do relacionamento uma função é. Para uma relação ser uma função, toda vez que você insere um número de uma coordenada x, a coordenada y deve ser a mesma. Por exemplo, a relação {(2, 3) (2, 4) (6, 9)} é não função, porque se você preencher o 2 como x pela primeira vez, obterá um 3 como valor, mas na segunda vez que preencher um 2, obterá quatro. Uma relação é apenas uma função se você sempre obtiver a mesma saída para uma determinada entrada. Se você digitar -7, você deve sempre obter a mesma coordenada y (seja lá o que for), toda vez.
Método 4 de 4: Determine o escopo de uma função em um problema

1. Leia o problema. Suponha que você esteja trabalhando no seguinte problema: "Becky vende ingressos para o show de talentos de sua escola por US$ 5 cada. O valor total que ela arrecada é uma função do número de ingressos que ela vende. Qual é o alcance da função?"

2. Escreva o problema como uma função. Nesse caso m o valor arrecadado e t o número de ingressos vendidos. Como cada bilhete custa 5 euros, terá de multiplicar o número de bilhetes vendidos por 5 para obter o valor total. Portanto, a função pode ser escrita como M(t) = 5t.

3. Determine qual é o domínio. Para encontrar o intervalo, primeiro você precisa do domínio. O domínio consiste em todos os valores possíveis de t que participam da equação. Neste caso, Becky pode vender 0 ou mais ingressos – ela não pode vender um número negativo de ingressos. Como não sabemos o número de lugares no auditório da escola, podemos supor que, em teoria, ela pode vender um número infinito de ingressos. E ela só pode vender ingressos inteiros, não parte deles. Portanto, o domínio da função t = qualquer número inteiro positivo.

4. Determine qual é o intervalo. O intervalo é o valor possível que Becky pode levantar com a venda. Você terá que trabalhar com o domínio para encontrar o intervalo. Se você sabe que o domínio consiste em um inteiro positivo e que a equação M(t) = 5t então você também sabe que pode inserir qualquer número inteiro positivo nesta função para a resposta ou intervalo. Por exemplo: Se ela vender 5 ingressos, então M(5) = 5 x 5, ou 25 euros. Se ela vender 100, então M(100) = 5 x 100, ou 500 euros. Portanto, o intervalo da função qualquer número inteiro positivo que é um múltiplo de cinco.
Pontas
- Veja se você pode encontrar o inverso da função. O domínio da inversa de uma função é igual à imagem dessa função.
- Nos casos mais difíceis, pode ser mais fácil primeiro traçar o gráfico usando o domínio (se necessário) e depois ler o intervalo do gráfico.
- Verifique se a função se repete. Qualquer função que se repete ao longo do eixo x terá o mesmo intervalo para toda a função. Por exemplo: f(x) = sin(x) tem um intervalo entre -1 e 1.
Artigos sobre o tópico "Determinando o escopo de uma função"
Оцените, пожалуйста статью
Similar
Popular