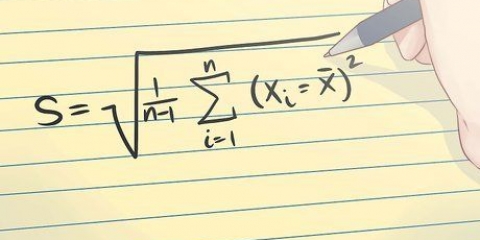Calculando a Soma dos Quadrados (sse)

Contente

Degraus

A soma dos quadrados, ou SSE, é um cálculo estatístico preliminar que leva a diferentes valores de dados. Quando você tem um conjunto de valores de dados, é útil poder determinar o quanto esses valores estão relacionados entre si. Você tem que organizar seus dados em uma tabela e depois fazer alguns cálculos bem simples. Depois de encontrar o SSE para um conjunto de dados, você pode encontrar a variância e o desvio padrão.

Degraus

Método 1 de 3: Calcule o SSE manualmente

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Passo 1

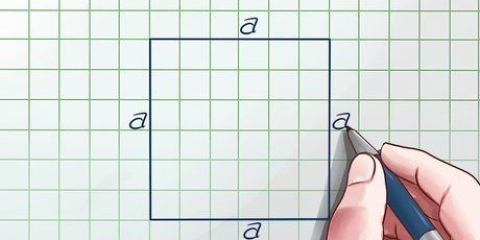
1. Faça uma tabela de três colunas. A maneira mais fácil de calcular o SSE é começar com uma tabela de três colunas. Rotule as três colunas

Onde o

${displaystyle {text{Valor}}}$ ,

desvio

${displaystyle {text{Desvio}}}$ , e

desvio 2

${displaystyle {text{Desvio}}^{2}}$ .

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Etapa 2

2. Preencha os detalhes. A primeira coluna contém os valores de suas medidas. Preencha a coluna

Onde o

${displaystyle {text{Valor}}}$ com suas leituras. Estes podem ser os resultados de um experimento, um estudo estatístico ou apenas dados de um problema de matemática.

Nesse caso, suponha que você esteja trabalhando com dados médicos e tenha uma lista das temperaturas corporais de dez pacientes. A temperatura corporal normal esperada é de 98,6 graus. A temperatura de dez pacientes é medida e dá os valores 99,0, 98,6, 98,5, 101,1, 98,3, 98,6, 97,9, 98,4, 99,2 e 99,1. A temperatura de dez pacientes é medida e dá os valores 99,0, 98,6, 98,5, 101,1, 98,3, 98,6, 97,9, 98,4, 99,2 e 99,1. Escreva esses valores na primeira coluna.

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Etapa 3

3. Calcule a média. Antes de calcular o erro para cada medição, você deve calcular a média de todo o conjunto de dados.

A média de um conjunto de dados é a soma de seus valores dividida pelo número de valores no conjunto. Isso pode ser representado simbolicamente, com a variável

μ

$mu$ :

μ = Σ X n

${displaystyle mu ={frac {Sigma x}{n}}}$

Para esses dados, a média é calculada da seguinte forma:

μ = 99, 0 + 98, 6 + 98, 5 + 101, 1 + 98, 3 + 98, 6 + 97, 9 + 98, 4 + 99, 2 + 99, 1 10

${displaystyle mu ={frac {99,0+98,6+98,5+101,1+98,3+98,6+97,9+98,4+99,2+99,1} {10}}}$

μ = 988, 7 10

${displaystyle mu ={frac {988.7}{10}}}$

μ = 98, 87

${estilo de exibição mu =98,87}$

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Etapa 4

4. Calcular os valores de erro individuais. Na segunda coluna da sua tabela você deve inserir os valores de erro para cada valor de dados. O erro é a diferença entre a leitura e a média.

Para o conjunto de dados fornecido, subtraia a média, 98,87, de cada valor medido e preencha a segunda coluna com os resultados. Esses dez cálculos são assim:

99, 0 - 98, 87 = 0, 13

${displaystyle 99,0-98,87=0,13}$

98, 6 - 98, 87 = - 0, 27

${displaystyle 98,6-98,87=-0,27}$

98, 5 - 98, 87 = - 0, 37

${displaystyle 98,5-98,87=-0,37}$

101, 1 - 98, 87 = 2, 23

${displaystyle 101,1-98,87=2,23}$

98, 3 - 98, 87 = - 0, 57

${displaystyle 98,3-98,87=-0,57}$

98, 6 - 98, 87 = - 0, 27

${displaystyle 98,6-98,87=-0,27}$

97, 9 - 98, 87 = - 0, 97

${estilo de exibição 97,9-98,87=-0,97}$

98, 4 - 98, 87 = - 0, 47

${displaystyle 98,4-98,87=-0,47}$

99, 2 - 98, 87 = 0, 33

${displaystyle 99,2-98,87=0,33}$

99, 1 - 98, 87 = 0, 23

${displaystyle 99,1-98,87=0,23}$

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Passo 5

5. Calcule o SSE. Na terceira coluna da tabela, encontre o quadrado de cada um dos valores resultantes na coluna do meio. Estes representam os quadrados do desvio da média para cada valor de dados medido.

Para cada valor na coluna do meio, use uma calculadora para calcular o quadrado. Registre os resultados na terceira coluna, como segue:

0, 13 2 = 0, 0169

${displaystyle 0,13^{2}=0,0169}$

(- 0, 27) 2 = 0, 0729

${displaystyle (-0,27)^{2}=0,0729}$

(- 0, 37) 2 = 0, 1369

${estilo de exibição (-0,37)^{2}=0,1369}$

2, 23 2 = 4, 9729

${displaystyle 2,23^{2}=4,9729}$

(- 0, 57) 2 = 0, 3249

${displaystyle (-0,57)^{2}=0,3249}$

(- 0, 27) 2 = 0, 0729

${displaystyle (-0,27)^{2}=0,0729}$

(- 0, 97) 2 = 0, 9409

${displaystyle (-0,97)^{2}=0,9409}$

(- 0, 47) 2 = 0, 2209

${displaystyle (-0,47)^{2}=0,2209}$

0, 33 2 = 0, 1089

${estilo de exibição 0,33^{2}=0,1089}$

0, 23 2 = 0, 0529

${displaystyle 0,23^{2}=0,0529}$

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Passo 6

6. Some os quadrados dos erros. O último passo é encontrar a soma dos valores na terceira coluna. O resultado desejado é o SSE, ou a soma dos quadrados dos erros.

Para este conjunto de dados, o SSE é calculado somando os dez valores na terceira coluna:

s s E = 6, 921

${displaystyle SSE=6.921}$

Método 2 de 3: Crie uma planilha do Excel para calcular o SSE

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Passo 7

1. Rotule as colunas da planilha. Você cria uma tabela com três colunas no Excel, com os mesmos três títulos acima.

Na célula A1, digite `Valor` como título.
Na caixa B1, digite `Desvio` como título.
Na caixa C1, digite `Desvio ao quadrado` como título.

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Passo 8

2. Insira seus dados. Na primeira coluna você deve inserir os valores de suas medidas. Se o conjunto for pequeno, você pode digitá-lo facilmente à mão. Se você tiver um grande conjunto de dados, talvez seja necessário copiar e colar os dados na coluna.

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Passo 9

3. Determine a média dos pontos de dados. O Excel tem uma função que calcula a média para você. Em uma célula vazia abaixo de sua tabela de dados (não importa qual célula você escolha), digite:

=Média(A2:___)

Não digite espaço vazio. Preencha esse espaço com o nome da célula do seu último ponto de dados. Por exemplo, se você tiver 100 pontos de dados, você usaria a função:

=Média(A2:A101)

Esta função contém os dados das células A2 a A101, pois a linha superior contém os títulos das colunas.

Quando você pressiona Enter ou clica em outra célula na tabela, a célula recém-programada é preenchida automaticamente com a média de seus valores de dados.

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Passo 10

4. Digite a função de medição de erro. Na primeira célula vazia na coluna `Desvio`, você deve inserir uma função para calcular a diferença entre cada ponto de dados e a média. Para fazer isso, use o nome da célula onde a média está localizada. Vamos supor que você esteja usando a célula A104 por enquanto.

A função de cálculo de erro, que você insere na célula B2, é:

=A2-$A$104. Os cifrões são necessários para garantir que você bloqueie a caixa A104 para cada cálculo.

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Passo 11

5. Preencha a função para os erros ao quadrado. Na terceira coluna você pode instruir o Excel para calcular o quadrado desejado.

Na célula C2, digite a seguinte função:

=B2^2

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Etapa 12

6. Copie as funções para preencher toda a tabela. Depois de inserir as funções na célula superior de cada coluna, B2 e C2, respectivamente, você precisa preencher toda a tabela. Você poderia redigitar a função em cada linha da tabela, mas isso levaria muito tempo. Usando o mouse, destaque as células B2 e C2 juntas e, sem soltar o botão do mouse, arraste para a célula inferior de cada coluna.

Supondo que você tenha 100 pontos de dados em sua tabela, arraste o mouse para as células B101 e C101.

Ao soltar o botão do mouse, as fórmulas são copiadas para todas as células da tabela. A tabela deve ser preenchida automaticamente com os valores calculados.

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Passo 13

7. Encontre o SSE. A coluna C da sua tabela contém todos os valores de erro ao quadrado. O último passo é deixar o Excel calcular a soma desses valores.

Em uma célula abaixo da tabela, provavelmente C102 neste exemplo, digite a seguinte função:

=Soma(C2:C101)

Clicar em Enter ou clicar em outra célula da tabela fornecerá o valor SSE de seus dados.

Método 3 de 3: Relacionando SSE a outros dados estatísticos

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Passo 14

1. Calcular o desvio do SSE. Encontrar o SSE para um conjunto de dados geralmente é um bloco de construção para encontrar outros valores mais úteis. A primeira delas é a variação. A variância é uma medida que indica o quanto os dados medidos se desviam da média. Na verdade, é a média das diferenças quadradas da média.

Como o SSE é a soma dos erros ao quadrado, você pode encontrar a média (essa é a variância) apenas dividindo pelo número de valores. No entanto, se você estiver calculando a variância de um conjunto de amostras, em vez de uma população inteira, estará dividindo a variância por (n-1) em vez de n. Assim:

Variação = SSE/n, se você calcular a variação de uma população inteira.
Variação = SSE/(n-1), se você calcular a variação de uma amostra de dados.

Para o problema amostral da temperatura dos pacientes, podemos supor que 10 pacientes compõem apenas uma amostra. Assim, a variância é calculada da seguinte forma:

Variação = SSE (n - 1)

${displaystyle {text{Variation}}={frac {text{SSE}}{(n-1)}}}$

Variação = 6, 921 9

${displaystyle {text{Variation}}={frac {6.921}{9}}}$

Variação = 0, 769

${displaystyle {text{Variation}}=0,769}$

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Passo 15

2. Calcular o desvio padrão do SSE. O desvio padrão é um valor comumente usado que indica o quanto os valores de um conjunto de dados se desviam da média. O desvio padrão é a raiz quadrada da variância. Observe que a variância é a média das medidas de erro ao quadrado.

Portanto, depois de calcular o SSE, você pode encontrar o desvio padrão da seguinte forma:

desvio padrão = \sqrt{SSE} n - 1

${displaystyle {text{Desvio Padrão}}={sqrt {frac {text{SSE}}{n-1}}}}$

Para a amostra das medições de temperatura, você pode encontrar o desvio padrão da seguinte forma:

desvio padrão = \sqrt{SSE} n - 1

${displaystyle {text{Desvio Padrão}}={sqrt {frac {text{SSE}}{n-1}}}}$

desvio padrão = \sqrt{\frac{6.921}{9}}

${displaystyle {text{Desvio Padrão}}={sqrt {frac {text{6.921}}{9}}}}$

desvio padrão = \sqrt{0, 769}

${displaystyle {text{Desvio Padrão}}={sqrt {0,769}}}$

desvio padrão = 0, 877

${displaystyle {text{Desvio padrão}}=0,877}$

Imagem intitulada Calcular a soma dos quadrados do erro (SSE) Passo 16

3. Use SSE para determinar a covariância. Este artigo se concentrou em conjuntos de dados que medem apenas um único valor por vez. No entanto, em muitos estudos você pode estar comparando dois valores separados. Por exemplo, você quer saber como esses dois valores se relacionam, não apenas com a média do conjunto de dados. Este valor é a covariância.

Os cálculos para covariância são muito detalhados para serem descritos aqui, exceto para observar que você usará o SSE para cada tipo de dados e depois o comparará. Para uma descrição mais detalhada da covariância e dos cálculos envolvidos, consulte encontre artigos sobre este tópico no wikiHow.

Como exemplo de uso de covariância, você pode comparar a idade dos pacientes em um estudo médico com a eficácia de um medicamento na redução da temperatura febril. Então você tem um conjunto de dados de idades e um segundo conjunto de dados de temperaturas. Você então encontra o SSE para cada conjunto de dados e, a partir daí, a variância, os desvios padrão e a covariância.