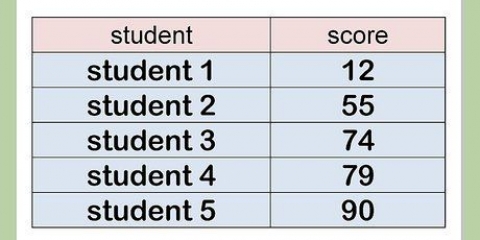
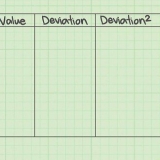
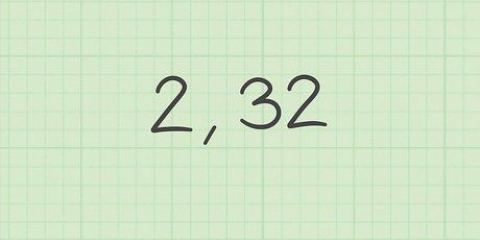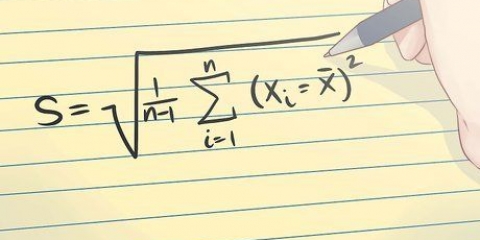No exemplo de coleta de dados, essas variações se tornam: 







Para verificar a validade de seus cálculos, verificamos se a soma dos valores na coluna de desvios é igual a zero. Se você somar todos os desvios e obtiver algo diferente de zero, sua média está incorreta ou você cometeu um erro no cálculo de um ou mais desvios. Devolva e confira seu trabalho. 
O valor absoluto é uma ferramenta matemática para indicar distância ou magnitude, independentemente da direção. Para determinar o valor absoluto, basta omitir o sinal de menos para cada número na segunda coluna. Então preencha a terceira coluna com os valores absolutos da seguinte forma: 









Para este conjunto de dados, o cálculo final será: 

Por exemplo, com este conjunto de dados, você pode dizer que a média é nove e a distância média da média é 2,75. Observe que alguns valores estão mais próximos de 2,75 em relação a outros. Mas 2,75 é a distância média.
Calculando o desvio médio da média
Ao trabalhar com dados, existem várias maneiras de medir com que precisão seus valores de dados são agrupados. O mais comum é a média. A maioria das pessoas aprende a calcular a média no início da escola encontrando a soma de um grupo de valores de dados e depois dividindo pelo número de valores no grupo. Um cálculo mais avançado é o desvio médio sobre a média. Este cálculo informa o quão perto seus valores estão da média. Você determina isso encontrando a média de um conjunto de dados, depois o desvio de cada dado dessa média e, em seguida, a média desses desvios.
Degraus
Parte 1 de 2: Calculando a média

1. Colete e conte seus dados. Para qualquer conjunto de valores, a média é uma medida do valor central. Dependendo do tipo de dados, a média fornecerá o valor médio desses dados. Para encontrar a média, primeiro você precisa coletar seus dados, seja por meio de um experimento ou apenas em uma tarefa.
- Como exemplo, usamos uma determinada sequência numérica 6, 7, 10, 12, 13, 4, 8 e 12. Essa sequência é pequena o suficiente para contar à mão e ver rapidamente que é uma sequência de oito números.
- Dentro da estatística, a variável
ou
frequentemente usado para indicar o número de valores em uma série ou coleção.

2. Encontre a soma dos valores. O primeiro passo para determinar a média é calcular a soma de todos os valores. Dentro da notação estatística, cada valor é geralmente representado pela variável  . A soma de todos os valores recebe o símbolo
. A soma de todos os valores recebe o símbolo  . A letra maiúscula grega sigma indica que é a soma dos valores. O cálculo para esta série simples é assim:
. A letra maiúscula grega sigma indica que é a soma dos valores. O cálculo para esta série simples é assim:
 . A soma de todos os valores recebe o símbolo
. A soma de todos os valores recebe o símbolo  . A letra maiúscula grega sigma indica que é a soma dos valores. O cálculo para esta série simples é assim:
. A letra maiúscula grega sigma indica que é a soma dos valores. O cálculo para esta série simples é assim:

3. Compartilhe para encontrar a média. Por fim, divida a soma pelo número de valores. A letra grega mu,  , é frequentemente usado para indicar a média. O cálculo da média, portanto, procede da seguinte forma:
, é frequentemente usado para indicar a média. O cálculo da média, portanto, procede da seguinte forma:
 , é frequentemente usado para indicar a média. O cálculo da média, portanto, procede da seguinte forma:
, é frequentemente usado para indicar a média. O cálculo da média, portanto, procede da seguinte forma:
Parte 2 de 2: Determinando o Desvio Médio

1. Criar uma tabela. Para manter seus dados em ordem e ajudar nos cálculos, é útil criar uma tabela de três colunas. Rotule a primeira coluna  . Rotule a segunda coluna
. Rotule a segunda coluna  . Rotule a terceira coluna
. Rotule a terceira coluna  .
.
 . Rotule a segunda coluna
. Rotule a segunda coluna  . Rotule a terceira coluna
. Rotule a terceira coluna  .
. - Preencha a primeira coluna com os valores para o seu cálculo.

2. Calcular o desvio (desvio) de cada valor. Na segunda coluna, rotulada  , coloque o desvio ou diferença entre cada valor e a média da série ou conjunto. Encontre esse valor subtraindo a média de cada valor de dados.
, coloque o desvio ou diferença entre cada valor e a média da série ou conjunto. Encontre esse valor subtraindo a média de cada valor de dados.
 , coloque o desvio ou diferença entre cada valor e a média da série ou conjunto. Encontre esse valor subtraindo a média de cada valor de dados.
, coloque o desvio ou diferença entre cada valor e a média da série ou conjunto. Encontre esse valor subtraindo a média de cada valor de dados.








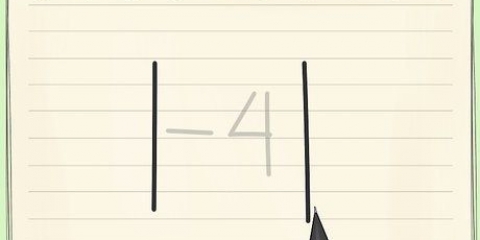
3. Determine o valor absoluto de cada desvio. Quando você calcula o desvio de qualquer valor da média, você só quer saber a diferença, não se essa diferença é positiva ou negativa. O que você realmente precisa, em termos matemáticos, é o valor absoluto da diferença. O valor absoluto é indicado por barras verticais| |.










4. Calcular a média dos desvios absolutos. Depois de completar a tabela de três colunas, encontre a média dos valores absolutos na terceira coluna. Assim como você fez para calcular a média dos valores iniciais, some os desvios e divida a soma pelo número de valores.


5. Interprete o resultado. O valor do desvio médio da média é uma medida de quão próximos os valores estão um do outro. Isso responde à pergunta: "Quão próximos da média estão os valores dos dados?"?`
Pontas
- Continue praticando e você será capaz de calculá-lo sem problemas.
Artigos sobre o tópico "Calculando o desvio médio da média"
Оцените, пожалуйста статью
Popular