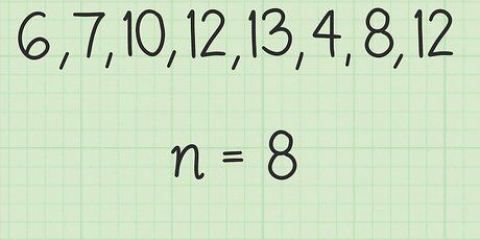Calculando o erro padrão

1. O desvio padrão. O desvio padrão de uma amostra indica o grau de dispersão dos números. O desvio padrão de uma amostra é geralmente denotado por um s. A fórmula matemática para o desvio padrão é mostrada acima.

2. A média da população. A média populacional é a média de um conjunto de dados numéricos que contém todos os valores de todo o grupo — em outras palavras, a média de um conjunto completo de números, em vez de uma amostra.

3. A média aritmética. Esta é apenas uma média: a soma de um número de valores, dividida por esse mesmo número de valores.

4. Reconhecer meios de amostra. Quando uma média aritmética é baseada em uma série de observações obtidas por amostragem de uma população estatística, ela é chamada de “média amostral”.” Esta é a média de um conjunto numérico de dados em que alguns dos valores dentro de um grupo estão contidos. É referido como:

5. A distribuição normal. A distribuição normal, a mais comumente usada de todas as distribuições, é simétrica, com um outlier na média dos dados. A forma do gráfico é a de um relógio, com a inclinação sendo igual em ambos os lados do topo. Cinquenta por cento da distribuição está à esquerda e cinquenta por cento à direita. A distribuição de uma distribuição normal é determinada pelo desvio padrão.

6. A fórmula padrão. A fórmula para o erro padrão de uma média amostral é dada acima.

1. Calcular a média amostral. Para determinar o erro padrão, primeiro você precisará calcular o desvio padrão (porque o desvio padrão, s, é parte da fórmula do erro padrão). Comece calculando a média dos valores da amostra. A média da amostra é expressa como a média aritmética das medições x1, x2, . . . xn. Isso é calculado com a fórmula acima.

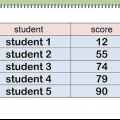
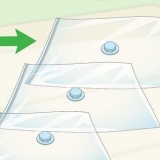
• Por exemplo, suponha que você precise calcular o erro padrão de uma média amostral para as medidas do peso de cinco moedas, conforme listado na tabela abaixo:
  Você então calcularia a média da amostra inserindo os valores de peso na fórmula, assim:

2. Subtraia a média da amostra de cada medição e eleve este valor ao quadrado. Depois de obter a média da amostra, você pode expandir a tabela subtraindo-a de cada medição individual e, em seguida, elevando o resultado ao quadrado.

3. Determine o desvio total de suas leituras da média da amostra. O desvio total é a média da diferença quadrada da média da amostra. Adicione todos os valores juntos para determinar isso.

4. Calcule o desvio quadrado médio das medições da média da amostra. Depois de conhecer o desvio total, você pode encontrar o desvio médio usando n -1. Observe que n é igual ao número de medidas.

5. Determine o desvio padrão. Agora você tem todos os valores necessários para usar a fórmula do(s) desvio(s) padrão.

1. Use o desvio padrão para calcular o erro padrão com a fórmula padrão.

• No exemplo acima, você calcula o erro padrão da seguinte forma:
  Portanto, o erro padrão (o desvio padrão da média da amostra) é 0,0032031 gramas.

Pontas

• O erro padrão e o desvio padrão são frequentemente confundidos. Observe que o erro padrão é uma descrição do desvio padrão da distribuição amostral de um valor estatístico, não a distribuição dos valores individuais.
• Em revistas científicas, o erro padrão e o desvio padrão às vezes são usados ​​​​de forma intercambiável. Um sinal ± é usado para unir as duas leituras.