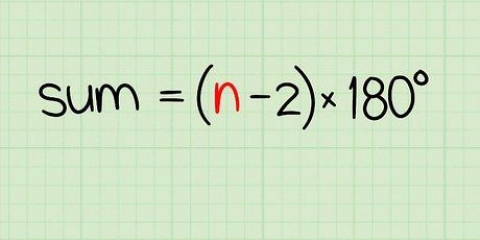Por exemplo, se você deseja calcular a soma das séries 10, 15, 20, 25, 30, então  , porque há cinco números na sequência.
, porque há cinco números na sequência. 
Por exemplo, na sequência 10, 15, 20, 25, 30  , e
, e  .
. 

Por exemplo, se houver cinco números em sua sequência, onde 10 é o primeiro número e 30 é o último número, sua fórmula ficará assim:  .
. 
Por exemplo:



Por exemplo:


Então a soma da série (10, 15, 20, 25, 30) é igual a 100. 

Determine o número de números ( ) nas séries. Como você começa com três, termina com 24 e adiciona sete a cada vez, a sequência de números é 3, 10, 17, 24. (O fator de diferença é a diferença entre cada número na série.) Isso significa que
) nas séries. Como você começa com três, termina com 24 e adiciona sete a cada vez, a sequência de números é 3, 10, 17, 24. (O fator de diferença é a diferença entre cada número na série.) Isso significa que 
Determine o primeiro ( ) e por ultimo (
) e por ultimo ( ) número na sequência. Como a sequência é de 3 a 24,
) número na sequência. Como a sequência é de 3 a 24,  e
e  .
. Encontre a média de  e
e  :
:  .
. Multiplique a média por  :
:  .
. 
Determine o número de termos ( ) nas séries. Porque Mara economiza por 52 semanas, (1 ano),
) nas séries. Porque Mara economiza por 52 semanas, (1 ano),  .
. Determine o primeiro ( ) e por ultimo (
) e por ultimo ( ) número na sequência. A primeira quantia que ela economiza é de cinco euros, então
) número na sequência. A primeira quantia que ela economiza é de cinco euros, então  . Para calcular o valor total economizado na última semana do ano, calculamos
. Para calcular o valor total economizado na última semana do ano, calculamos  . assim
. assim  .
. Determina a média de  e
e  :
:  .
. Multiplique a média por  :
:  . Então ela economizou € 6.890 no final do ano.
. Então ela economizou € 6.890 no final do ano.
Encontrar a soma de uma sequência aritmética
Contente
Uma sequência aritmética é uma sequência de números em que cada número aumenta de um valor constante. Para a soma de uma sequência aritmética, você pode somar todos os números. No entanto, isso não é realmente prático quando a sequência contém um grande número de termos. Em vez disso, você pode encontrar rapidamente a soma de cada sequência aritmética multiplicando a média do primeiro e do último número pelo número de termos na sequência.
Degraus
Parte 1 de 3: Analisando sua sequência

1. Certifique-se de ter uma sequência aritmética. Uma sequência aritmética é uma lista ordenada de números, onde a mudança dos números é constante. Este método só funciona se o seu conjunto de números for uma sequência aritmética.
- Para determinar se você está lidando com uma sequência aritmética, encontre a diferença entre o primeiro ou o último par de números. Certifique-se de que a diferença é sempre a mesma.
- Por exemplo, a sequência dos números 10, 15, 20, 25, 30 é uma sequência aritmética, porque a diferença entre cada número é constantemente cinco.

2. Determine o número de termos em sua sequência. Todo número é um termo. Se apenas um número for mencionado, você pode contá-los. Se você conhece o primeiro número, o último número e o fator de diferença (a diferença entre cada número), você pode usar uma fórmula para determinar o número de números. Este número é apresentado pela variável  .
.
 .
. , porque há cinco números na sequência.
, porque há cinco números na sequência.
3. Encontre o primeiro e o último número na sequência. Você precisa conhecer os dois números para calcular a soma da sequência aritmética. Muitas vezes o primeiro número será um, mas nem sempre. Defina a variável  igual ao primeiro número da sequência, e
igual ao primeiro número da sequência, e  igual ao último número da sequência.
igual ao último número da sequência.
 igual ao primeiro número da sequência, e
igual ao primeiro número da sequência, e  igual ao último número da sequência.
igual ao último número da sequência. , e
, e  .
.Parte 2 de 3: Calcule a soma

1. Escreva a fórmula para encontrar a soma de uma sequência aritmética. A fórmula é  , através do qual
, através do qual  é igual à soma da série.
é igual à soma da série.
 , através do qual
, através do qual  é igual à soma da série.
é igual à soma da série. - Observe que esta fórmula indica que a soma da sequência aritmética é igual à média do primeiro e do último número multiplicado pelo número de números.

2. Insira os valores n  ,
, uma 1  e
e uma n  na fórmula em. Certifique-se de substituir corretamente.
na fórmula em. Certifique-se de substituir corretamente.
 ,
,  e
e  na fórmula em. Certifique-se de substituir corretamente.
na fórmula em. Certifique-se de substituir corretamente. .
.
3. Calcule a média do primeiro e do segundo número. Você faz isso somando os dois números e dividindo por dois.



4. Multiplique a média pelo número de números na série. Isto dá-lhe a soma da sequência aritmética.


Então a soma da série (10, 15, 20, 25, 30) é igual a 100.
Parte 3 de 3: Completando os problemas de amostra

1. Encontre a soma dos números de 1 a 500. Incluir todos os números inteiros consecutivos no cálculo.
- Determine o número de termos (
) nas séries. Como você está contando todos os números inteiros consecutivos até 500, inclusive,
.
- Determine o primeiro (
) e por ultimo (
) número na sequência. Como assumimos a série de 1 a 500, é válido que
e
.
- Encontre a média de
e
:
.
- Multiplique a média por
:
.

2. Encontre a soma da sequência aritmética indicada. O primeiro número da sequência é três. O último número da sequência é 24. O fator de diferença é sete.
 ) nas séries. Como você começa com três, termina com 24 e adiciona sete a cada vez, a sequência de números é 3, 10, 17, 24. (O fator de diferença é a diferença entre cada número na série.) Isso significa que
) nas séries. Como você começa com três, termina com 24 e adiciona sete a cada vez, a sequência de números é 3, 10, 17, 24. (O fator de diferença é a diferença entre cada número na série.) Isso significa que 
 ) e por ultimo (
) e por ultimo ( ) número na sequência. Como a sequência é de 3 a 24,
) número na sequência. Como a sequência é de 3 a 24,  e
e  .
. e
e  :
:  .
. :
:  .
.
3. Resolva o seguinte problema. Mara poupa 5 euros na primeira semana do ano. Durante o resto do ano, ela aumenta suas economias em 5 euros todas as semanas. Quanto dinheiro Mara economizou no final do ano?
 ) nas séries. Porque Mara economiza por 52 semanas, (1 ano),
) nas séries. Porque Mara economiza por 52 semanas, (1 ano),  .
. ) e por ultimo (
) e por ultimo ( ) número na sequência. A primeira quantia que ela economiza é de cinco euros, então
) número na sequência. A primeira quantia que ela economiza é de cinco euros, então  . Para calcular o valor total economizado na última semana do ano, calculamos
. Para calcular o valor total economizado na última semana do ano, calculamos  . assim
. assim  .
. e
e  :
:  .
. :
:  . Então ela economizou € 6.890 no final do ano.
. Então ela economizou € 6.890 no final do ano.Artigos sobre o tópico "Encontrar a soma de uma sequência aritmética"
Оцените, пожалуйста статью
Similar
Popular