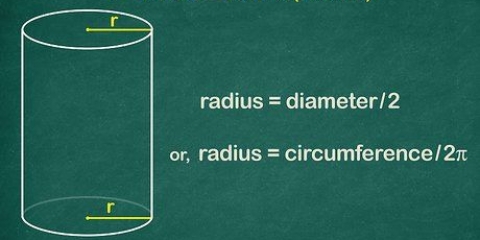
Se você está tentando resolver uma soma de histórias, o raio já pode ser fornecido. Talvez a soma já indique qual é o diâmetro, ou a distância entre um lado do círculo e o outro lado do círculo, passando pelo centro. O raio é exatamente a metade do diâmetro. Você pode medir o raio com uma régua se quiser calcular a área de um cilindro real. 
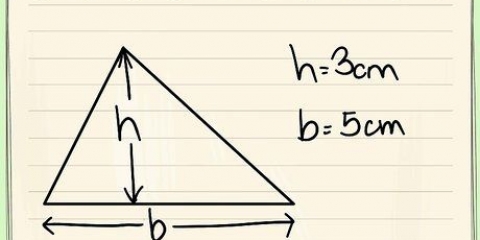
Para calcular a área do círculo superior, basta inserir o raio (3 centímetros) na equação para calcular a área de um círculo. A = r. É assim que você faz isso: A = r A = π x 3 A = π x 9 = 28,26 cm 






Calcular a área de um cilindro
Contente
A área de um cilindro é a soma das áreas das paredes superior, inferior e laterais. Para calcular a área de um cilindro, você precisa calcular a área da parte superior e inferior circular e adicionar esse número à área da parede lateral. A fórmula para calcular a área de um cilindro é A = 2πr + 2πrh.
Degraus
Parte 1 de 3: Calculando a área dos círculos (2 x (π x r))

1. Imagine a parte superior e inferior de um cilindro. Uma lata de sopa tem a forma de um cilindro. Se você pensar bem, verá que a lata tem um topo e um fundo iguais. Tanto a parte superior quanto a inferior têm a forma de um círculo. O primeiro passo para calcular a área do cilindro é calcular a área de ambas as extremidades circulares.

2. Encontre o raio do cilindro. O raio, ou raio, é a distância entre o centro de um círculo e a borda externa desse círculo. O raio é indicado pela letra "r". O raio do seu cilindro é o mesmo que o raio da parte superior e inferior circular. Neste exemplo, o raio da base é de 3 centímetros.

3. Calcule a área do círculo superior. A área de um círculo é igual ao número pi (~3,14) multiplicado pelo raio do círculo ao quadrado. A equação é escrita como π x r. Isso é o mesmo que π x r x r.

4. Faça o mesmo para o círculo do outro lado. Agora que você calculou a área de um dos círculos, você também deve calcular a área do outro círculo. Você pode seguir as mesmas etapas do primeiro círculo ou pode ver que ambos os círculos são idênticos. Se você entender isso, não precisará fazer o cálculo novamente para o segundo círculo.
Parte 2 de 3: Calculando a área da parede lateral (2π x r x h)

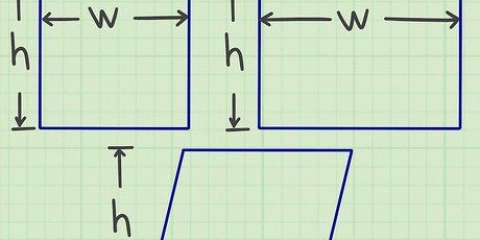
1. Imagine a parede lateral de um cilindro. Quando você imagina uma lata de sopa cilíndrica, deve ver uma base na parte superior e inferior. Essas superfícies são conectadas entre si por uma parede lateral feita de estanho. O raio da parede lateral é igual ao raio das bases, mas a parede lateral tem uma altura e as bases não.

2. Encontre a circunferência de um dos círculos. Você precisará calcular esse perímetro para encontrar a área da parede lateral (também conhecida como área lateral). Para calcular a circunferência, basta multiplicar o raio por 2π. Então você pode calcular a área multiplicando 3 centímetros por 2π. 3 centímetros x 2π = 18,84 centímetros.

3. Multiplique a circunferência do círculo pela altura do cilindro. Você então obtém a área da parede lateral. Multiplique a circunferência (18,84 centímetros) pela altura (5 centímetros). 18,84 centímetros x 5 centímetros = 94,2 centímetros.
Parte 3 de 3: Calculando a área completa ((2) x (π x r)) + (2π x r x h)

1. Imagine o cilindro completo. Primeiro você imaginou como seria o topo e o fundo circulares e calculou a área de ambos os círculos. Então você pensou na parede lateral que conecta os dois círculos e calculou a área dela. Agora você está tentando imaginar a lata inteira porque agora você vai calcular a área do cilindro inteiro.

2. Calcule a área de ambos os círculos juntos. Basta multiplicar o resultado anterior (28,26 cm) por 2 para calcular a área dos dois círculos juntos. 28,26 x 2 = 56,52 cm. Esta é a área de ambos os círculos.

3. Adicione a área da parede lateral e a área de ambos os círculos juntos. Quando você adicionou a área de ambos os círculos à área da parede lateral, calculou a área de todo o cilindro. Você só precisa adicionar 56,52 cm (a área dos dois círculos juntos) e 94,2 cm (a área da parede lateral). 56,52 cm + 94,2 cm = 150,72 cm. Portanto, a área de um cilindro com uma altura de 5 centímetros e uma base circular com um raio de 3 centímetros é 150,72 cm.
Pontas
- Se houver uma raiz quadrada em altura ou raio, descubra como multiplicar, subtrair e adicionar raízes quadradas para saber mais sobre isso. Você também pode perguntar ao seu professor.
Avisos
- Lembre-se de sempre multiplicar a área da base circular por 2 para incluir também a área do segundo círculo.
Artigos sobre o tópico "Calcular a área de um cilindro"
Оцените, пожалуйста статью
Popular