Por exemplo, se o último número for 81, você calcula 81 + 1 = 82. 
Por exemplo: 82 / 2 = 41. 
Por exemplo: 41 x 41 = 1681. Isso significa que a soma de todos os números ímpares consecutivos entre 1 e 81 é igual a 1681. 

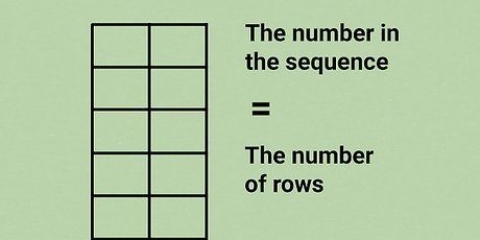
Soma do primeiro número ímpar = 1. A raiz quadrada de 1 é 1, e apenas um dígito foi adicionado. Soma dos dois primeiros números ímpares = 1 + 3 = 4. A raiz quadrada de 4 é 2, e dois números foram adicionados. Soma dos três primeiros números ímpares = 1 + 3 + 5 = 9. A raiz quadrada de 9 é 3, e três dígitos são adicionados. Soma dos quatro primeiros números ímpares = 1 + 3 + 5 + 7 = 16. A raiz quadrada de 16 é 4, e quatro dígitos são somados. 
Por exemplo, se você inserir 41 para n, então você tem 41 x 41, ou 1681, que é igual à soma dos primeiros 41 números ímpares. Se você não sabe com quantos números está lidando, a fórmula é obter a soma entre 1 e n a ser determinado: (1/2(n + 1)) 


Isso significa que o segundo número na sequência n + torna-se 2, o terceiro número`n` + 4, etc. 
Por exemplo, se você for solicitado a determinar uma sequência de dois números ímpares consecutivos que somam 128, você escreveria n + n + 2 = 128. 
Por exemplo: n + n + 2 = 128 é simplificado para 2n + 2 = 128. 
Faça a adição e a subtração primeiro. Nesse caso, você precisa subtrair dois de ambos os lados da equação para obter n para obtê-lo por conta própria, então 2n = 126. Em seguida, realizamos a multiplicação e a divisão. Neste caso, você precisa dividir ambos os lados por dois, para n isolar, assim n = 63. 
A resposta para este problema é 63 e 65, porque n = 63 e n + 2 = 65. É sempre uma boa ideia verificar seu trabalho colocando seus números de volta na equação. Se eles não forem iguais à soma fornecida, tente novamente desde o início.
Adicionar uma sequência de números ímpares consecutivos juntos
Contente
Você pode adicionar manualmente uma série de números ímpares consecutivos, mas há uma maneira muito mais fácil de fazer isso, especialmente se for muitos números. Depois de dominar uma fórmula simples, você pode somar esses números rapidamente, sem usar uma calculadora. Há também uma maneira fácil de descobrir quais números consecutivos somam uma determinada soma.
Degraus
Parte 1 de 3: A fórmula para adicionar uma série de números ímpares consecutivos

1. Escolha um ponto final. Antes de começar, determine qual será o último número consecutivo em sua sequência. Esta fórmula pode ajudá-lo a adicionar qualquer número de números ímpares consecutivos começando com 1.
- Se você tiver que fazer um problema, este número será dado. Por exemplo, se lhe perguntarem qual é a soma de todos os números ímpares consecutivos entre 1 e 81, seu ponto final é 81.

2. Adicione 1 a ele. O próximo passo é simplesmente adicionar 1 ao último número. Agora você deve ter um número par, o que é essencial para a próxima etapa.

3. Dividir por dois. Depois de obter um número par, você deve dividi-lo por dois. Isso lhe dará um número ímpar igual ao número de dígitos somados.

4. Quadrar a soma. O último passo é elevar o número ao quadrado (multiplicar um número por ele mesmo). Se você fizer isso, você terá sua resposta.
Parte 2 de 3: Entendendo por que a fórmula funciona

1. Observe o padrão. A chave para entender esta fórmula é reconhecer o padrão subjacente. A soma de uma série de números ímpares consecutivos começando com um é sempre igual ao quadrado do número de dígitos somados.
- Soma do primeiro número ímpar = 1
- Soma dos dois primeiros números ímpares = 1 + 3 = 4 (= 2 x 2).
- Soma dos três primeiros números ímpares = 1 + 3 + 5 = 9 (= 3 x 3).
- Soma dos quatro primeiros números ímpares = 1 + 3 + 5 + 7 = 16 (= 4 x 4).

2. Entenda os dados intermediários. Ao resolver este problema, você sabe mais do que apenas a soma dos números. Você também sabe quantos números consecutivos são somados: 41! Isso ocorre porque o número de dígitos adicionados sempre é igual à raiz quadrada da soma.

3. Faça a fórmula geral. Depois de entender a fórmula e como ela funciona, você pode anotá-la em um formato apropriado, independentemente dos números com os quais está lidando. A fórmula para obter a soma do primeiro n números ímpares podem ser encontrados n x n ou n ao quadrado.
Parte 3 de 3: Determinando quais números ímpares consecutivos somam uma determinada soma

1. Entenda a diferença entre os dois tipos de problemas. Se você receber uma série de números ímpares consecutivos e for solicitado a encontrar sua soma, você deve usar a equação (1/2(n + 1)) usar. Se, por outro lado, você recebeu uma soma e foi solicitado a encontrar a sequência de números ímpares consecutivos que leva a essa soma, então você deve usar uma fórmula completamente diferente.

2. Sair n ser igual ao primeiro número. Para descobrir quais números ímpares consecutivos dão uma determinada soma, você precisa fazer uma fórmula algébrica. Começar com n para exibir o primeiro número na sequência.

3. Escreva os números restantes em termos den. Você precisa determinar como obter o resto dos números na sequência em termos de n escreve. Como todos são números ímpares consecutivos, haverá uma diferença de dois entre cada número.

4. Arredonde sua fórmula. Depois de saber como representar cada número na sequência, é hora de escrever sua fórmula. O lado esquerdo da sua fórmula deve representar os números na sequência e o lado direito a soma.

5. Simplifique a equação. Se você tiver mais de um n à esquerda da sua equação, some-os. Isso facilita muito a resolução.

6. isolarn. O último passo para resolver esta equação é n sozinho em um lado da equação. Lembre-se de que quaisquer alterações que você fizer em um lado da equação, você também terá que fazê-las no outro lado.

7. Escreva sua resposta. Neste momento você sabe que n = 63, mas você ainda não está pronto. Você tem que certificar-se de responder à pergunta feita completamente. Se a pergunta perguntar qual sequência de números ímpares consecutivos leva a uma certa soma, você deve escrever todos os números.
Artigos sobre o tópico "Adicionar uma sequência de números ímpares consecutivos juntos"
Оцените, пожалуйста статью
Similar
Popular