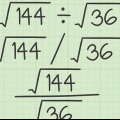Exemplo 1: Resolva:  .
.
Comece convertendo isso em um logaritmo usando a fórmula acima: .
. Esta fórmula é a fórmula de `mudança de base`, derivada das propriedades logarítmicas básicas. 
Exemplo 1 (cont.): Reescrever  E se
E se  . O valor de `?` é a resposta para o problema. Você pode ter que tentar alguns para encontrá-lo:
. O valor de `?` é a resposta para o problema. Você pode ter que tentar alguns para encontrá-lo:



16 é o que você estava procurando, então = 4.
= 4. 
Exemplo 2: O que é  ?
? Converta isso para um logaritmo::  .(Observe que o 3 desaparece em qualquer log inicial -- isso se aplica a qualquer base).
.(Observe que o 3 desaparece em qualquer log inicial -- isso se aplica a qualquer base). Reescrever como  e testar possíveis valores de ?:
e testar possíveis valores de ?:


Como 58 está entre esses dois números, nenhum inteiro como resposta.
nenhum inteiro como resposta. Deixe sua resposta como:  .
. 

Se tanto x ou y é negativo, não há solução para o problema. E se Ambas x se y for negativo, remova os sinais negativos usando a propriedade 
Não há logaritmos de números negativos no problema de exemplo, então você pode prosseguir para a próxima etapa. 
Use isso para expandir o lado esquerdo do problema de amostra:

Substituindo isso de volta na equação original:

→


O problema de exemplo tem um novo termo:  . Como 3 = 27, simplifique
. Como 3 = 27, simplifique  nojento 3.
nojento 3. A comparação completa agora é:




 .
.
No problema de exemplo, o n ainda preso no termo  .
.
Em volta do n para isolar, use a regra do produto dos logaritmos:

Substituindo isso de volta na equação completa:





Desde 3 = 19683, n = 19683
Compartilhando logaritmos
Contente
Logaritmos podem parecer difíceis de usar, mas assim como expoentes ou polinômios, você só precisa aprender as técnicas certas. Você só precisa conhecer algumas propriedades básicas para dividir dois logaritmos com a mesma base ou estender um logaritmo por um quociente.
Degraus
Método 1 de 2: Dividindo logaritmos manualmente

1. Verifique se há números negativos e uns. Este método lida com problemas na forma  . No entanto, isso não funciona para alguns casos especiais:
. No entanto, isso não funciona para alguns casos especiais:
 . No entanto, isso não funciona para alguns casos especiais:
. No entanto, isso não funciona para alguns casos especiais: - O logaritmo de um número negativo não é definido para todas as bases (como
ou
). Em seguida, escreva `Sem solução`.
- O logaritmo de zero também é indefinido para todas as bases. Se você vir um termo como
, em seguida, escreva também `Sem solução`.
- O logaritmo de um em qualquer base (
) é sempre igual a zero, pois
para todos os valores de X. Substitua esse logaritmo por 1 em vez de usar o método abaixo.
- Se os dois logaritmos tiverem bases diferentes, como
, e você não pode simplificar nenhum deles para um número inteiro, então o problema não pode ser resolvido manualmente.

2. Edite a expressão em um logaritmo. Supondo que você não encontrou nenhuma das exceções acima, agora você pode simplificar o problema em um logaritmo. Para isso, use a fórmula .
.
 .
. .
.Comece convertendo isso em um logaritmo usando a fórmula acima:
 .
.
3. Calcule isso manualmente, se possível. Lembre-se: oh  para resolver, você pensa em `
para resolver, você pensa em ` ` ou `Qual expoente posso usar uma elevar para X para obter?` Nem sempre é possível resolver isso sem uma calculadora, mas se você tiver sorte, acabará com um logaritmo facilmente simplificado.
` ou `Qual expoente posso usar uma elevar para X para obter?` Nem sempre é possível resolver isso sem uma calculadora, mas se você tiver sorte, acabará com um logaritmo facilmente simplificado.
 para resolver, você pensa em `
para resolver, você pensa em ` ` ou `Qual expoente posso usar uma elevar para X para obter?` Nem sempre é possível resolver isso sem uma calculadora, mas se você tiver sorte, acabará com um logaritmo facilmente simplificado.
` ou `Qual expoente posso usar uma elevar para X para obter?` Nem sempre é possível resolver isso sem uma calculadora, mas se você tiver sorte, acabará com um logaritmo facilmente simplificado. E se
E se  . O valor de `?` é a resposta para o problema. Você pode ter que tentar alguns para encontrá-lo:
. O valor de `?` é a resposta para o problema. Você pode ter que tentar alguns para encontrá-lo:


16 é o que você estava procurando, então
 = 4.
= 4.
4. Deixe a resposta em forma de logaritmo se você não puder simplificá-la. Alguns logaritmos são muito difíceis de resolver manualmente. Você precisa de uma calculadora se precisar da resposta para um propósito prático. Quando você resolve problemas na aula de matemática, seu professor provavelmente espera que você deixe a resposta como logaritmo. Aqui está outro exemplo que usa esse método para um problema mais complicado:
 ?
? .(Observe que o 3 desaparece em qualquer log inicial -- isso se aplica a qualquer base).
.(Observe que o 3 desaparece em qualquer log inicial -- isso se aplica a qualquer base). e testar possíveis valores de ?:
e testar possíveis valores de ?:

Como 58 está entre esses dois números,
 nenhum inteiro como resposta.
nenhum inteiro como resposta. .
.Método 2 de 2: Trabalhando com o logaritmo de um quociente

1. Comece com um problema de divisão em um logaritmo. Esta seção ajuda você a resolver problemas com expressões na forma  .
.
 .
. - Por exemplo, comece com este problema:
`Resolva para n se.`

2. Verifique se há números negativos. O logaritmo de um número negativo é indefinido. Se x ou y forem um número negativo, verifique se o problema tem solução antes de continuar:


3. Divida o quociente em dois logaritmos. Uma propriedade útil dos logaritmos é descrita pela fórmula:  . Em outras palavras, o logaritmo de um quociente é sempre igual ao logaritmo do numerador, menos o logaritmo do denominador.
. Em outras palavras, o logaritmo de um quociente é sempre igual ao logaritmo do numerador, menos o logaritmo do denominador.
 . Em outras palavras, o logaritmo de um quociente é sempre igual ao logaritmo do numerador, menos o logaritmo do denominador.
. Em outras palavras, o logaritmo de um quociente é sempre igual ao logaritmo do numerador, menos o logaritmo do denominador.

→


4. Simplifique os logaritmos se possível. Se algum dos novos logaritmos na expressão for um número inteiro, simplifique-os agora.
 . Como 3 = 27, simplifique
. Como 3 = 27, simplifique  nojento 3.
nojento 3.

5. Isolar a variável. Como qualquer problema de matemática, ajuda a isolar o termo com a variável em um lado da equação. Elimine termos semelhantes sempre que possível para simplificar a equação.


 .
.
6. Use propriedades adicionais de logaritmos quando necessário. Para isolar a variável de outros termos dentro do mesmo logaritmo, reescreva o termo usando diferentes propriedades logarítmicas.
 .
.Em volta do n para isolar, use a regra do produto dos logaritmos:





7. Continue simplificando até encontrar a solução. Repita as mesmas técnicas algébricas e logarítmicas para resolver o problema. Se não houver solução inteira, use uma calculadora e arredondar para o número significativo mais próximo.


Desde 3 = 19683, n = 19683
Artigos sobre o tópico "Compartilhando logaritmos"
Оцените, пожалуйста статью
Popular