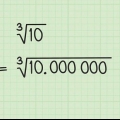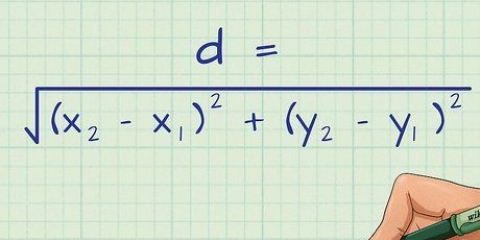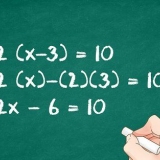Calculando a Sequência de Fibonacci (com Imagens)

Contente

Degraus
- Método 1 de 2: use uma tabela
- Método 2 de 2: Usando a fórmula de Binet e a Média Dourada

A sequência de Fibonacci é uma sequência de números gerada pela adição dos dois números anteriores na sequência. Os números da série são frequentemente vistos na natureza e na arte, como espirais e a proporção áurea. A maneira mais fácil de calcular a série é preparar uma tabela; no entanto, isso não é prático se você estiver procurando o 100º termo na sequência, por exemplo, nesse caso você usará a fórmula de Binet.

Degraus

Método 1 de 2: use uma tabela

Imagem intitulada Calcule a sequência de Fibonacci Passo 1

1. Criar uma tabela com duas colunas. O número de linhas depende do número de números na sequência de Fibonacci que você deseja calcular.

Por exemplo, se você quiser encontrar o quinto número na sequência, sua tabela terá cinco linhas.
Com este método de tabela não é possível encontrar nenhum número mais abaixo na sequência sem primeiro calcular todos os números anteriores. Por exemplo, se você quiser encontrar o 100º número na sequência, primeiro precisará encontrar os primeiros 99 números. Portanto, o método da tabela só funciona para números no início da sequência.

Imagem intitulada Calcule a sequência de Fibonacci Etapa 2

2. Digite a sequência de números na coluna da esquerda. Isso significa preencher uma sequência de números ordinais consecutivos, começando com "1º."

O termo refere-se à posição do número na sequência de Fibonacci.

Por exemplo, se você quiser calcular o quinto número na sequência, escreva 1º, 2º, 3º, 4º, 5º na coluna da esquerda. Isso irá ajudá-lo a identificar os primeiros cinco termos da sequência.

Imagem intitulada Calcule a sequência de Fibonacci Passo 3

3. Coloque 1 na primeira linha da coluna da direita. Este é o ponto de partida da sequência de Fibonacci. Em outras palavras, o primeiro termo da sequência é 1.

A sequência correta de Fibonacci sempre começa com 1. Se você quiser começar com um número diferente, não encontrará o padrão correto da sequência de Fibonacci.

Imagem intitulada Calcule a sequência de Fibonacci Passo 4

4. Conte o primeiro termo (1) e 0. juntos em. Isso lhe dará o segundo número na sequência.

Lembre-se que para encontrar um determinado número da sequência de Fibonacci, você só precisa somar os dois números anteriores.

Para criar a sequência, 0 vem antes de 1 (o primeiro termo), então: 1 + 0 = 1.

Imagem intitulada Calcule a sequência de Fibonacci Passo 5

5. Adicione o primeiro termo (1) e o segundo termo (1) juntos. Isso lhe dará o terceiro número na sequência.

1 + 1 = 2. O terceiro termo é 2.

Imagem intitulada Calcule a sequência de Fibonacci Passo 6

6. Adicione o segundo termo (1) e o terceiro termo (2) para obter o quarto número na sequência.

1 + 2 = 3. O quarto termo é 3.

Imagem intitulada Calcule a Sequência de Fibonacci Passo 7

7. Adicione o terceiro termo (2) e o quarto termo (3) juntos. Agora você sabe o quinto número na sequência.

2 + 3 = 5. O quinto termo é 5.

Imagem intitulada Calcule a Sequência de Fibonacci Passo 8

8. Some os dois números anteriores para encontrar qualquer número na sequência de Fibonacci. Se você usar este método, você usa a fórmula

f n = f_{n - 1} + f_{n - 2}

$F_{{n}}=F_{{n-1}}+F_{{n-2}}$ . Como esta não é uma fórmula fechada, você não pode usá-la para calcular todos os termos da série sem primeiro calcular todos os números anteriores.

Método 2 de 2: Usando a fórmula de Binet e a Média Dourada

Imagem intitulada Calcule a Sequência de Fibonacci Passo 9

1. Anote a fórmula:

X n

$x_{{n}}$ =

φ n - (1 - φ)^{n} \sqrt{5}

${frac{phi ^{{n}}-(1-phi)^{{n}}}{{sqrt{5}}}}$ . Na fórmula,

X n

$x_{{n}}$ = o termo na sequência que você está tentando encontrar,

n

$n$ = o número de posição do termo na série, e

φ

$phi$ = proporção áurea.

Esta é uma fórmula fechada, para que você possa calcular um termo específico da série sem precisar calcular todos os anteriores.
Esta fórmula é uma fórmula simplificada derivada da fórmula de Fibonacci de Binet.
A fórmula aplica a proporção áurea ( $φ$ $phi$ ), porque a proporção de dois números consecutivos na sequência de Fibonacci é muito semelhante à proporção áurea.

Imagem intitulada Calcule a Sequência de Fibonacci Passo 10

2. Ajuste o número para n{estilo de exibição n} $n$ aplicar na fórmula. O

n

$n$ representa o termo que você está procurando na sequência.

Por exemplo, se você estiver procurando pelo quinto número na sequência, digite 5. Sua fórmula agora deve ficar assim:

X 5

$x_{{5}}$ =

φ 5 - (1 - φ)^{5} \sqrt{5}

${frac{phi ^{{5}}-(1-phi)^{{5}}}{{sqrt{5}}}}$ .

Imagem intitulada Calcule a Sequência de Fibonacci Passo 11

3. Substitua a proporção áurea na fórmula. Use 1,618034 como uma aproximação da proporção áurea.

Por exemplo, se você pesquisar o quinto número na sequência, a fórmula que você inseriu ficaria assim:

X 5

$x_{{5}}$ =

(1, 618034) 5 - (1 - 1, 618034)^{5} \sqrt{5}

${frac{(1.618034)^{{5}}-(1-1,618034)^{{5}}}{{sqrt{5}}}}$ .

Imagem intitulada Calcule a Sequência de Fibonacci Passo 12

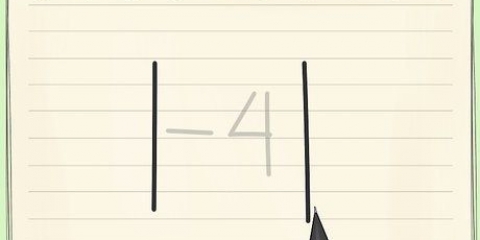
4. Complete os cálculos entre parênteses. Considere a ordem das operações aritméticas calculando primeiro a parte entre parênteses:

1 - 1, 618034 = - 0, 618034

$1-1,618034=-0,618034$ .

No exemplo, a equação se torna

X 5

$x_{{5}}$ =

(1, 618034) 5 - (- 0, 618034)^{5} \sqrt{5}

${frac{(1.618034)^{{5}}-(-0.618034)^{{5}}}{{sqrt{5}}}}$ .

Imagem intitulada Calcule a Sequência de Fibonacci Passo 13

5. Calcule os expoentes. Multiplique os dois números entre parênteses no numerador pelo expoente apropriado.

No exemplo,

1, 618034 5 = 11, 090170

$1,618034^{{5}}=11,090170$ ;

- 0, 618034 5 = - 0, 090169

$-0,618034^{{5}}=-0,090169$ . Então a equação fica

X 5 = 11, 090170 - (- 0, 090169) \sqrt{5}

$x_{{5}}={frac{11,090170-(-0.090169)}{{sqrt{5}}}}$ .

Imagem intitulada Calcule a Sequência de Fibonacci Passo 14

6. Complete o cálculo. Antes de continuar dividindo, você deve primeiro subtrair os dois números no numerador.

No exemplo,

11, 090170 - (- 0, 090169) = 11, 180339

$11,090170-(-0,090169)=11,180339$ , então a equação fica

X 5

$x_{{5}}$ =

11, 180339 \sqrt{5}

${frac{11,180339}{{sqrt{5}}}}$ .

Imagem intitulada Calcule a Sequência de Fibonacci Passo 15

7. Divida pela raiz quadrada de cinco. A raiz quadrada de cinco é arredondada para 2,236067.

Na atribuição de exemplo,

11, 180339 2, 236067 = 5, 000002

${frac{11,180339}{2,236067}}=5,000002$ .

Imagem intitulada Calcule a Sequência de Fibonacci Passo 16

8. Arredondar para o número inteiro mais próximo. Sua resposta é um número decimal, mas é muito próximo de um número inteiro. Este inteiro representa o número na sequência de Fibonacci.

Se você usou a proporção áurea completa e não arredondou nada, obterá um número inteiro. No entanto, é mais prático arredondar, o que resultará em um decimal.

No exemplo, sua resposta, calculada com uma calculadora, será de aproximadamente 5.000002. Arredondado para o número inteiro mais próximo, sua resposta será cinco, que também será o quinto número na sequência de Fibonacci.