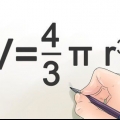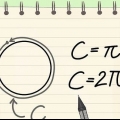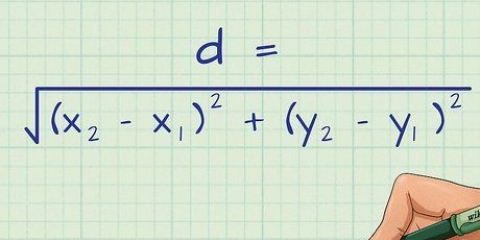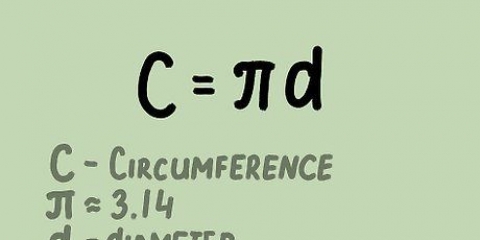Como Calcular o Raio de uma Esfera

Contente

Degraus
Pontas

O raio de uma esfera (abreviado como a variável r ou R) é a distância do centro exato da esfera a um ponto na superfície dessa esfera. Assim como círculos, o raio de uma esfera é frequentemente um primeiro dado essencial para o cálculo do diâmetro, circunferência, área e volume de uma esfera. No entanto, você também pode trabalhar para trás a partir do diâmetro, circunferência, etc. para encontrar o raio da esfera. Use a fórmula apropriada para os dados que você tem.

Degraus

Método 1 de 3: usando fórmulas de raio

Imagem intitulada Encontre o raio de uma esfera Passo 1

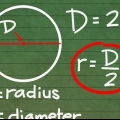
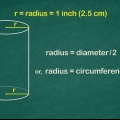
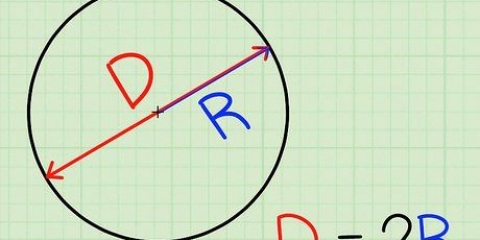
1. Determine o raio se você conhece o diâmetro. O raio é metade de um diâmetro, então você usa a fórmula r = D/2. Isto é idêntico ao método para calcular o raio de um círculo dado o diâmetro.

Se você tem uma esfera com um diâmetro de 16 cm, você calcula o raio com 16/2 = 8 cm. Se o diâmetro é 42, então o raio 21.

Imagem intitulada Encontre o raio de uma esfera Passo 2

2. Determine o raio se você conhece a circunferência. Use a fórmula C/2π. Como a circunferência é igual a πD, que por sua vez é igual a 2πr, você calcula o raio dividindo a circunferência por 2π.

Se você tem uma esfera com uma circunferência de 20 m, você encontrará o raio com 20/2π = 3,183 m.

A mesma fórmula pode ser usada para converter entre o raio e a circunferência de um círculo.

Imagem intitulada Encontre o raio de uma esfera Passo 3

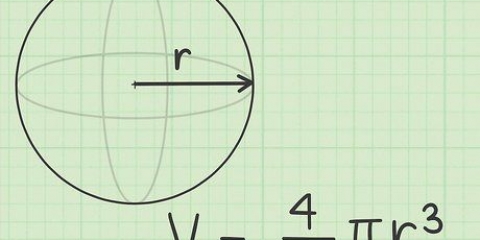
3. Calcule o raio se você conhece o volume da esfera. Use a fórmula ((V/π)(3/4)). O volume de uma esfera é derivado da equação V = (4/3)πr.Resolvendo a equação para r, você obtém ((V/π)(3/4)) = r, então fica claro que o raio de uma esfera é igual ao volume dividido por π, vezes 3/4 , elevado a a potência de 1/3 (ou raiz cúbica).

Se você tem uma esfera com um volume de 100 cm, obtém o raio da seguinte forma:

((V/π)(3/4)) = r

((100/π)(3/4)) = r

((31.83)(3/4)) = r

(23.87) = r

2,88 = r

Imagem intitulada Encontre o raio de uma esfera Passo 4

4. Determine o raio da superfície. Use a fórmula r = √(A/(4π)). A área de uma esfera é calculada usando a equação A = 4πr. Resolvendo a equação para r dá √(A/(4π)) = r, o que significa que o raio de uma esfera é igual à raiz quadrada de sua área dividida por 4π. Você também pode ligar (A/(4π)) a 1/2 para o mesmo resultado.

Se você tem uma esfera com uma área de 1200 cm, você calcula o raio da seguinte forma:

√(A/(4π)) = r

√(1200/(4π)) = r

√(300/(π)) = r

√(95,49) = r

9,77 centímetros = r

Método 2 de 3: Definindo termos-chave

Imagem intitulada Encontre o raio de uma esfera Passo 5

1. Conheça as dimensões básicas de uma esfera. O raio (r) é a distância do centro exato da esfera a qualquer ponto na superfície da esfera. Em geral, você pode encontrar o raio de uma esfera se souber seu diâmetro, circunferência, volume ou área.

Diâmetro (D): o comprimento da linha que passa pelo centro de uma esfera & ndash; dobro do raio. O diâmetro é o comprimento de uma linha que passa pelo centro da esfera: de um ponto do lado de fora da esfera a um ponto correspondente diretamente oposto a ela. Em outras palavras, a maior distância possível entre dois pontos na esfera.
Circunferência (C): a distância unidimensional ao redor da esfera em seu ponto mais largo. Em outras palavras, o perímetro da seção transversal circular de uma esfera cujo plano passa pelo centro da esfera.
Volume (V): o espaço tridimensional dentro da esfera. É o "espaço ocupado pela esfera".
Área (A): o espaço bidimensional na superfície externa da esfera. A quantidade de espaço plano que cobre a parte externa da esfera.
pi (π): uma constante que expressa a razão entre a circunferência do círculo e o diâmetro do círculo. Os primeiros 10 dígitos de Pi são sempre 3.141592653, embora isso seja geralmente arredondado para 3.14.

Imagem intitulada Encontre o raio de uma esfera Passo 6

2. Use leituras diferentes para determinar o raio. Você pode usar o diâmetro, perímetro, volume e área para calcular o raio de uma esfera. Se você conhece o comprimento do raio, pode calcular qualquer um desses números. Então, para encontrar o raio, você pode inverter as fórmulas para calcular essas partes. Aprenda as fórmulas que envolvem raio para calcular diâmetro, circunferência, área e volume.

D = 2r. Assim como círculos é o diâmetro de uma esfera duas vezes o seu raio.

C = πD ou 2πr. Assim como círculos é a circunferência de uma esfera igual a π vezes o diâmetro. Como o diâmetro é o dobro do raio, também podemos dizer que a circunferência é igual ao dobro do raio vezes π.

V = (4/3)πr. O volume de uma esfera é o seu raio ao cubo (r x r x r), vezes π, vezes 4/3.

A = 4πr. A área de uma esfera é o seu raio à segunda potência (r x r), vezes π, vezes 4. Como a circunferência de um círculo é igual a πr, também pode-se dizer que a área de uma esfera é igual a quatro vezes a área de um círculo, formada por sua circunferência.

Método 3 de 3: Encontrando o raio como a distância entre dois pontos

Imagem intitulada Encontre o raio de uma esfera Passo 7

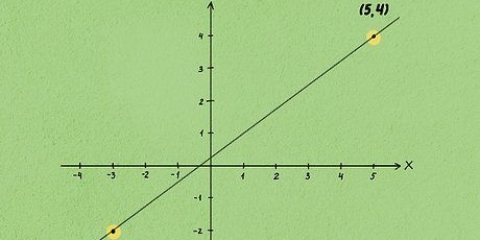
1. Determine as coordenadas (x, y, z) do centro da esfera. Uma maneira de pensar sobre o raio de uma esfera é como a distância entre o centro da esfera e qualquer ponto em sua superfície. Como isso é verdade, você pode determinar o raio da esfera usando as coordenadas do centro e um ponto na superfície da esfera, calculando a distância entre os dois pontos usando uma variante da fórmula de distância padrão. Para começar, encontre as coordenadas do centro da esfera. Observe que uma esfera é tridimensional, este será um ponto (x, y, z) em vez de um ponto (x, y).

Isso é mais fácil de entender com um exemplo. Suponha que uma esfera seja dada com centro(-1, 4, 12). Nos próximos passos vamos usar este ponto para determinar o raio.

Imagem intitulada Encontre o raio de uma esfera Passo 8

2. Determine as coordenadas de um ponto na superfície da esfera. Então você precisa determinar as coordenadas (x, y, z) de um ponto na superfície da esfera. Isso é possível cada ponto na superfície da esfera. Como, por definição, todos os pontos na superfície de uma esfera são equidistantes do centro, você pode usar qualquer ponto para determinar o raio.

No contexto de nossa atribuição de exemplo, afirmamos que o ponto (3, 3, 0) na superfície da esfera, é dado. Calculando a distância entre este ponto e o centro, podemos encontrar o raio.

Imagem intitulada Encontre o raio de uma esfera Passo 9

3. Determine o raio com a fórmula d = √((x₂ - X₁) + (s₂ - y₁) + (z₂ - z₁)). Agora que você conhece o centro da esfera e um ponto na superfície da esfera, você pode descobrir o raio calculando a distância entre eles. Use a fórmula de distância tridimensional d = √((x₂ - X₁) + (s₂ - y₁) + (z₂ - z₁)), onde d é a distância, (x₁,y₁,z₁) representa as coordenadas do ponto central, e(x₂,y₂,z₂) representa as coordenadas do ponto na superfície, para determinar a distância entre os dois pontos.

Em nosso exemplo, substituímos (4, -1, 12) por (x₁,y₁,z₁) e (3, 3, 0) para (x₂,y₂,z₂), onde resolvemos isso da seguinte forma:

d = √((x₂ - X₁) + (s₂ - y₁) + (z₂ - z₁))

d = √((3 - 4) + (3 - -1) + (0 - 12))

d = √((-1) + (4) + (-12))

d = √(1 + 16 + 144)

d = √(161)

d = 12,69. Este é o raio da nossa esfera.

Imagem intitulada Encontre o raio de uma esfera Passo 10

4. Saiba que, em geral, r = √((x₂ - X₁) + (s₂ - y₁) + (z₂ - z₁)). Em uma esfera, todos os pontos da superfície estão à mesma distância do centro da esfera. Vamos pegar a fórmula de distância tridimensional acima e substituir a variável "d" pela variável "r" do raio, então obtemos uma equação que nos permite encontrar o raio em qualquer centro dado (x₁,y₁,z₁) e qualquer ponto correspondente na superfície (x₂,y₂,z₂).

Ao elevar ao quadrado ambos os lados desta equação, obtemos: r = (x₂ - X₁) + (s₂ - y₁) + (z₂ - z₁). Nota: Isso é essencialmente equivalente à equação padrão para uma esfera (r = x + y + z), assumindo que seu centro é igual a (0,0,0).

Pontas

A ordem das operações importa. Se você não tem certeza de como as regras matemáticas funcionam e sua calculadora suporta parênteses, certifique-se de usar esses.
Este artigo foi criado porque este tópico estava em alta demanda. No entanto, se você está tentando entender a geometria espacial pela primeira vez, provavelmente é melhor começar pelo outro lado: calcular as propriedades de uma esfera quando seu raio é dado.
Pi ou π é uma letra grega que indica a razão entre o diâmetro de um círculo e sua circunferência. É um número irracional e não pode ser escrito como uma razão de números reais. Existem muitas aproximações, e 333/106 dá pi com quatro casas decimais. Hoje, a maioria das pessoas se lembra da aproximação 3,14, que geralmente é precisa o suficiente para fins diários.