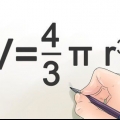Calculando a Massa de uma Esfera: 13 Passos (com Imagens)

Contente

Degraus
Pontas

Simplificando, uma esfera é uma bola redonda sólida. Para calcular a massa de uma esfera, você precisa saber o tamanho (volume) da esfera e sua densidade. Você pode calcular o volume usando o raio, circunferência ou diâmetro da esfera. Você também pode submergir a esfera em água para encontrar o volume por deslocamento de água. Se você conhece o volume, pode multiplicá-lo pela densidade para encontrar a massa.

Degraus

Parte 1 de 3: Determinando o volume de uma esfera

Imagem intitulada Calcular a massa de uma esfera Passo 1

1. Use a formula do volume de uma esfera. Uma esfera é um sólido circular em três dimensões. A fórmula primária para o volume de uma esfera é:

$Volume = \frac{4}{3} π r^{3}$ ${displaystyle {text{Volume}}={frac {4}{3}}pi r^{3}}$

$π = 3, 14$ ${estilo de exibição pi =3.14}$
$r = raio$ ${displaystyle r={text{raio}}}$

Imagem intitulada Calcule a massa de uma esfera Passo 2

2. Encontre o volume de uma esfera se você conhece seu raio. O raio de uma esfera é a medida do centro da esfera até a borda externa. Se você tiver um problema para calcular o volume, então o raio provavelmente é dado. Caso contrário, o raio pode ser difícil de medir porque você não pode determinar com precisão o centro de um objeto sólido.

Suponha que lhe digam que existe uma esfera com um raio de 10 cm. Encontre o volume da seguinte forma:

Volume = \frac{4}{3} π r^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi r^{3}}$

Volume = \frac{4}{3} * (3, 14) * 10^{3}

${displaystyle {text{Volume}}={frac {4}{3}}*(3.14)*10^{3}}$

Volume = 4, 18667 * 1000

${displaystyle {text{Volume}}=4.18667*1000}$

Volume = 4186, 67 {cm}^{3}

${displaystyle {text{Volume}}=4186,67{text{cm}}^{3}}$

Imagem intitulada Calcule a massa de uma esfera Passo 3

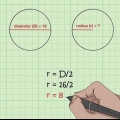
3. Determine o volume se o diâmetro for especificado. Outra possibilidade é que para uma determinada situação o diâmetro de uma esfera seja dado. O diâmetro é igual ao dobro do raio. Na verdade, o diâmetro é a distância de uma borda da esfera através do centro até a outra borda. Para calcular o volume a partir do diâmetro (d), revise a fórmula da seguinte forma:

Volume = \frac{4}{3} π (\frac{d}{2})^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi ({frac {d}{2}})^{3}}$

Como exemplo deste cálculo, determine o volume de uma esfera com diâmetro de 10 cm.

Volume = \frac{4}{3} π (\frac{d}{2})^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi ({frac {d}{2}})^{3}}$

Volume = \frac{4}{3} π (\frac{10}{2})^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi ({frac {10}{2}})^{3}}$

Volume = \frac{4}{3} * (3, 14) * (5^{3})

${displaystyle {text{Volume}}={frac {4}{3}}*(3.14)*(5^{3})}$

Volume = 4, 18667 * 125

${displaystyle {text{Volume}}=4.18667*125}$

Volume = 523, 3 {cm}^{3}

${displaystyle {text{Volume}}=523.3{text{cm}}^{3}}$

Imagem intitulada Calcule a massa de uma esfera Passo 4

4. Revise a fórmula se você conhece o perímetro. A circunferência de uma esfera é provavelmente a mais fácil de medir diretamente. Você pode usar uma fita métrica, enrolá-la suavemente ao redor da parte mais larga da lâmpada e tirar a medida. Talvez a circunferência seja dada em uma declaração. Para encontrar o volume começando com o perímetro (C), revise a fórmula da seguinte forma:

Volume = \frac{4}{3} π r^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi r^{3}}$

Volume = \frac{4}{3} π * (C 2 π)^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi *({frac {C}{2pi }})^{3}}$

Volume = \frac{4}{3} π * (C 3 8 π 3)

${displaystyle {text{Volume}}={frac {4}{3}}pi *({frac {C^{3}}{8pi ^{3}}})}$

Volume = C 3 6 π 2

${displaystyle {text{Volume}}={frac {C^{3}}{6pi ^{2}}}}$

Imagem intitulada Calcule a massa de uma esfera Passo 5

5. Calcule o volume se você conhece o perímetro. Suponha que você pegue uma esfera e meça a circunferência em 32 cm. Encontre o volume da seguinte forma:

Volume = C 3 6 π 2

${displaystyle {text{Volume}}={frac {C^{3}}{6pi ^{2}}}}$

Volume = 323 6 * 3, 14 2

${displaystyle {text{Volume}}={frac {32^{3}}{6*3.14^{2}}}}$

Volume = 32.768 59, 158

${displaystyle {text{Volume}}={frac {32.768}{59.158}}}$

Volume = 553, 9 {cm}^{3}

${displaystyle {text{Volume}}=553,9{text{cm}}^{3}}$

Imagem intitulada Calcule a massa de uma esfera Passo 6

6. Medir o volume por deslocamento de água. Um método final e prático de medir o volume é mergulhar o bulbo em água. Você deve ter um béquer grande o suficiente para submergir a lâmpada com marcações de volume precisas.

Despeje água suficiente no copo para cobrir o bulbo. Observe o volume.

Despeje o bulbo na água. Observe que o nível da água está subindo. Observe o novo volume.

Subtraia o primeiro volume do segundo. O resultado é o volume da esfera.

Suponha que seu nível de água suba de 100ml para 625ml quando você submergir a lâmpada. Então o volume é 525 ml. Observe que 1 ml = 1 cm.

Parte 2 de 3: Calculando a massa a partir do volume

Imagem intitulada Calcule a massa de uma esfera Passo 7

1. Determine a densidade. Para calcular a massa do volume, você precisa saber a densidade do objeto. Diferentes materiais têm diferentes densidades. Por exemplo, considere uma esfera de isopor e compare seu peso com uma esfera do mesmo tamanho de ferro. O ferro tem uma densidade muito maior e, portanto, terá uma massa maior.

Você pode procurar densidades de muitos materiais sólidos online, em livros didáticos ou em uma Binas.
Por exemplo, aqui estão as densidades registradas de alguns materiais sólidos:

Alumínio = 2700 kg/m
Manteiga = 870 kg/m
Chumbo = 11.350kg/m
Madeira prensada = 190 kg/m

Imagem intitulada Calcule a massa de uma esfera Passo 8

2. Converta as unidades conforme necessário. As unidades que você usa ao calcular o volume devem corresponder às unidades de volume na densidade medida. Se não, então você tem que convertê-los.

Todos os exemplos da seção anterior resultaram em volumes medidos em centímetros cúbicos. No entanto, a tabela de densidade indicada fornece densidades baseadas em metros cúbicos. Porque existem 100 centímetros em um metro, existem 10 centímetros cúbicos em um metro cúbico. Divida as densidades dadas por 10 para obter a densidade em unidades de kg/cm (facilmente feito movendo a vírgula seis espaços para a esquerda).

Para os quatro materiais listados anteriormente, as densidades convertidas são as seguintes:

Alumínio = 2700 kg/m = 0,0027 kg/cm

Manteiga = 870 kg/m3 = 0,00087 kg/cm

Chumbo = 11.350 kg/m = 0,01135 kg/cm

Madeira prensada = 190 kg/m = 0,00019 kg/cm

Imagem intitulada Calcule a massa de uma esfera Passo 9

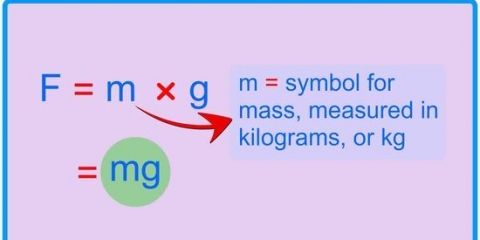
3. Multiplique o volume pela densidade para encontrar a massa. A fórmula da densidade é

Densidade = \frac{Massa}{Volume}

${displaystyle {text{Densidade}}={frac {text{Mass}}{text{Volume}}}}$ , como você pode se lembrar. Se você reorganizar isso para encontrar a massa, a equação se torna

Densidade * Volume = Massa

${displaystyle {text{Densidade}}*{text{Volume}}={text{Mass}}}$ .

Usando os quatro materiais mencionados anteriormente, alumínio, manteiga, chumbo e madeira prensada, você determina a massa de uma esfera com volume de 500 cm.

Alumínio : 500 {cm}^{3} * 0, 0027 \frac{kg}{} cm 3 = 1, 35 kg

${displaystyle {text{Alumínio}}:500{text{ cm}}^{3}*0.0027{frac {text{kg}}{{text{cm}}^{3}} }= 1,35{text{ kg}}}$

Manteiga : 500 {cm}^{3} * 0, 00087 \frac{kg}{} cm 3 = 0, 435 kg

${displaystyle {text{Butter}}:500{text{ cm}}^{3}*0.00087{frac {text{kg}}{{text{cm}}^{3}} }= 0,435{text{ kg}}}$

Liderar : 500 {cm}^{3} * 0, 01135 \frac{kg}{} cm 3 = 5, 675 kg

${displaystyle {text{Lead}}:500{text{ cm}}^{3}*0.01135{frac {text{kg}}{{text{cm}}^{3}} }= 5.675{text{ kg}}}$

Madeira prensada : 500 {cm}^{3} * 0, 00019 \frac{kg}{} cm 3 = 0, 095 kg

${displaystyle {text{Pressed Wood}}:500{text{ cm}}^{3}*0.00019{frac {text{kg}}{{text{cm}}^{3} }} =0,095{text{ kg}}}$

Parte 3 de 3: Resolvendo um problema de amostra

Imagem intitulada Calcule a massa de uma esfera Passo 10

1. Leia a tarefa com atenção. Ao responder a problemas com cálculos de massa, leia toda a declaração com atenção. Enquanto você lê, pode ajudar a destacar a entrada. Leia todo o problema cuidadosamente para ver o que você será solicitado a resolver. Por exemplo, considere o seguinte problema:

Uma grande esfera de latão maciço tem um diâmetro de 1,2 m. Determine a massa da esfera.

Imagem intitulada Calcular a massa de uma esfera Passo 11

2. Organize os dados conhecidos e desconhecidos. Se você ler a declaração com atenção, poderá determinar que o diâmetro é fornecido, portanto, use a fórmula modificada:

Volume = \frac{4}{3} π (\frac{d}{2})^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi ({frac {d}{2}})^{3}}$

Você também leu que a esfera é feita de latão. Você precisa procurar a densidade do latão em suas Binas ou de outra fonte.

No site, EngineeringToolbox.com, você pode ver que a densidade do latão é 8480 kg/m. Como o diâmetro da esfera é dado em metros, seu volume é calculado em metros cúbicos, então você não precisa converter a densidade.

Imagem intitulada Calcule a massa de uma esfera Passo 12

3. Calcule o volume. Para calcular o volume, insira a fórmula apropriada, preencha os dados que você conhece e execute os cálculos da seguinte forma:

Volume = \frac{4}{3} π (\frac{d}{2})^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi ({frac {d}{2}})^{3}}$

Volume = \frac{4}{3} π (1, 2 2)^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi ({frac {1,2}{2}})^{3}}$

Volume = 4, 18667 * 0, 6^{3}

${displaystyle {text{Volume}}=4.18667*0.6^{3}}$

Volume = 4, 18667 * 0, 216

${displaystyle {text{Volume}}=4.18667*0.216}$

Volume = 0, 90432 m^{3}

${displaystyle {text{Volume}}=0.90432{text{ m}}^{3}}$

Imagem intitulada Calcule a massa de uma esfera Passo 13

4. Use a densidade para calcular a massa. Pense nisso

Massa = Densidade * Volume

${displaystyle {text{Mass}}={text{Densidade}}*{text{Volume}}}$ . Insira os valores que você conhece na fórmula para encontrar a massa:

Massa = Densidade * Volume

${displaystyle {text{Mass}}={text{Densidade}}*{text{Volume}}}$

Massa = 8480 \frac{kg}{} m 3 * 0, 90432 m^{3}

${displaystyle {text{Mass}}=8480{frac {text{ kg}}{{text{ m}}^{3}}}*0.90432{text{ m}}^{3 }}$

Massa = 7668, 6 kg

${displaystyle {text{Mass}}=7668,6{text{ kg}}}$

Pontas

Esta explicação assume que a densidade da esfera é a mesma em todos os lugares. Isso é assumido na maioria dos problemas matemáticos e físicos. No entanto, é possível que o núcleo de uma esfera seja feito de material diferente da superfície.