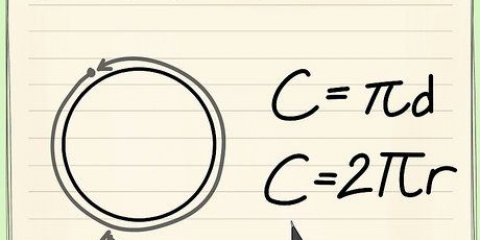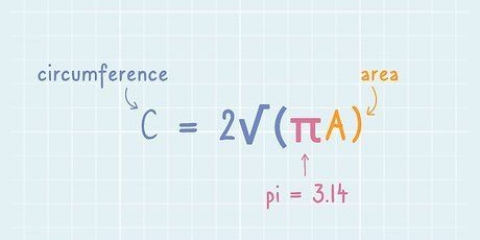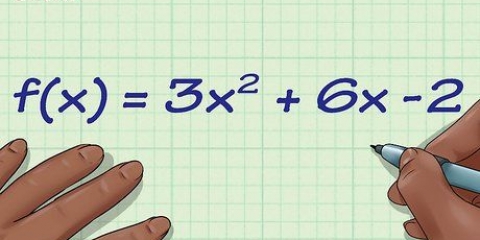Dicas para usuários avançados: Se você conhece apenas o volume de uma esfera, precisa trabalhar um pouco mais para obter o raio. Divida o volume por 4π e multiplique essa resposta por 3. Finalmente, tire a raiz cúbica desta resposta. 

Se nosso raio for 5, como acima, você ficará com 4 x 25 x π, ou 100π. 
100 x = 100 x 3,14 100π = 314 
A resposta completa para a esfera nas fotos é: Área = 314 unidades. As unidades que você usa são sempre os mesmos usados para medir o raio. Se o raio estiver em metros, a resposta também estará em metros. Dica avançada: Nós elevamos as unidades ao quadrado porque a área mede quantos quadrados planos cabem na superfície da esfera. Suponha que medimos o problema do exercício em cm. Isso significa que em uma esfera onde r = 5, poderíamos encaixar 314 quadrados na superfície da esfera, se os lados de cada quadrado tivessem 1 cm de comprimento. 
4πr r = 7 4xx7 49x4x 196π Responder: Área = 615,75 cm (centímetros quadrados). 
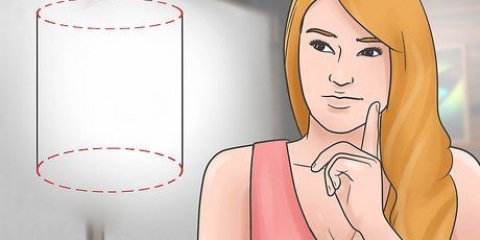
A rotação de um círculo em torno de seu eixo (o centro) produz uma esfera. Pense em girar uma moeda na mesa e como ela parece formar uma esfera. Embora não seja explicado aqui, é daí que vem nossa comparação. Dicas para usuários avançados: As esferas têm uma área de superfície menor por volume do que qualquer outra forma - isso significa que elas podem conter mais coisas por área de superfície do que qualquer outra forma.
Determinando a área de uma esfera
A área de uma esfera é o número de unidades quadradas (cm, centímetros quadrados ou metros - qualquer que seja sua medida) que cobrem a parte externa de um objeto esférico. A equação foi descoberta há milhares de anos pelo filósofo e matemático grego Aristóteles e relativamente simples (mesmo que sua origem não seja). Para encontrar a área de uma esfera, use a fórmula (4πr), onde r é o raio do círculo.
Degraus

1. Conheça as partes da equação (Área = 4πr). Esta fórmula antiga ainda é a maneira mais fácil de determinar a área de uma esfera. Usando quase qualquer calculadora, você pode preencher o raio para obter a área da sua esfera.
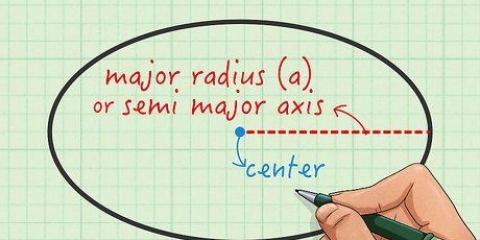
- r ou `raio:` O raio é a distância do centro da esfera até a borda da esfera.
- π ou `pi:` Esse número incrível (equivalente a aproximadamente 3,14) representa a razão entre a circunferência e o diâmetro de um círculo e é útil em todas as equações que envolvem círculos e esferas. Geralmente é abreviado para π = 3,1416, mas há um número infinito de casas decimais.
- 4: Por motivos um tanto complicados, a área de uma esfera é sempre 4 vezes a área de um círculo de mesmo raio.

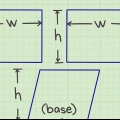
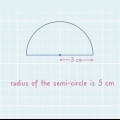
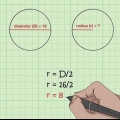
2. Determine o raio da esfera. Às vezes o problema te dá o raio e outras vezes você tem que encontrar você mesmo. Para obter o diâmetro de um círculo, basta dividir o diâmetro por 2, para obter o raio. Por exemplo: uma esfera com um diâmetro de 10 cm tem um raio de 5 cm.

3. Quadrado do raio multiplicando-o por ele mesmo. Você pode fazer isso por multiplicação manual (5 = 5 x 5 = 25) ou usando a função quadrada da calculadora (às vezes chamada de `x`).

4. Multiplique este resultado por 4. Embora você possa multiplicar 4 ou pi primeiro, geralmente é mais fácil começar com 4 porque ainda não há casas decimais para multiplicar.

5. Multiplique os resultados por pi (π). Se o problema fala sobre um `valor exato`, escreva o símbolo π após o seu número e pronto. Caso contrário, use a aproximação π=3,14 ou o botão π em sua calculadora.

6. Não se esqueça de escrever suas unidades após a resposta final. Deve ficar claro se a superfície da sua esfera é, por exemplo, 314 cm ou 314 km. A unidade deve ser escrita como "unidade", pois denota área, também conhecida como "unidades quadradas",

7. Pratique com um exemplo. Se o raio de uma esfera é 7 cm, qual é a área dessa esfera??

8. Compreender a área. A área de uma esfera é a área que cobre a parte externa da esfera - pense nela como o couro de uma bola de futebol ou a superfície da terra. Como uma esfera é curva, é muito mais difícil medir a área de uma esfera do que de uma caixa, por isso precisamos de uma equação para determinar a área.
Pontas
- Se o raio contiver uma raiz quadrada, como 3 √ 5, lembre-se de incluir os quadrados dos coeficientes E se ao quadrado da raiz. (3 √ 5) torna-se 9 x 5 = 45.
Artigos sobre o tópico "Determinando a área de uma esfera"
Оцените, пожалуйста статью
Popular