Ângulos retos são frequentemente indicados em livros didáticos e testes com um pequeno quadrado no canto direito. Esta marcação especial significa "90 graus." 
Se o seu triângulo tem lados de 3 e 4, e você atribuiu letras a esses lados de modo que a = 3 e b = 4, você resolve a equação como: 3 + 4 = c. 
Se a = 3, a = 3 x 3 ou 9.Se b = 4, então b = 4 x 4, ou 16. Quando você fatorar esses valores em sua equação, agora deve ficar assim: 9 + 16 = c. 
Em nosso exemplo, 9 + 16 = 25, tome nota então 25 = c. 
Em nosso exemplo, c = 25.A raiz quadrada de 25 é 5 (5 x 5 = 25, assim Sqrt(25) = 5).E isso significa c = 5, o comprimento da nossa hipotenusa! 

Você calcula a hipotenusa desse triângulo com base no comprimento de um dos catetos e multiplica seu comprimento por Sqrt(2). É útil conhecer essa proporção, especialmente se seus problemas de teste ou lição de casa fornecerem os comprimentos dos lados na forma de variáveis em vez de números inteiros. 
Dado o comprimento do cateto mais curto (o oposto ao ângulo de 30 graus), multiplique o comprimento desse cateto por 2 para obter o comprimento da hipotenusa. Por exemplo, se o comprimento da perna mais curta 4 é, então você sabe que a hipotenusa 8 devemos ser. Se você souber o comprimento da perna mais longa (oposto ao ângulo de 60 graus), multiplique esse comprimento por2/Quadrado(3) para encontrar o comprimento da hipotenusa.Por exemplo, se o comprimento da perna mais curta 4 é, então você sabe que a hipotenusa 4,62 devemos ser. 

Para encontrar o seno de um ângulo de 80 graus, você pecado 80 deve digitar seguido do sinal de igual ou Enter, ou80 pecado. (A resposta é -0,9939.) Você também pode pesquisar "calculadora de pecados" com seu navegador para algumas calculadoras fáceis de usar para que você não precise adivinhar. 
A regra do seno pode, de fato, ser usada para resolver cada triângulo, mas apenas um triângulo retângulo terá uma hipotenusa. 

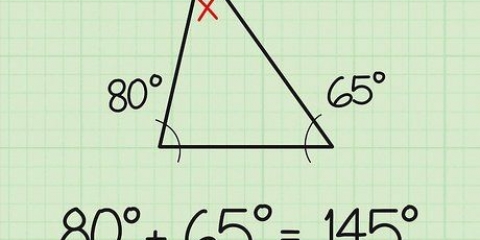
Por exemplo, se você sabe que A = 40 graus, então B = 180 – (90 + 40). Simplifique isso para B = 180 - 130 e você pode deduzir rapidamente que B = 50 graus. 
Para continuar com nosso exemplo, digamos que o comprimento do lado a = 10.Ângulo C = 90 graus, ângulo A = 40 graus e ângulo B = 50 graus. 

A partir do nosso exemplo, vemos que pecado 40 = 0,64278761.Para encontrar o valor de c, dividimos o comprimento de a por esse número e descobrimos que 10 / 0,64278761 = 15,6, o comprimento da nossa hipotenusa!
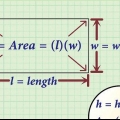
Determinando o comprimento da hipotenusa
Contente
Todos os triângulos retângulos têm um ângulo reto (de 90 graus), e a hipotenusa é o lado oposto a esse ângulo. A hipotenusa é o lado mais longo do triângulo e também é muito fácil de encontrar usando vários métodos diferentes. Este artigo irá ensiná-lo a determinar o comprimento da hipotenusa usando o Teorema de Pitágoras, desde que você conheça o comprimento dos outros dois lados do triângulo. Então você aprenderá como calcular a hipotenusa de alguns triângulos retângulos especiais que você encontrará frequentemente em testes. E, finalmente, você aprenderá a calcular o comprimento da hipotenusa usando a regra do seno, quando apenas o comprimento de um dos lados é conhecido e a magnitude de um dos ângulos é conhecida.
Degraus
Método 1 de 3: Usando o Teorema de Pitágoras

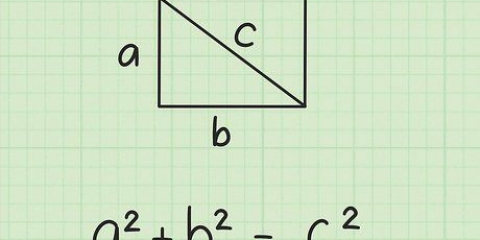
1. Aprenda o Teorema de Pitágoras. O Teorema de Pitágoras descreve a relação entre os lados de um triângulo retângulo. Ela afirma que para um triângulo retângulo arbitrário com lados a e b, e hipotenusa de comprimento c, temos a + b = c.

2. Verifique se o seu triângulo é um triângulo retângulo.O Teorema de Pitágoras só funciona para triângulos retângulos e, por definição, apenas um triângulo retângulo pode ter uma hipotenusa.Se o seu triângulo contém um ângulo de exatamente 90 graus, então é um triângulo retângulo e você pode continuar.

3. Atribua as variáveis a, b e c aos lados do seu triângulo.A variável "c" é sempre atribuído à hipotenusa, ou seja, o lado mais longo.Escolha um dos outros lados para o uma, e nomeie o lado restante b (não importa qual, a matemática continua a mesma).Em seguida, processe os comprimentos de a e b na fórmula, conforme mostrado no exemplo a seguir:

4. Determine os quadrados de a e b.Para encontrar o quadrado de um número, basta multiplicar esse número por ele mesmo, então a = a x a. Encontre os quadrados de a e b, e incorpore-os na fórmula.

5. Conte os valores deuma e b juntos em. Fatore isso em sua equação, e isso lhe dará o valor de c. Agora só falta um passo, e você determinou a hipotenusa!

6. Determine a raiz quadrada de c. Use a função raiz quadrada em sua calculadora (ou tabuada, se você souber de cor) para encontrar a raiz quadrada de c. A resposta é o comprimento da sua hipotenusa!
Método 2 de 3: Determinando a hipotenusa de triângulos retângulos especiais

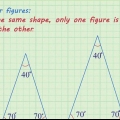
1. Aprenda a reconhecer os triângulos de um trio pitagórico. Os comprimentos dos lados de uma tríade de Pitágoras são inteiros obedecendo ao Teorema de Pitágoras. Você encontrará regularmente esses triângulos especiais em livros didáticos de geometria e em testes padrão, como o SAT e o GRE.Em particular, se você memorizar as 2 primeiras tríplices pitagóricas, você pode economizar muito tempo nesses testes porque você conhece imediatamente a hipotenusa de qualquer um desses triângulos apenas olhando para os comprimentos dos lados!
- O primeiro trio pitagórico é 3-4-5 (3 + 4 = 5, 9 + 16 = 25).Quando você vê um triângulo retângulo com lados de comprimento 3 e 4, você sabe imediatamente com certeza que a hipotenusa será 5 sem ter que fazer nenhum cálculo.
- A razão de uma tripla pitagórica permanece a mesma mesmo quando os lados são multiplicados por um número diferente. Por exemplo: um triângulo retângulo com lados 6 e 8 terá uma hipotenusa de 10 (6 + 8 = 10, 36 + 64 = 100).O mesmo se aplica a9-12-15, até 1,5-2-2,5.Faça os cálculos e você verá!
- O segundo trio pitagórico que você encontrará frequentemente em testes é 5-12-13 (5 + 12 = 13, 25 + 144 = 169).Cuidado também com os plurais, como 24-10-26 e 2,5-6-6,5.

2. Aprenda a razão dos lados de um triângulo retângulo com ângulos 45-45-90. Um triângulo retângulo 45-45-90 tem ângulos de 45, 45 e 90 graus, e também é chamado de triângulo retângulo isósceles. Este é frequentemente encontrado em testes padrão e é um triângulo muito fácil de resolver. A razão entre os lados desse triângulo é 1:1: Quadrado(2), o que significa que o comprimento dos catetos é igual, e o comprimento da hipotenusa é então simplesmente o comprimento dos catetos multiplicado pela raiz quadrada de dois.

3. Aprenda as proporções de um triângulo de ângulo reto 30-60-90. Este triângulo tem ângulos de 30, 60 e 90 graus e pode ser feito dividindo um triângulo equilátero ao meio. Os lados do triângulo retângulo 30-60-90 sempre têm a razão 1: Quadrado(3):2, ou x:Sqrt(3)x:2x.Se for dado o comprimento de um cateto do triângulo 30-60-90 e solicitado a determinar a hipotenusa, é muito fácil fazer:
Método 3 de 3: Calculando a hipotenusa com a regra do seno

1. Entenda o que o "Seio" meios. Os termos "seio," "cosseno" e "tangente" todos se referem a certas proporções entre os ângulos e/ou lados de um triângulo retângulo.Em um triângulo retângulo, é seio de um ângulo definido como o comprimento do lado oposto ao ângulo dividido por a hipotenusa do triângulo. A abreviatura para seno como aparece na sua calculadora é pecado.

2. Aprenda a calcular o seno. Mesmo uma calculadora científica simples tem uma função seno. Olhe para a chave marcada pecado.Para encontrar o seno de um ângulo, você geralmente pressiona o botão pecado-tecla e, em seguida, digite o ângulo em graus.No entanto, em algumas calculadoras, você deve primeiro inserir o ângulo em graus e depois pressionar o botão pecado-Aperte o botão. Você terá que experimentar com sua calculadora ou procurar no manual para determinar qual é.

3. Aprenda a regra do seno.A regra do seno é uma ferramenta útil para resolver problemas de triângulo. Você pode usá-lo principalmente para encontrar a hipotenusa de um triângulo retângulo, se você souber o comprimento de um lado e um de seus ângulos diferentes do ângulo reto. Para qualquer triângulo com lados uma, b e c e os cantos uma, B e C, a regra do seno diz que uma / pecado uma = b/ pecado B = c/ pecado C.

4. Atribua as variáveis a, b e c aos lados do seu triângulo. A hipotenusa (o lado maior) deve ser sempre o "c" são. Para simplificar, rotule o lado de comprimento conhecido como "uma" e outros "b". Em seguida, atribua as variáveis A, B e C aos cantos do triângulo. O ângulo reto oposto à hipotenusa torna-se então "C".O canto oposto "uma" é ângulo "uma" e o ângulo lado oposto "b" é "B".

5. Calcule o terceiro ângulo. Porque é um ângulo reto você já sabe disso C = 90 graus e você também sabe o ângulo uma ou B é. Como a soma de todos os ângulos em um triângulo deve sempre ser igual a 180 graus, é fácil calcular o terceiro ângulo usando a fórmula: 180 – (90 + A) = B. Você também pode inverter esta equação para que 180 – (90 + B) = A.

6. Examine seu triângulo.Neste ponto você conhece todos os ângulos do triângulo e o comprimento do lado a. Agora é hora de processar esses valores na Regra do Seno, para calcular o comprimento dos outros dois lados.

7. Aplique a Regra do Seno ao seu triângulo.Nós só precisamos processar nossos números e resolver a seguinte equação, para encontrar o comprimento da hipotenusa c: comprimento do lado a/ pecado A = comprimento do lado c/ pecado C.Isso ainda pode parecer um pouco intimidante, mas o seno de 90 graus é uma constante e sempre é igual a 1!Portanto, nossa equação pode ser simplificada para: uma / pecado A = c/1, ou mais simples uma / pecado A = c.

8. Divida o comprimento da sedauma pelo seno do ângulo uma para encontrar o comprimento da hipotenusa!Você pode calcular isso em duas etapas separadas, primeiro: pecado Calcule e escreva A, depois divida por a. Ou teste tudo de uma vez na sua calculadora. Se você fizer isso, não esqueça os parênteses após o sinal de divisão.Por exemplo, digite 10 / (pecado 40) ou 10 / (40 pecado), dependendo da sua calculadora.
Artigos sobre o tópico "Determinando o comprimento da hipotenusa"
Оцените, пожалуйста статью
Similar
Popular