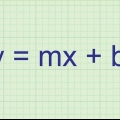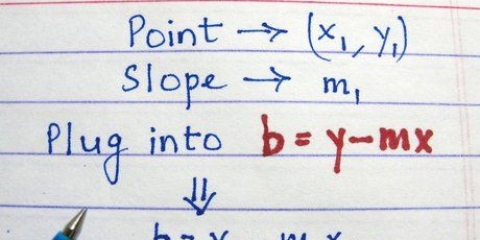(3-5)/(8-2) = -2/6 = -1/3 A inclinação da linha é -1/3. Para encontrar essa inclinação, você precisa simplificar 2/6 para seus menores valores, 1/3, já que 2 e 6 são divisíveis por 2. 
O recíproco negativo de -1/3 é 3 porque 3/1 é o recíproco de 1/3 e o sinal mudou de negativo para positivo. 

3 --> y = mx + b = y = 3x + b 
(5, 4) --->y = 3x + b = 4 = 3(5) + b = 4 = 15 + b 
4 = 15 + b = -11 = b b = -11 
y = mx + b y = 3x - 11 A equação da mediatriz através dos pontos (2, 5) e (8, 3) é y = 3 x - 11.
Determinando a mediatriz de dois pontos
A mediatriz é uma linha que corta um segmento conectado por dois pontos em um ângulo de 90 graus. Para encontrar a mediatriz de dois pontos, tudo que você precisa fazer é encontrar seus pontos médios e a recíproca, então aplicar as respostas à equação de uma linha da forma y = mx + b. Se você quiser saber como encontrar a mediatriz de dois pontos, siga os passos abaixo.
Degraus
Método 1 de 2: coletar informações

1. Encontre o centro dos dois pontos. Encontre o ponto médio de dois pontos aplicando os pontos à fórmula do ponto médio: [(X1 + X2)/2,(1 + y2)/2]. Isso significa que você calcula a média das coordenadas xey dos dois pontos, o que lhe dá o centro das duas coordenadas. Suponha que trabalhamos com as coordenadas (x1, y1) de (2, 5) e as coordenadas (x2, y2) de (8, 3). Você determina o centro dos dois pontos da seguinte forma:
- [(2+8)/2, (5 +3)/2] =
- (2/10, 2/8) =
- (5, 4)
- As coordenadas do centro de (2, 5) e (8, 3) são (5, 4).

2. Encontre a inclinação dos dois pontos. Para encontrar a inclinação (inclinação) dos dois pontos, aplique os pontos à fórmula da inclinação: (s2 - y1) / (x2 - X1). A inclinação de uma linha é a distância de uma mudança vertical sobre a distância de uma mudança horizontal correspondente. Você determina a inclinação da linha através dos pontos (2, 5) e (8, 3) da seguinte forma:

3. Encontre o inverso negativo da inclinação dos dois pontos. Para encontrar o recíproco negativo de uma inclinação, pegue o recíproco da inclinação e mude o sinal. Você pode encontrar o recíproco de um número invertendo as coordenadas x e y. O recíproco negativo de 1/2 é -2/1, ou apenas -2; o recíproco de -4 é 1/4.
Método 2 de 2: Calcule a equação da reta

1. Escreva a equação de uma reta na forma y = mx + b. A equação de uma reta que passa por dois pontos é da forma `y = mx + b ` onde as coordenadas x e y na linha são representadas por `x` e `y`, o `m` representa a inclinação da linha e o `b` representa a interseção da linha com o eixo y. Depois de escrever esta equação, você pode começar a encontrar a equação da mediatriz dos dois pontos.

2. Aplique o recíproco negativo da inclinação original à equação. O recíproco negativo da inclinação dos pontos (2, 5) e (8, 3) foi 3. O `m` na equação representa a inclinação, então digite 3 para o `m` na equação de uma linha reta, y = mx + b.

3. Aplique o ponto médio à linha. Você já sabe que os pontos médios dos pontos (2, 5) e (8, 3) são iguais a (5, 4). Como a mediatriz passa pelos pontos médios das duas linhas, você pode aplicar as coordenadas dos pontos médios à equação da linha. Basta preencher (5, 4) no lugar das coordenadas x e y da linha.

4. Resolva a interseção. Você encontrou três das quatro variáveis na equação da reta. Agora você tem informações suficientes para determinar a variável restante `b`, a interseção desta linha com o eixo y. Isole a variável `b` para determinar seu valor. Subtraia 15 de ambos os lados da equação.

5. Escreva a equação da mediatriz. Para escrever a equação da mediatriz, substitua a inclinação da linha (3) e a interseção com o eixo y (-11) na equação da forma y = mx + b. Não insira nada para as coordenadas x e y, pois com esta equação você pode encontrar qualquer coordenada na linha preenchendo uma coordenada x ou y.
Artigos sobre o tópico "Determinando a mediatriz de dois pontos"
Оцените, пожалуйста статью
Similar
Popular