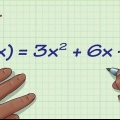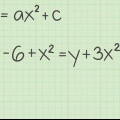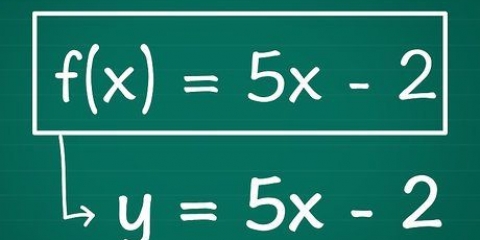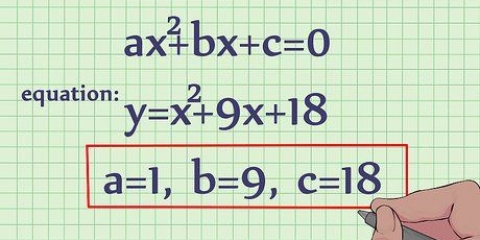Se o valor de uma é positivo, então você obtém o valor mínimo, porque a parábola no topo é aberta (o vértice é o ponto mais baixo do gráfico).
Se o valor de uma for negativo, você encontrará o valor máximo, pois a parábola na parte inferior é aberta (o vértice é o ponto mais alto do gráfico).
O valor de uma não pode ser zero, caso contrário não estamos lidando com uma equação quadrática, certo?







Determinando os valores máximo e mínimo de uma função quadrática
Contente
A coordenada y da crista ou vale de uma parábola (geralmente representada por k) também é o valor máximo ou mínimo da equação quadrática representada pela parábola. Vamos ver como determiná-lo!
Degraus
Método 1 de 4: Para uma equação quadrática da forma y = ax + bx + c

1. Decida se você deseja determinar o valor máximo ou o valor mínimo. É um ou outro, você não pode fazer os dois.
- O valor máximo ou mínimo de uma equação quadrática é o mesmo que o pico ou vale dessa função.
A função y = ax + bx + c,
(c - b/4a) retorna o valor y (o valor da função) como o vértice.




Método 2 de 4: Para uma equação quadrática na forma y = a(x-h) + k

1. Para y = a(x-h) + k, k é o valor da função no vértice.
- k nos dá o valor máximo ou mínimo da equação quadrática quando uma é negativo ou positivo respectivamente.

Método 3 de 4: Diferencie em uma equação quadrática da forma y = ax^2 + bx + c

1. Diferencie y para x. dy/dx = 2ax + b

2. Determine quais são os valores derivados em termos de dy/dx. Como dy/dx é a função derivada de uma curva, a derivada de uma curva pode ser determinada a qualquer momento. O valor máximo/mínimo pode, portanto, ser determinado definindo esses valores iguais a 0 e, em seguida, determinando os valores correspondentes. dy/dx = 0, 2ax+b = 0, x = -b/2a

3. Substitua este valor de x em y para o valor mínimo/máximo.
Método 4 de 4: Exemplos

1. Determine o valor máximo ou mínimo da função f(x) = x + x + 1.

2. Determine o valor máximo ou mínimo da função f(x) = -2(x-1) + 3.
Pontas
- O eixo de simetria da parábola é x = h.
- -h é o valor correspondente ao valor máximo ou mínimo.
Artigos sobre o tópico "Determinando os valores máximo e mínimo de uma função quadrática"
Оцените, пожалуйста статью
Popular