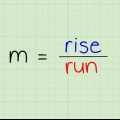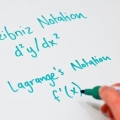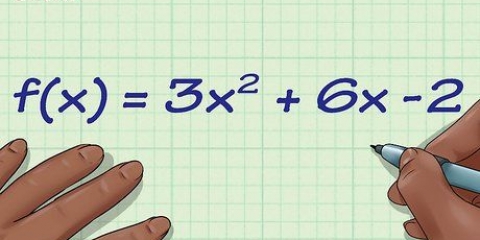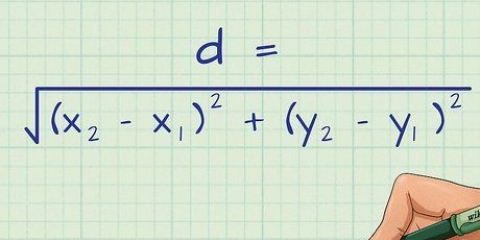Inclinação = 2 
Inclinação = -1 
inclinação = 

Encontre a inclinação de 
Converta para o formulário  :
: 



Determine a inclinação: Inclinação = M = 4 

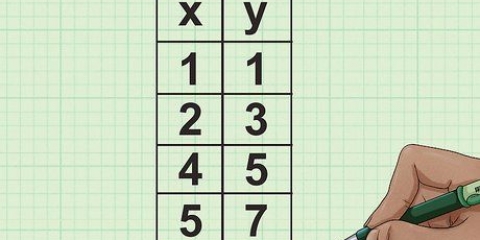
Em cada par, a coordenada x é o primeiro número e a coordenada y é o segundo número após o ponto decimal. Cada coordenada x em uma linha tem uma coordenada y correspondente. 
X1: 2 y1: 4 X2: 6 y2: 6 
Pontos originais: (2.4) e (6.6). Aplique à fórmula ponto-inclinação: 
Simplifique para a resposta final:  = inclinação
= inclinação



Com este método, faça a si mesmo a seguinte pergunta: "Qual é a inclinação da linha  no ponto (4.2)?"
no ponto (4.2)?" A derivada geralmente é escrita como ![Determinando a inclinação de uma linha f`src=]() ou
ou 
4 X + 6 

Determinando a inclinação de uma linha
Contente
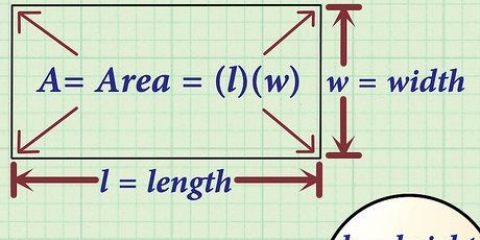
A inclinação de uma linha é uma medida de quão rápido a linha muda. Isso pode ser feito com uma linha reta - onde a inclinação informa exatamente o quanto para cima (inclinação positiva) ou para baixo (inclinação negativa) uma linha percorre uma certa distância. A inclinação também pode ser usada para uma tangente a uma curva. Ou pode ser uma linha curva, usada em análise, onde a inclinação também é conhecida como a `derivada` de uma função. De qualquer forma, pense na inclinação como a "taxa de variação" de um gráfico: se a variável "x" aumenta, a que taxa "y" varia?? Essa é uma maneira de pensar a inclinação como causa e efeito.
Degraus
Método 1 de 3: Encontrando a inclinação de uma equação linear

1. Use a inclinação para determinar quão íngreme e em qual direção (para cima ou para baixo) uma linha vai. Determinar a inclinação de uma linha é fácil, desde que você tenha ou possa elaborar uma equação linear. Este método só funciona quando:
- As variáveis não têm expoentes.
- Existem apenas duas variáveis, e nenhuma delas são frações (por exemplo, o seguinte não pode ser:
)
- A equação pode ser simplificada para a forma
, através do qual m e b constantes (números como 3, 10, -12,
).
2. Encontre o número antes do x, geralmente escrito como `m` para determinar a inclinação. Se a equação já estiver na forma correta,  , em seguida, basta escolher o número na posição `m` (mas se não houver número antes de x, a inclinação é 1). Então essa também é a inclinação! Saiba que este número, m, é sempre multiplicado pela variável, neste caso um `x`. Confira os exemplos a seguir:
, em seguida, basta escolher o número na posição `m` (mas se não houver número antes de x, a inclinação é 1). Então essa também é a inclinação! Saiba que este número, m, é sempre multiplicado pela variável, neste caso um `x`. Confira os exemplos a seguir:
 , em seguida, basta escolher o número na posição `m` (mas se não houver número antes de x, a inclinação é 1). Então essa também é a inclinação! Saiba que este número, m, é sempre multiplicado pela variável, neste caso um `x`. Confira os exemplos a seguir:
, em seguida, basta escolher o número na posição `m` (mas se não houver número antes de x, a inclinação é 1). Então essa também é a inclinação! Saiba que este número, m, é sempre multiplicado pela variável, neste caso um `x`. Confira os exemplos a seguir:




3. Reconhecer a equação onde uma variável é isolada se a inclinação não for clara. Você pode adicionar, subtrair, multiplicar, etc. para isolar uma variável (geralmente o `y`). Lembre-se de que tudo o que você fizer em um lado do sinal de igual (como adicionar 3), você deve fazer isso do outro lado também. Seu objetivo final é uma equação, como  . Por exemplo:
. Por exemplo:
 . Por exemplo:
. Por exemplo:
 :
:



Método 2 de 3: Determinando a inclinação com dois pontos

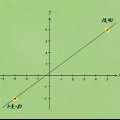
1. Use um gráfico e dois pontos para encontrar rapidamente a inclinação sem a equação. Se você tiver um gráfico e uma linha, mas nenhuma equação, ainda poderá determinar a inclinação com facilidade. Tudo que você precisa são dois pontos na linha, que você aplica à equação  . Ao determinar a inclinação, tenha em mente as seguintes informações para se certificar de que está no caminho certo:
. Ao determinar a inclinação, tenha em mente as seguintes informações para se certificar de que está no caminho certo:
 . Ao determinar a inclinação, tenha em mente as seguintes informações para se certificar de que está no caminho certo:
. Ao determinar a inclinação, tenha em mente as seguintes informações para se certificar de que está no caminho certo: - As inclinações positivas sobem e para a direita.
- As inclinações negativas vão para baixo e para a direita.
- Encostas mais íngremes são linhas mais íngremes. As encostas menos íngremes são sempre mais graduais.
- Linhas horizontais perfeitas têm uma inclinação de zero.
- Linhas perfeitamente verticais não têm inclinação alguma. Sua inclinação (ou inclinação) é `indefinida`.

2. Escolha dois pontos, colocando-os na forma simples (x, y). Use o gráfico (ou pergunta de atribuição) para encontrar as coordenadas xey de dois pontos no gráfico. Eles podem consistir em quaisquer dois pontos pelos quais a linha passa. Por exemplo, suponha que neste método a linha passe pelo ponto (2.4) e por (6.6).

3. Rotule os pontos x1, y1, X2, y2, e manter cada ponto com seu par. Continuando com nosso primeiro exemplo, usando os pontos (2.4) e (6.6), rotule as coordenadas xey de cada ponto. Se tudo correu bem, agora você acaba com:

4. Substitua esses pontos na `fórmula ponto-inclinação` para encontrar a inclinação. A seguinte fórmula é usada para determinar a inclinação usando quaisquer dois pontos em uma linha reta:  . Basta substituir os quatro pontos e simplificar:
. Basta substituir os quatro pontos e simplificar:
 . Basta substituir os quatro pontos e simplificar:
. Basta substituir os quatro pontos e simplificar:
 = inclinação
= inclinação
5. Entenda como funciona a fórmula ponto-inclinação. A inclinação de uma linha é indicada pela mudança de y de x (y/x): quanto a linha sobe dividido por quanto a linha continua para a direita. O aumento da linha é a diferença entre os valores de y (lembre-se, o eixo y sobe e desce), e o aumento da linha é a diferença entre os valores de x (e o eixo x vai de esquerda para direita).

6. Aprenda outras maneiras que você precisa saber para determinar a inclinação. A equação da inclinação é  . Isso também pode ser representado pela letra grega `Δ` (`delta`), que significa `diferença`. A inclinação também pode ser representada como Δy/Δx, significando `diferença de y` / `diferença de x`. Esta é exatamente a mesma pergunta que "Determine a inclinação entre…"
. Isso também pode ser representado pela letra grega `Δ` (`delta`), que significa `diferença`. A inclinação também pode ser representada como Δy/Δx, significando `diferença de y` / `diferença de x`. Esta é exatamente a mesma pergunta que "Determine a inclinação entre…"
 . Isso também pode ser representado pela letra grega `Δ` (`delta`), que significa `diferença`. A inclinação também pode ser representada como Δy/Δx, significando `diferença de y` / `diferença de x`. Esta é exatamente a mesma pergunta que "Determine a inclinação entre…"
. Isso também pode ser representado pela letra grega `Δ` (`delta`), que significa `diferença`. A inclinação também pode ser representada como Δy/Δx, significando `diferença de y` / `diferença de x`. Esta é exatamente a mesma pergunta que "Determine a inclinação entre…"Método 3 de 3: Use o cálculo diferencial para encontrar a inclinação de uma curva

1. Revise como você pode determinar a derivada de funções comuns de diferentes maneiras. As derivadas fornecem a taxa de variação (ou inclinação) em um ponto de uma linha. A linha pode ser curva ou reta – não importa. Lembre-se de como a linha muda a qualquer momento, em vez de como a inclinação de toda a linha muda. Como você determina a derivada depende do tipo de função, então revise como determinar a derivada de funções antes de continuar.
- Leia aqui sobre como determinar a derivada
- As derivadas mais simples, aquelas para equações exponenciais padrão, você pode encontrar facilmente com um método rápido. Você usará isso no resto do método.

2. Entenda quais problemas exigem que você calcule a inclinação usando derivadas. Você nem sempre será solicitado explicitamente pela derivada ou inclinação de uma curva. Você também pode ser questionado sobre a `taxa de variação` no ponto (x, y). Você pode ser solicitado a fornecer uma equação para a inclinação do gráfico, o que significa simplesmente encontrar a derivada. Finalmente, você pode ser solicitado a `a inclinação da linha tangente em (x, y)`. Isso significa novamente que ele só pede a inclinação da curva em um ponto específico (x, y).
 no ponto (4.2)?"
no ponto (4.2)?"
3.Encontre a derivada da função. Você nem precisa de um gráfico real, apenas a função ou equação do gráfico. Neste exemplo, usamos uma função discutida anteriormente,


4.Substitua o ponto na equação da derivada para encontrar a inclinação. A diferencial de uma função fornece a inclinação da função em um determinado ponto. Em outras palavras, f"(x) é a inclinação da função a qualquer momento (x,f(x)). Então, para este problema de exercício:
Artigos sobre o tópico "Determinando a inclinação de uma linha"
Оцените, пожалуйста статью
Similar
Popular