Instruções gratuitas passo a passo 
Se o coeficiente (inclinação) uma na equação é positivo, a parábola abre para cima (em uma parábola orientada verticalmente), se a letra maiúscula é `U` e o vértice é um mínimo. Enquanto o uma negativo, a parábola abre para baixo e o vértice tem um máximo. Se você está tendo problemas para se lembrar disso, pense assim: uma equação com um positivo a parece um sorriso; uma comparação com um negativo a parece uma carranca. Digamos que você tenha a seguinte equação: y = 2x -1. Esta parábola tem a forma de um `U` porque o uma (2) é positivo. Se a equação tiver um termo y em vez de um termo x na segunda potência, então a parábola será orientada horizontalmente e aberta lateralmente (para a direita ou esquerda), como um `C` ou um `C` invertido. Por exemplo: a parábola y = x + 3 abre para a direita, como um `C`. 
No exemplo acima (y = 2x² -1), . é a = 2 e b = 0`.` Agora você pode calcular o eixo de simetria preenchendo os números:x = -0 / (2)(2) = 0`.` Neste caso, o eixo de simetria é x = 0 (ou seja, o eixo y do sistema de coordenadas). 
As coordenadas do vértice também são chamadas (h, k). Nesse caso h igual a 0 e k igual a -1. A equação da parábola pode ser escrita na forma y = a(x - h)² + k. Nesta forma, o vértice é o ponto (h, k) e você não precisa fazer nenhum cálculo para encontrar o vértice além da interpretação correta do gráfico. 
O valor médio de x deve ser o eixo de simetria no caso de uma parábola `vertical`. Você deve incluir pelo menos dois valores acima e abaixo do valor médio para x na tabela de simetria. Neste exemplo você coloca o valor do eixo de simetria (x = 0) no meio da tabela. 
E se x = -2, então y: y = (2) (-2) - 1 = 8 - 1 = 7 E se x = -1, então y: y = (2) (-1) - 1 = 2 - 1 = 1 E se x = 0, então y: y = (2) (0) - 1 = 0 - 1 = -1 E se x = 1, então y: y = (2) (1) - 1 = 2 - 1 = 1 E se x = 2, então y: y = (2) (2) - 1 = 8 - 1 = 7 
O eixo x é horizontal, o eixo y é vertical. Os números positivos no eixo y estão acima e os números negativos abaixo do ponto (0, 0). Os números positivos no eixo x estão à direita e os números negativos à esquerda do ponto (0, 0). 
Desenhe uma parábola
Contente
Uma parábola é uma curva bidimensional simétrica que tem a forma de um arco. Cada ponto da parábola é equidistante de um ponto fixo (o foco) e de uma linha reta fixa (a diretriz). Para mapear uma parábola, você precisa encontrar o topo da parábola, bem como alguns pontos de cada lado dela, para marcar o caminho que os pontos percorrem.
Degraus
Parte 1 de 2: Desenhando uma parábola
1. Entenda as partes de uma parábola. Você pode receber algumas informações antes de começar, e conhecer a terminologia o ajudará a evitar etapas desnecessárias. Aqui estão as partes da parábola que você precisa conhecer:
- O foco. Um ponto fixo no interior da parábola que é usado para a definição formal da curva.
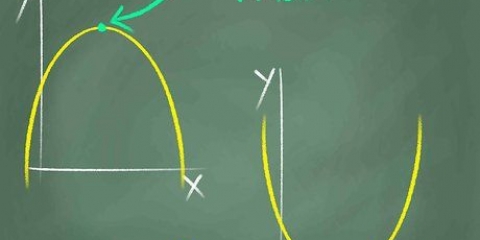
- o diretor. Uma linha sólida e reta. A parábola é o lugar geométrico ou conjunto de pontos em que um dado ponto é equidistante do foco e a diretriz está localizado. (Veja gráfico acima.)
- O eixo de simetria. Esta é uma linha reta passando pelo vértice da parábola e equidistante dos pontos correspondentes nos dois braços da parábola.
- o vértice. O ponto onde o eixo de simetria intercepta a parábola é chamado de vértice da parábola. Se a parábola abre para cima ou para a direita, o vértice é um mínimo da curva. Se a parábola abre para baixo ou para a esquerda, o vértice é um máximo.
2. Conheça a equação de uma parábola. A equação geral de uma parábola é y = ax+bx+c. Também pode ser escrito na forma ainda mais geral y = a(x – h)² + k, mas vamos nos concentrar aqui na primeira forma da equação.
3. Encontre o eixo de simetria. Lembre-se que o eixo de simetria é a reta que passa pelo ponto de virada (vértice) da parábola. No caso de uma parábola vertical (vale ou montanha), o eixo é o mesmo que a coordenada x do vértice, ou seja, o valor x do ponto onde o eixo de simetria intercepta a parábola. Use esta fórmula para encontrar o eixo de simetria: x = -b/2a.
4. Encontre o vértice. Depois de conhecer o eixo de simetria, você pode inserir esse valor em x para obter a coordenada y. Estas duas coordenadas dão-lhe o vértice da parábola. Neste caso, você substitui 0 em 2x -1 para obter a coordenada y. y = 2 x 0 -1 = 0 -1 = -1. O vértice é (0,-1) e a parábola intercepta o eixo y em -1.
5. Crie uma tabela de valores para x. Crie uma tabela com determinados valores para x na primeira coluna. Esta tabela fornece as coordenadas necessárias para representar graficamente a equação.
6. Calcule os valores das coordenadas y correspondentes. Substitua qualquer valor de x na equação da parábola e calcule os valores correspondentes de y. Coloque esses valores calculados de y na tabela. Neste exemplo, os valores de y são calculados da seguinte forma:
7. Insira os valores calculados de y na tabela. Agora você encontrou pelo menos cinco pares de coordenadas para a parábola e está quase pronto para desenhar a parábola. Com base no seu trabalho, agora você tem os seguintes pontos: (-2, 7), (-1, 1), (0, -1), (1, 1), (2, 7). Lembre-se que a parábola (simétrica) é representada em relação ao eixo de simetria. Isso significa que as coordenadas y dos pontos diretamente opostos um ao outro em relação ao eixo de simetria serão iguais. As coordenadas y associadas às coordenadas x -2 e +2 são ambas 7; as coordenadas y pertencentes às coordenadas x -1 e +1 são ambas 1, e assim por diante.
8. Desenhe os pontos da tabela no sistema de coordenadas. Cada linha da tabela forma um par de coordenadas (x, y) no sistema de coordenadas. Desenhe todos os pontos usando as coordenadas na tabela.
9. Ligue os pontos. Para representar graficamente a parábola, conecte os pontos desenhados na etapa anterior. O gráfico neste exemplo se parece com um U. Conecte os pontos usando linhas ligeiramente curvas (em vez de retas). Isso cria a imagem mais precisa da parábola (que é ligeiramente curvada em todo o seu comprimento). Em cada extremidade da parábola, você pode desenhar setas apontando para fora do vértice, se quiser. Isso indica que a parábola continua indefinidamente.
Parte 2 de 2: Deslocando o gráfico de uma parábola
Se você quer uma maneira mais rápida de deslocar uma parábola sem ter que reencontrar seu vértice e reespecificar diferentes pontos na parábola, então você precisa entender a equação de uma parábola e aprender a convertê-la verticalmente ou horizontalmente. Comece com a parábola básica: y = x. Tem um vértice no ponto (0, 0) e é uma parábola de vale. Alguns pontos do gráfico são: (-1, 1), (1, 1), (-2, 4) e (2, 4). Você pode deslocar uma parábola com base na equação.
1. Mover uma parábola para cima. Considere a equação y = x +1. Isso desloca a parábola original em uma unidade. O vértice agora é (0, 1) em vez de (0, 0). Sua forma não mudou, mas cada coordenada y será deslocada uma unidade para cima. Então, em vez de (-1, 1) e (1, 1), desenhamos os pontos (-1, 2) e (1, 2).
2. Mover uma parábola para baixo. Pegue a equação y = x-1. Deslocamos a parábola original em uma unidade para que o vértice seja agora (0, -1) em vez de (0, 0,). Ela ainda terá a mesma forma da parábola original, mas cada coordenada y será deslocada uma unidade para baixo. Então, em vez de (-1, 1) e (1, 1), por exemplo, desenhamos (-1, 0) e (1, 0).
3. Mover uma parábola para a esquerda. Considere a equação y = (x + 1). Isso desloca a parábola original uma unidade para a esquerda. O vértice agora é (-1, 0) em vez de (0, 0). A forma da parábola original permanece a mesma, mas cada coordenada x é deslocada uma para a esquerda. Por exemplo, em vez de (-1, 1) e (1, 1), desenhamos (-2, 1) e (0, 1).
4. Mover uma parábola para a direita. Considere a equação y = (x - 1). Esta é a parábola original deslocada uma unidade para a direita. O vértice agora é (1, 0) em vez de (0, 0). A forma da parábola original permanece a mesma, mas cada coordenada x é deslocada uma posição para a direita. Por exemplo, em vez de (-1, 1) e (1, 1), desenhamos (0, 1) e (2, 1).
Artigos sobre o tópico "Desenhe uma parábola"
Оцените, пожалуйста статью
Similar
Popular
