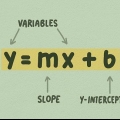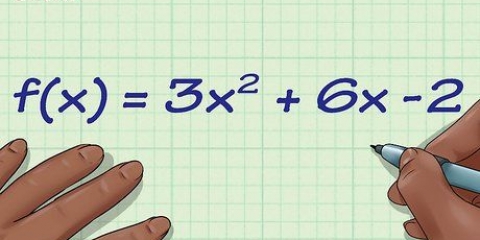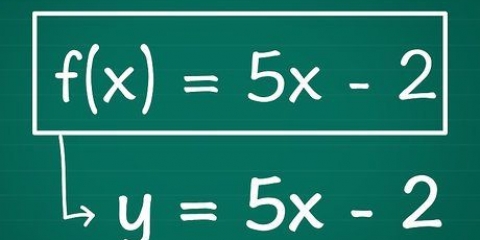Se a inclinação for negativa, significa que a linha desce quando você vai para a direita. 





-1: -1 + 2 = 1 0: 0 +2 = 2 1: 1 + 2 = 3 




Faça F(x) igual a zero:
Resolver:




Algumas funções quadráticas, como  nunca são negativos. Então existe uma assíntota em 0.
nunca são negativos. Então existe uma assíntota em 0. A menos que você esteja trabalhando com números imaginários, isso não é possível: 
Equações com expoentes complexos podem ter muitas assíntotas. 
Para a comparação  , você poderia preencher -1, 0, 1, -2, 2, -10 e 10. Isso lhe dá um bom intervalo de números para comparar.
, você poderia preencher -1, 0, 1, -2, 2, -10 e 10. Isso lhe dá um bom intervalo de números para comparar. Seja inteligente ao selecionar números. No exemplo, você percebe rapidamente que um sinal negativo não importa -- por exemplo, você pode parar de testar -10, porque será o mesmo que 10. 
Assuma de dois a quatro valores grandes para x, meio negativo e meio positivo, e desenhe os pontos. O que acontece se você inserir `infinito` para uma variável? A função se torna infinitamente maior ou menor? Se os graus são iguais em uma fração, como  , depois é só dividir os dois primeiros coeficientes (
, depois é só dividir os dois primeiros coeficientes ( para obter sua assíntota final (-0,5).
para obter sua assíntota final (-0,5). Se os graus em uma fração forem diferentes, divida a equação no numerador pela equação no denominador usando a divisão polinomial longa. 

Desenhando o gráfico de uma função
Contente
Um gráfico de uma função é uma representação visual do comportamento de uma função em um plano x-y. Os gráficos nos ajudam a entender vários aspectos da função que seriam difíceis de entender apenas olhando para a própria função. Você pode representar graficamente milhares de equações, e existem fórmulas diferentes para cada equação. No entanto, sempre há maneiras de representar graficamente uma função se você esqueceu as etapas exatas para o tipo específico de função.
Degraus
Método 1 de 3: Faça um gráfico de uma equação linear com uma tangente

1. Saiba que funções lineares são linhas simples e fáceis de desenhar, como y = 2 X + 5  . Há uma variável e uma constante, escritas como
. Há uma variável e uma constante, escritas como  em uma função linear, sem expoentes, radicais, etc. Se você tem uma equação tão simples, o gráfico da função também é simples. Outros exemplos de funções lineares são:
em uma função linear, sem expoentes, radicais, etc. Se você tem uma equação tão simples, o gráfico da função também é simples. Outros exemplos de funções lineares são:
 . Há uma variável e uma constante, escritas como
. Há uma variável e uma constante, escritas como  em uma função linear, sem expoentes, radicais, etc. Se você tem uma equação tão simples, o gráfico da função também é simples. Outros exemplos de funções lineares são:
em uma função linear, sem expoentes, radicais, etc. Se você tem uma equação tão simples, o gráfico da função também é simples. Outros exemplos de funções lineares são: 
2. Use a constante para indicar a interseção com o eixo y. A interseção com o eixo y é o ponto onde a função cruza o eixo y em seu gráfico. Em outras palavras, é o ponto em que  . Então, para encontrá-lo, basta definir x para zero e deixar a constante na equação. No exemplo anterior,
. Então, para encontrá-lo, basta definir x para zero e deixar a constante na equação. No exemplo anterior,  , é a interseção com o eixo y igual a y = 5, ou seja, o ponto (0,5). Marque este ponto em seu gráfico com um ponto.
, é a interseção com o eixo y igual a y = 5, ou seja, o ponto (0,5). Marque este ponto em seu gráfico com um ponto.
 . Então, para encontrá-lo, basta definir x para zero e deixar a constante na equação. No exemplo anterior,
. Então, para encontrá-lo, basta definir x para zero e deixar a constante na equação. No exemplo anterior,  , é a interseção com o eixo y igual a y = 5, ou seja, o ponto (0,5). Marque este ponto em seu gráfico com um ponto.
, é a interseção com o eixo y igual a y = 5, ou seja, o ponto (0,5). Marque este ponto em seu gráfico com um ponto.
3. Encontre a inclinação da sua linha com o número imediatamente antes da variável. No exemplo,  , é a inclinação `2`. Isso porque 2 pertence à variável `x`. A inclinação indica quão íngreme é uma linha, ou quão alto a linha vai antes de virar à direita ou à esquerda. Uma inclinação maior significa uma linha mais íngreme.
, é a inclinação `2`. Isso porque 2 pertence à variável `x`. A inclinação indica quão íngreme é uma linha, ou quão alto a linha vai antes de virar à direita ou à esquerda. Uma inclinação maior significa uma linha mais íngreme.
 , é a inclinação `2`. Isso porque 2 pertence à variável `x`. A inclinação indica quão íngreme é uma linha, ou quão alto a linha vai antes de virar à direita ou à esquerda. Uma inclinação maior significa uma linha mais íngreme.
, é a inclinação `2`. Isso porque 2 pertence à variável `x`. A inclinação indica quão íngreme é uma linha, ou quão alto a linha vai antes de virar à direita ou à esquerda. Uma inclinação maior significa uma linha mais íngreme.
4. Faça uma fração da inclinação. A inclinação tem a ver com a inclinação, e a inclinação é simplesmente a diferença entre o movimento para cima e para baixo, e para a esquerda e para a direita. A inclinação é uma fração de a variação de y em comparação com a variação de x. Quanto deve a linha `mudar em y` antes de `mudar em x`? No exemplo, a inclinação `2` pode ser lida como  .
.
 .
.
5. Comece em sua interseção com o eixo y e siga as mudanças em y e x, para desenhar mais pontos. Depois de conhecer a inclinação, use-a para desenhar sua função linear. Comece na interseção com o eixo y, aqui (0,5), depois suba 2 e à direita 1. Marque também este ponto (1,7). Encontre outros 1-2 pontos para desenhar o gráfico.

6. Use uma régua para conectar seus pontos e representar graficamente sua função linear. Para evitar erros ou gráficos grosseiros, encontre e conecte pelo menos três pontos separados, embora dois sejam suficientes em uma emergência. Este é o gráfico da sua equação linear!
Método 2 de 3: Estimando pontos em um gráfico

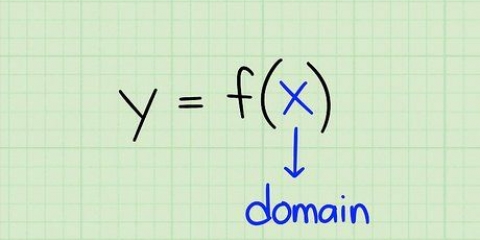
1. Determine a função. Tome a função da forma f(X), verdadeiro y representa o intervalo, X representa o domínio e f a função. Como exemplo usamos y = x+2, através do qual f(X) = x+2.

2. Desenhe duas linhas cruzadas em uma folha de papel. A linha horizontal é você X-cinzas. A linha vertical é você y-cinzas.

3. Numere seu gráfico. Destaque tanto o X-como se o y-eixo com números equidistantes um do outro. Para o X-eixo são os números positivos à direita e negativos à esquerda. Para o y-eixo são os números positivos na parte superior e negativos na parte inferior.

4. Calcular um y-valor para 2-3 X-valores. Assuma a função f(X) = x+2. Calcule alguns valores para y pelos valores correspondentes para X visível no eixo na função. Para equações mais complicadas, pode ser necessário simplificar a função, isolando uma variável primeiro.

5. Desenhe o ponto do gráfico para cada par. Desenhe linhas verticais finas imaginárias ao longo do X-eixo e horizontalmente ao longo do y-cinzas. O ponto onde essas linhas se cruzam é um ponto gráfico (ou apenas use papel quadriculado).

6. Remova as linhas imaginárias. Depois de desenhar todos os pontos do gráfico, você pode apagar as linhas imaginárias. Nota: o gráfico de f(x) = x seria uma linha paralela a ele através da origem (0,0), mas f(x) = x+2 é deslocado duas unidades (ao longo do eixo y) na grade por causa do +2 na equação.
Método 3 de 3: Representando graficamente uma função complexa

1. Entenda como representar graficamente tipos comuns de equações. Existem tantas estratégias de gráficos diferentes quanto tipos de funções, muitas para cobrir completamente aqui. Se você achar isso difícil e uma estimativa não funcionar, confira os artigos sobre:
- Funções quadráticas
- Funções Racionais
- Funções logarítmicas
- Desigualdades (sem características, mas informações úteis, no entanto).

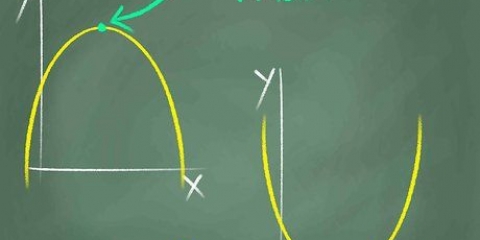
2.Primeiro determine os zeros. Zeros são os pontos onde o gráfico intercepta a linha horizontal no gráfico. Embora nem todos os gráficos tenham zeros, a maioria tem, e é o primeiro passo que você precisa dar para acertar tudo. Para encontrar zeros, primeiro defina toda a função como zero e, em seguida, resolva-a. Por exemplo:







3. Encontre e marque quaisquer assíntotas horizontais (lugares onde a função é impossível de alcançar) com uma linha pontilhada. Geralmente são pontos onde o gráfico não existe, como onde você divide por zero. Se sua equação tem uma variável em uma fração, como  , então comece zerando o fundo da fração. Você pode mapear todos os lugares onde é igual a zero (neste exemplo uma linha pontilhada em x=2 e x=-2), porque você nunca pode dividir por zero. No entanto, frações não são os únicos lugares para encontrar assíntotas. Normalmente, tudo o que você precisa é de algum bom senso:
, então comece zerando o fundo da fração. Você pode mapear todos os lugares onde é igual a zero (neste exemplo uma linha pontilhada em x=2 e x=-2), porque você nunca pode dividir por zero. No entanto, frações não são os únicos lugares para encontrar assíntotas. Normalmente, tudo o que você precisa é de algum bom senso:
 , então comece zerando o fundo da fração. Você pode mapear todos os lugares onde é igual a zero (neste exemplo uma linha pontilhada em x=2 e x=-2), porque você nunca pode dividir por zero. No entanto, frações não são os únicos lugares para encontrar assíntotas. Normalmente, tudo o que você precisa é de algum bom senso:
, então comece zerando o fundo da fração. Você pode mapear todos os lugares onde é igual a zero (neste exemplo uma linha pontilhada em x=2 e x=-2), porque você nunca pode dividir por zero. No entanto, frações não são os únicos lugares para encontrar assíntotas. Normalmente, tudo o que você precisa é de algum bom senso: nunca são negativos. Então existe uma assíntota em 0.
nunca são negativos. Então existe uma assíntota em 0.

4. Aplique os valores e desenhe diferentes pontos. Basta escolher alguns valores para x e resolver para a função. Em seguida, faça um gráfico dos pontos em seu gráfico. Quanto mais complicado o gráfico, mais pontos você precisa. Em geral, -1, 0 e 1 são os pontos mais fáceis de obter, embora você queira ter mais dois ou três em cada lado do zero para obter um bom gráfico.
 , você poderia preencher -1, 0, 1, -2, 2, -10 e 10. Isso lhe dá um bom intervalo de números para comparar.
, você poderia preencher -1, 0, 1, -2, 2, -10 e 10. Isso lhe dá um bom intervalo de números para comparar.
5. Mapeie o comportamento final da função para ver o que acontece quando ela fica realmente grande. Isso lhe dá uma ideia da direção geral de uma função, geralmente como um vertical assíntota. Por exemplo: você sabe que  eventualmente se torna muito, muito grande. Apenas um `x` extra (um milhão versus um milhão e um) torna y muito maior. Existem algumas maneiras de testar o comportamento final, incluindo:
eventualmente se torna muito, muito grande. Apenas um `x` extra (um milhão versus um milhão e um) torna y muito maior. Existem algumas maneiras de testar o comportamento final, incluindo:
 eventualmente se torna muito, muito grande. Apenas um `x` extra (um milhão versus um milhão e um) torna y muito maior. Existem algumas maneiras de testar o comportamento final, incluindo:
eventualmente se torna muito, muito grande. Apenas um `x` extra (um milhão versus um milhão e um) torna y muito maior. Existem algumas maneiras de testar o comportamento final, incluindo: , depois é só dividir os dois primeiros coeficientes (
, depois é só dividir os dois primeiros coeficientes ( para obter sua assíntota final (-0,5).
para obter sua assíntota final (-0,5).
6. Conecte os pontos, evitando o comportamento assintótico e final, para estimar o gráfico. Depois de ter cinco ou seis pontos, as assíntotas e uma ideia geral do comportamento final, use tudo isso para construir uma versão aproximada do gráfico.

7. Dê gráficos perfeitos usando uma calculadora gráfica. As calculadoras gráficas são computadores portáteis poderosos que podem fornecer gráficos exatos para qualquer equação. Eles permitem que você localize pontos exatos, encontre linhas de inclinação e visualize equações difíceis com facilidade. Basta digitar a equação exata na seção do gráfico (geralmente um botão rotulado `F(x) = `) e pressionar o botão do gráfico para ter uma ideia da função.
Pontas
- Calculadoras gráficas são uma ótima maneira de praticar. Tente fazer um gráfico à mão e, em seguida, use a calculadora para obter uma imagem perfeita do gráfico e compare os dois gráficos.
- Se você realmente não sabe mais o que fazer, basta inserir alguns pontos. Basicamente você poderia desenhar a função inteira assim, se você tentasse um número infinito de combinações de números.
Artigos sobre o tópico "Desenhando o gráfico de uma função"
Оцените, пожалуйста статью
Similar
Popular