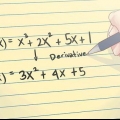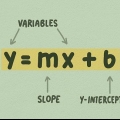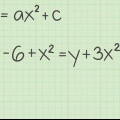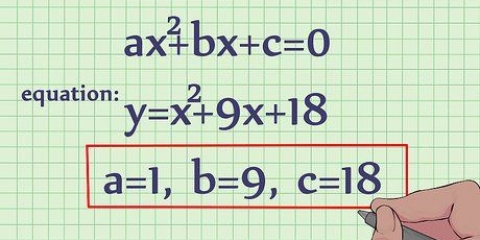Um ponto e uma inclinação são dados. Dois pontos são dados, mas nenhuma inclinação. Dado um ponto e outra reta paralela a ele. Dado um ponto e outra reta perpendicular a ele. 




Reorganize sua equação. b = y - mx. Insira os valores e resolva. b = -5 - (2/3)6. b = -5 - 4. b = -9 Verifique se a interseção com o eixo y é realmente -9. Escreva a equação: y = 2/3 x - 9 

Use sua inclinação e coordenadas na equação acima. Multiplique a inclinação (m) com a coordenada x do ponto. Subtraia o valor da coordenada y do ponto. você agora tem b resolvido, a interseção com o eixo y. 



Calcule a inclinação. A inclinação = (Y2 - S1) / (X2 - X1) -12 - (-5) / 8 - 6 = -7 / 2 A inclinação é -7/2 (do primeiro ponto ao segundo vamos 7 para baixo e 2 para a direita, então a inclinação é -7 sobre 2). Reorganize sua equação. b = y - mx. Insira os valores e resolva. b = -12 - (-7/2)8. b = -12 - (-28). b = -12 + 28. b = 16 Observação: como usamos o 8 para as coordenadas, também devemos usar o -12.Se você usar o 6 para suas coordenadas, você também deve usar o -5. Verifique se sua interseção com o eixo y é realmente 16. Escreva a equação: y = -7/2 x + 16 
Substitua a inclinação e as coordenadas na equação acima. Multiplique a inclinação (m) com a coordenada x do ponto. Subtraia o valor da coordenada y do ponto. Você tem b resolvido, a interseção com o eixo y. 


Resolva a inclinação. A inclinação da nossa nova linha será igual à inclinação da linha antiga. Determine a inclinação da linha antiga: -2a = -5x + 1 puxar "-2" fora de ambos os lados: y = 5/2x - 1/2 A inclinação é 5/2. Reorganize sua equação. b = y - mx. Preencha e resolva. b = 3 - (5/2)4. b = 3 - (10). b = -7. Verifique se a interseção com o eixo y é realmente -7. Escreva a equação: y = 5/2 x - 7 
2/3 torna-se -3/2 -6/5 torna-se 5/6 3 (ou 3/1 — é o mesmo) torna-se -1/3 -1/2 se torna 2 
Conecte sua inclinação e coordenadas na equação acima. Multiplique a inclinação (m) com a coordenada x do ponto. Subtraia esse valor da coordenada y do ponto. Agora você resolveu a equação para b; a interseção com o eixo y. 


Resolva a inclinação. A inclinação da nossa nova linha torna-se o inverso negativo da inclinação da linha antiga. Determine a inclinação da linha antiga: 2a = -4x + 9 puxar "2" fora de ambos os lados: y = -4/2x + 9/2 A inclinação é -4/2 ou -2. O recíproco negativo de -2 é 1/2. reorganize sua equação. b = y - mx. Preencha e resolva. b = -1 - (1/2)8. b = -1 - (4). b = -5. Verifique se sua interseção com o eixo y é realmente -5. Escreva a equação: y = 1/2 x - 5
Encontrando a equação de uma reta
Contente
Para encontrar a equação de uma reta você tem preciso de duas coisas:a) um ponto na linha; e b) a inclinação (às vezes também a inclinação) da linha. Mas como você coleta essas duas informações e o que você faz com elas depois pode ser muito diferente dependendo da situação. Por uma questão de simplicidade, este artigo se concentrará em equações da forma y = mx + b em vez de (s-s1) = m(x - x1).
Degraus
Método 1 de 5: Informações Gerais
1. Saiba o que procurar.Antes de procurar a comparação, você precisa saber com certeza o que está tentando encontrar. Tenha em mente o seguinte:
- Os pontos são classificados como par ordenado, como (-7, -8) ou (-2,-6).
- O primeiro número de um par ordenado é o coordenada x. Esta é a posição horizontal do ponto (quantas unidades à esquerda ou à direita da origem).
- O segundo número em um par ordenado é o coordenada y. Esta é a posição vertical do ponto (quantas unidades acima ou abaixo da origem).
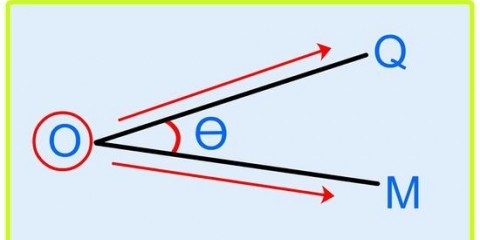
- O declive entre os dois pontos é chamado de "a inclinação" — em outras palavras, quão longe você tem que subir (ou descer) e direita (ou esquerda) para ir de um ponto a outro.
- Duas linhas são paralelo se eles não se cruzam.
- Duas linhas são perpendiculares entre si se eles se cruzam em um ângulo reto (90 graus).
2. Determine com que tipo de tarefa você está lidando.
3. Resolva o problema usando um dos quatro métodos abaixo. Dependendo das informações fornecidas, existem diferentes maneiras de resolvê-lo.
Método 2 de 5: Um ponto e uma inclinação são dados

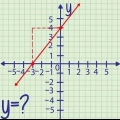
1. Encontre a interseção de sua equação com o eixo y. A interseção com o eixo y (ou a variável b em nossa equação) é o ponto em que a linha cruza com o eixo y. Você pode calcular a interseção com o eixo y reorganizando a equação para resolver b. Nossa nova equação agora se parece com isso: b = y - mx.
- Digite sua inclinação e coordenadas na equação acima.
- Multiplique a inclinação (m) com a coordenada x do ponto.
- Subtraia esse valor da coordenada y do ponto.
- Agora você tem b resolvido, a interseção com o eixo y.

2. Escreva a fórmula:y = ____ x + ____ , juntamente com os espaços em branco.

3. Preencha o primeiro espaço vazio, o do x, com a inclinação.

4. Preencha o segundo espaço em branco com a interseção com o eixo y que você calculou antes.

5. Resolva o problema do exemplo. "Dado o ponto (6, -5) e a inclinação 2/3, qual é a equação da reta?"
Método 3 de 5: Dois pontos são dados
1. Calcule a inclinação entre dois pontos. A inclinação também é chamada de declive e você pode pensar nisso como a taxa na qual algo se move ao longo de um eixo imaginário y e eixo x. A equação para a inclinação é: (Y2 - S1) / (X2 - X1)
- Pegue os dois pontos e use-os na equação (duas coordenadas significam duas y-valores e dois X-valores). Não importa quais coordenadas você insira primeiro, desde que você faça isso de forma consistente. Alguns exemplos:
- Pontos (3, 8) e (7, 12). (S2 - S1) / (X2 - X1) = 12 - 8 / 7 - 3 = 4/4, ou 1.
- Pontos (5, 5) e (9, 2). (S2 - S1) / (X2 - X1) = 2 - 5 / 9 - 5 = -3/4.

2. Escolha um conjunto de coordenadas para o resto do problema. Risque ou cubra o outro conjunto de coordenadas para não usá-los acidentalmente.

3. Calcule a interseção com o eixo y da sua equação. Novamente, reorganize a fórmula y = mx + b para obter uma equação da forma b = y – mx. Ainda é a mesma equação; você acabou de reorganizar.

4. Escreva a fórmula:y = ____ x + ____ , incluindo os espaços em branco.

5. Preencha o primeiro espaço vazio, o do x, com a inclinação.

6. Preencha o segundo espaço em branco com a interseção com o eixo y.

7. Resolva o problema do exemplo. "Dados os pontos (6, -5) e (8, -12), qual é a equação da reta?"
Método 4 de 5: Quando um ponto e uma linha paralela são dados
1. Determine a inclinação da reta paralela. Lembre-se que a inclinação é o coeficiente de X através do qual y não tem coeficiente.
- Em uma equação como y = 3/4 x + 7, a inclinação é 3/4.
- Em uma equação como y = 3x - 2, a inclinação é 3.
- Em uma equação como y = 3x, a inclinação ainda é 3.
- Em uma equação como y = 7, a inclinação é zero (porque há zero x no problema).
- Em uma equação como y = x - 7, a inclinação é 1.
- Em uma equação como -3x + 4y = 8, a inclinação é 3/4.
- Para encontrar a inclinação de uma equação como essa, basta reorganizá-la de modo que o y é isolado:
- 4a = 3x + 8
- Divida ambos os lados por 4: y = 3/4x + 2

2. Calcule a interseção com o eixo y, usando a inclinação do primeiro passo e a equação b = y - mx.

3. Anote a fórmula:y = ____ x + ____ , com os espaços em branco.

4. Preencha o primeiro espaço vazio, antes do x, com a inclinação que você determinou no passo 1.A coisa notável sobre as linhas paralelas é que elas têm a mesma inclinação, então você acaba com o que começou.

5. Preencha a interseção com o eixo y no segundo espaço vazio.
6. Resolva o problema do exemplo. "Dado o ponto (4, 3) e a reta paralela 5x - 2y = 1; qual é a equação da reta?"
Método 5 de 5: Com um determinado ponto e uma linha perpendicular
1. Encontre a inclinação da linha dada. Confira os exemplos acima para obter mais informações.

2. Encontre o inverso negativo dessa inclinação. Em outras palavras, vire-o e mude o sinal. O ponto com linhas perpendiculares é que elas têm uma inclinação inversa negativa, então você terá que fazer alterações na inclinação antes de poder usá-la.

3. Calcule a interseção com o eixo y usando a inclinação do passo 2 e a equação b = y - mx

4. Anote a fórmula:y = ____ x + ____ , com os espaços em branco.

5. Preencha o primeiro espaço vazio, antes do x, com a inclinação que você calculou no passo 2.

6. Preencha a interseção com o eixo y no segundo espaço vazio.
7. Resolva o problema do exemplo. "Dado (8, -1) ee a perpendicular 4x + 2y = 9; qual é a equação da reta?"
Artigos sobre o tópico "Encontrando a equação de uma reta"
Оцените, пожалуйста статью
Popular