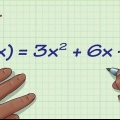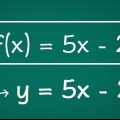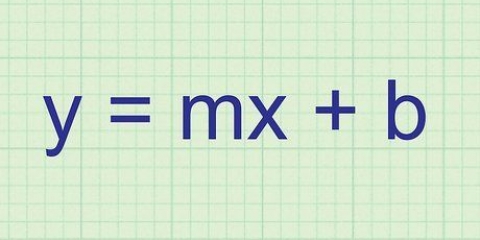está se tornando
está se tornando 
 está se tornando
está se tornando 
 está se tornando
está se tornando  .
.








Se os dois resultados forem iguais, então f(x)=f(-x), e a função original é par. Um exemplo é:  e
e  .
.Esses dois são iguais e, portanto, a função é par. Se cada termo da nova versão da função é o recíproco do termo correspondente da original, então f(x)=-f(-x) e a função é ímpar. Por exemplo:  mas
mas  .
.Observe que se você multiplicar cada termo da primeira função por -1, você torna a segunda função. Então a função original g(x) é ímpar. Se a nova função não corresponder a nenhum desses dois exemplos, ela não é nem par nem ímpar. Por exemplo:  mas
mas  . O primeiro termo é o mesmo em todas as funções, mas o segundo termo é um inverso. Portanto, esta função não é nem par nem ímpar.
. O primeiro termo é o mesmo em todas as funções, mas o segundo termo é um inverso. Portanto, esta função não é nem par nem ímpar.

Você pode testar a simetria selecionando pontos individuais. Se o valor de y de qualquer valor de x for o mesmo que o valor de y de -x, então a função é par. Os pontos escolhidos acima para plotagem  dê os seguintes resultados:
dê os seguintes resultados: (1,3) e (-1,3) (2,9) e (-2,9). Os valores de y correspondentes para x=1 e x=-1, e para x=2 e x=-2, indicam que esta é uma função par. Para um teste melhor, selecionar dois pontos não é evidência suficiente, mas é uma boa indicação. 
Se você escolher um par de valores de teste para x e seus valores correspondentes inversos para -x, deverá obter resultados inversos. Considere o recurso  . Esta função retorna os seguintes pontos:
. Esta função retorna os seguintes pontos:  . O ponto é (1,2).
. O ponto é (1,2). . O ponto é (-1,-2).
. O ponto é (-1,-2). . O ponto é (2,10).
. O ponto é (2,10). . O ponto é (-2,-10).
. O ponto é (-2,-10).Assim f(x)=-f(-x), e você pode concluir que a função é ímpar. 
Escolha um par de valores para x e -x, como segue:  . O ponto para plotar é (1,4).
. O ponto para plotar é (1,4). . O ponto a ser plotado é (-1,-2).
. O ponto a ser plotado é (-1,-2). . O ponto para plotar é (2,10).
. O ponto para plotar é (2,10). . O ponto para plotar é (2,-2).
. O ponto para plotar é (2,-2).Isso já te dá pontos suficientes para notar que não há simetria. Os valores de y para pares opostos de valores de x não são os mesmos, nem são inversos um do outro. Esta função não é par nem ímpar. Você pode ver este recurso,  , pode ser reescrito como
, pode ser reescrito como  . Escrito desta forma, parece que é uma função par porque há apenas um expoente, e esse é um número par. No entanto, este exemplo ilustra que você não pode determinar se uma função é par ou ímpar quando está entre parênteses. Você tem que avaliar a função em termos individuais e então examinar os expoentes.
. Escrito desta forma, parece que é uma função par porque há apenas um expoente, e esse é um número par. No entanto, este exemplo ilustra que você não pode determinar se uma função é par ou ímpar quando está entre parênteses. Você tem que avaliar a função em termos individuais e então examinar os expoentes.
Saber se uma função é par ou ímpar
Contente
Uma maneira de classificar funções é `par`, `ímpar` ou nenhuma. Esses termos referem-se à repetição ou simetria da função. A melhor maneira de descobrir é manipulando algebricamente a função. Você também pode estudar o gráfico da função e procurar a simetria. Depois de saber como classificar os recursos, você também pode prever a aparência de certas combinações de recursos.
Degraus
Método 1 de 2: Testando a função algebricamente

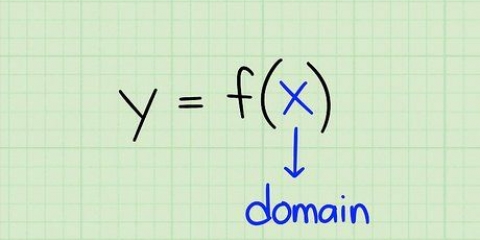
1. Ver variáveis inversas. Em álgebra, o recíproco de uma variável é negativo. Isso é verdade ou a variável da função agora  é ou outra coisa. Se a variável da função original já é negativa (ou uma subtração), então sua recíproca é positiva (ou uma adição). Seguem alguns exemplos de variáveis e suas inversas:
é ou outra coisa. Se a variável da função original já é negativa (ou uma subtração), então sua recíproca é positiva (ou uma adição). Seguem alguns exemplos de variáveis e suas inversas:
 é ou outra coisa. Se a variável da função original já é negativa (ou uma subtração), então sua recíproca é positiva (ou uma adição). Seguem alguns exemplos de variáveis e suas inversas:
é ou outra coisa. Se a variável da função original já é negativa (ou uma subtração), então sua recíproca é positiva (ou uma adição). Seguem alguns exemplos de variáveis e suas inversas: - O inverso de
é
- O inverso de
é
- O inverso de
é
.

2. Substitua cada variável da função por sua inversa. Não altere a função original, exceto o caractere. Por exemplo:
 está se tornando
está se tornando 
 está se tornando
está se tornando 
 está se tornando
está se tornando  .
.
3. Simplifique o novo recurso. Neste ponto, você não precisa se preocupar em resolver a função para um determinado valor numérico. Você apenas simplifica as variáveis para comparar a nova função, f(-x), com a função original, f(x). Lembre-se das regras básicas dos expoentes que dizem que uma base negativa para uma potência par será positiva, enquanto uma base negativa para uma potência ímpar será negativa.








4. Compare as duas funções. Para cada exemplo que você tentar, compare a versão simplificada de f(-x) com a original f(x). Coloque os termos lado a lado para facilitar a comparação e compare os sinais de todos os termos.
 e
e  .
. mas
mas  .
. mas
mas  . O primeiro termo é o mesmo em todas as funções, mas o segundo termo é um inverso. Portanto, esta função não é nem par nem ímpar.
. O primeiro termo é o mesmo em todas as funções, mas o segundo termo é um inverso. Portanto, esta função não é nem par nem ímpar.Método 2 de 2: teste a função graficamente

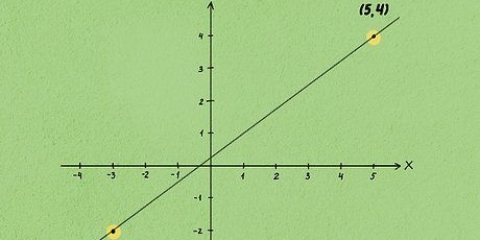
1. Faça o gráfico da função. Use papel quadriculado ou uma calculadora gráfica para representar graficamente a função. Escolha diferentes valores numéricos para  e conecte isso na função para obter o valor resultante de
e conecte isso na função para obter o valor resultante de  calcular. Plote esses pontos no gráfico e depois de traçar vários pontos desenhe uma linha através deles para representar graficamente a função.
calcular. Plote esses pontos no gráfico e depois de traçar vários pontos desenhe uma linha através deles para representar graficamente a função.
 e conecte isso na função para obter o valor resultante de
e conecte isso na função para obter o valor resultante de  calcular. Plote esses pontos no gráfico e depois de traçar vários pontos desenhe uma linha através deles para representar graficamente a função.
calcular. Plote esses pontos no gráfico e depois de traçar vários pontos desenhe uma linha através deles para representar graficamente a função. - Ao traçar os pontos, preste atenção aos valores positivos e negativos correspondentes para
. Por exemplo, se você estiver lidando com a função
, então você plota os seguintes valores:
. Isso resulta no ponto
.
. Isso resulta no ponto
.
. Isso resulta no ponto
.
. Isso resulta no ponto
.

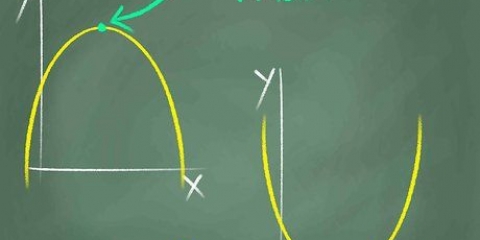
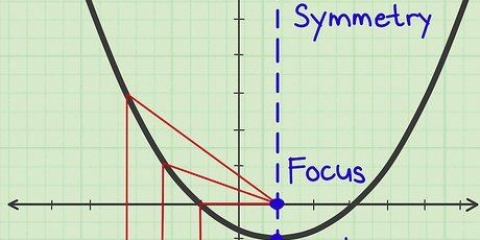
2. Observe a simetria ao longo do eixo y. Ao olhar para uma função, a simetria irá sugerir uma imagem espelhada. Se você perceber que a parte do gráfico do lado direito (positivo) do eixo y corresponde à parte do gráfico do lado esquerdo (negativo) do eixo y, então o gráfico é simétrico em relação ao eixo y. Se uma função é simétrica em relação ao eixo y, então a função é par.
 dê os seguintes resultados:
dê os seguintes resultados:
3. Teste de simetria da origem. A origem é o ponto central (0,0). Simetria de origem significa que um resultado positivo para um valor x escolhido corresponderá a um resultado negativo para -x e vice-versa. Funções ímpares exibem simetria de origem.
 . Esta função retorna os seguintes pontos:
. Esta função retorna os seguintes pontos: . O ponto é (1,2).
. O ponto é (1,2). . O ponto é (-1,-2).
. O ponto é (-1,-2). . O ponto é (2,10).
. O ponto é (2,10). . O ponto é (-2,-10).
. O ponto é (-2,-10).
4. Veja se não há simetria. O último exemplo é uma função sem simetria em ambos os lados. Se você olhar para o gráfico, verá que não é uma imagem espelhada no eixo y ou em torno da origem. Veja o recurso  .
.
 .
. . O ponto para plotar é (1,4).
. O ponto para plotar é (1,4). . O ponto a ser plotado é (-1,-2).
. O ponto a ser plotado é (-1,-2). . O ponto para plotar é (2,10).
. O ponto para plotar é (2,10). . O ponto para plotar é (2,-2).
. O ponto para plotar é (2,-2). , pode ser reescrito como
, pode ser reescrito como  . Escrito desta forma, parece que é uma função par porque há apenas um expoente, e esse é um número par. No entanto, este exemplo ilustra que você não pode determinar se uma função é par ou ímpar quando está entre parênteses. Você tem que avaliar a função em termos individuais e então examinar os expoentes.
. Escrito desta forma, parece que é uma função par porque há apenas um expoente, e esse é um número par. No entanto, este exemplo ilustra que você não pode determinar se uma função é par ou ímpar quando está entre parênteses. Você tem que avaliar a função em termos individuais e então examinar os expoentes.Pontas
- Se todas as formas de uma variável na função têm expoentes pares, então a função é par. Se todos os expoentes são ímpares, então a função é ímpar no geral.
Aviso
- Este artigo se aplica apenas a funções com duas variáveis, que podem ser representadas graficamente em um sistema de coordenadas bidimensional.
Artigos sobre o tópico "Saber se uma função é par ou ímpar"
Оцените, пожалуйста статью
Similar
Popular
Novo