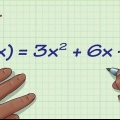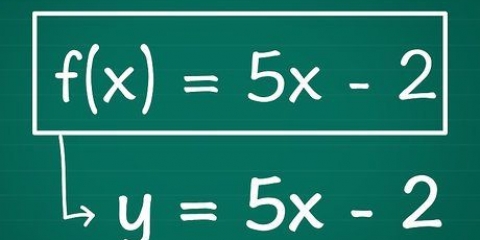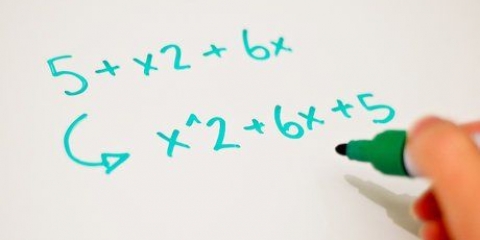Por exemplo: a função padrão f(x) = 2x +16x + 39. Aqui temos a = 2, b = 16 e c = 39. Em notação de vértice: f(x) = 4(x - 5) + 12. Aqui temos a = 4, h = 5 e k = 12. 
Exemplo 1. (f(x) = 2x +16x + 39), h = -b/2a = -16/2(2). Resolvendo isso, vemos que h = -4. Exemplo 2. (f(x) = 4(x - 5) + 12), vemos imediatamente que h = 5. 
Vimos por exemplo 1 que h = -4. Agora, para encontrar k, resolvemos essa equação inserindo esse valor de h na equação, para a variável x: k = 2(-4) + 16(-4) + 39. k = 2(16) - 64 + 39. k = 32 - 64 + 39 = 7 Do exemplo 2 sabemos que o valor de k é igual a 12, sem a necessidade de cálculo. 
No exemplo 1, a parte superior do gráfico é (-4,7). Desenhe o ponto em seu gráfico e certifique-se de nomear as coordenadas corretamente. No exemplo 2, o topo é (5,12). Então do ponto (0,0) você vai 5 lugares para a direita e depois 12 para cima. 
No caso do exemplo 1, o eixo de simetria é a linha paralela ao eixo y e que passa pelo ponto (-4, 7). Embora não faça parte da parábola em si, destacar levemente esta diretriz pode mostrar o quão simétrica é a curva da parábola. 
No exemplo 1 estamos lidando com a função (f(x) = 2x +16x + 39), e esta é, portanto, uma parábola de vale, pois a = 2 (positiva). No exemplo 2 estamos lidando com a função f(x) = 4(x - 5) + 12), e esta também é uma parábola de vale porque a = 4 (positiva). 
Determine que f(x) = 0 e resolva a equação. Este método pode funcionar para equações quadráticas simples, especialmente na forma de vértice, mas você descobrirá que fica cada vez mais difícil à medida que as funções se tornam mais complexas. Abaixo estão alguns exemplos. f(x) = 4(x - 12) 0 = 4(x - 12) - 4 4 = 4(x - 12) 1 = (x - 12) SqRt(1) = (x - 12) +/- 1 = x -12. x = 11 e 13 são as intersecções com o eixo x da parábola. Fatore a equação. Algumas equações da forma ax + bx + c podem ser facilmente reescritas como (dx + e)(fx +g), onde dx × fx = ax, (dx × g + fx × e) = bx, e e × g = c. Neste caso, os x-intercepts são os valores de x onde cada termo dentro dos parênteses se torna 0. Por exemplo: x + 2 x + 1 = (x + 1)(x + 1) Neste caso, o ponto de interseção é igual a -1 porque, quando preenchido com os dois fatores, resulta em zero. Use a fórmula abc. Se não for fácil descobrir as interseções ou fatorar a equação, use o "fórmula abc" que se destina especialmente a este. Suponha uma equação na forma ax + bx + c. Em seguida, insira os valores de a, b e c na fórmula x = (-b +/- SqRt(b - 4ac))/2a. Observe que isso geralmente fornece duas respostas para x, o que é bom - isso significa apenas que sua parábola tem duas interseções com o eixo x. Aqui está um exemplo: -Insira 5x + 1x + 10 na equação da seguinte forma: x = (-1 +/- SqRt(1 - 4(-5)(10)))/2(-5) x = (-1 +/- SqRt(1 + 200))/-10 x = (-1 +/- SqRt(201))/-10 x = (-1 +/- 14,18)/-10 x = (13,18/-10) e (-15,18/-10). As interseções da parábola com o eixo x são aproximadamente x = -1.318 e 1.518 Como no exemplo 1 com a equação 2x + 16x + 39, ficará assim: x = (-16 +/- SqRt(16 - 4(2)(39))))/2(2) x = (-16 +/- SqRt(256 - 312))/4 x = (-16 +/- SqRt(-56)/-10 Como não é possível encontrar a raiz quadrada de um número negativo, sabemos que não existem interseções com o eixo x para essa parábola em particular. 
Por exemplo, sabemos que nossa equação quadrática 2x + 16x + 39 tem um ponto de interseção y = 39, mas também podemos encontrar isso da seguinte forma: f(x) = 2x + 16x + 39 f(x) = 2(0) + 16(0) + 39 f(x) = 39. A intersecção da parábola com o eixo y: y = 39. Como indicado acima, podemos ler facilmente a interseção porque y = c. A equação 4(x - 5) + 12 tem uma interseção com o eixo y que pode ser encontrada da seguinte forma: f(x) = 4(x - 5) + 12 f(x) = 4(0 - 5) + 12 f(x) = 4(-5) + 12 f(x) = 4(25) + 12 f(x) = 112. A interseção com o eixo y: y = 112. 
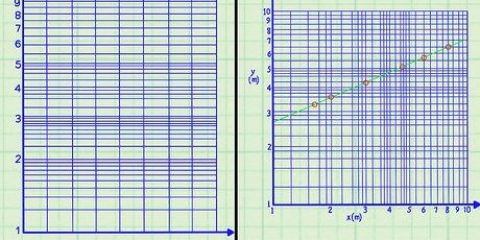
Vamos dar outra olhada na equação x + 2x + 1. Já sabemos que a única interseção com o eixo x é (-1.0). Como ele é apenas tangente ao eixo x neste ponto, podemos inferir que o vértice do gráfico é igual a este ponto. Até agora só temos um ponto desta parábola – não o suficiente para poder desenhar um gráfico. Vamos encontrar mais alguns pontos para ter certeza de que temos mais valores. Vamos tentar encontrar os valores de y associados aos seguintes valores de x: 0, 1, -2 e -3. x=0: f(x) = (0) + 2(0) + 1 = 1. Então o ponto é (0,1). x=1: f(x) = (1) + 2(1) + 1 = 4. Então o ponto é (1,4). x=-2: f(x) = (-2) + 2(-2) + 1 = 1. Então o ponto é (-2.1). x=-3: f(x) = (-3) + 2(-3) + 1 = 4. Então o ponto é (-3,4). Coloque esses pontos no gráfico e desenhe sua parábola. Observe que a parábola é completamente simétrica - se você conhece os pontos de um lado do gráfico, geralmente pode economizar muito trabalho usando esses pontos para encontrar os pontos do outro lado do eixo de simetria.
Representando graficamente uma função
Como um gráfico vê uma equação quadrática ax + bx + c, também qualquer escrito comoa(x - h) + k, parece uma curva suave em forma de U. Isso é o que chamamos de parábola. A representação gráfica de uma equação quadrática envolve encontrar o vértice, a direção e, muitas vezes, as interseções com o eixo x e o eixo y. No caso da equação quadrática relativamente simples, também pode ser suficiente inserir vários valores para x para indicar esses pontos no sistema de coordenadas, após o que a parábola pode ser desenhada. Vá para a etapa 1 para começar.
Degraus

1. Determine que tipo de equação quadrática você tem. Isso pode ser escrito de duas maneiras: a notação padrão e a notação de vértice (outra maneira de escrever a fórmula da raiz quadrada). Você pode usar ambos para fazer um gráfico de uma equação quadrática, mas esse processo é um pouco diferente em ambos os casos. Normalmente você encontrará o formulário padrão, mas certamente não faz mal aprender a usar os dois formulários. As duas formas de uma equação quadrática são: A forma do vértice. Aqui a equação quadrática é escrita como: f(x) = a(x - h) + k onde a, h e k são números reais e a não é igual a zero. Essa forma é chamada de vértice porque h e k se referem diretamente ao vértice de sua parábola no ponto (h,k). Dois exemplos de equações em forma de vértice são f(x) = 9(x - 4) + 18 e -3(x - 5) + 1 Para poder fazer um gráfico dessas equações, primeiro determinamos o topo (h,k) do gráfico. Na equação padrão, você pode encontrar isso via: h = -b/2a e k = f(h), enquanto já é dado na forma de vértice porque h e k ocorrem na equação.
- A forma padrão. Aqui a equação quadrática é escrita como: f(x) = ax + bx + c onde a, b e c são números reais e a não é igual a zero.
- Dois exemplos de equações quadráticas padrão: f(x) = x + 2x + 1 e f(x) = 9x + 10x -8.

2. Determine suas variáveis. Para resolver uma equação quadrática, geralmente é necessário determinar as variáveis a, b e c (ou a, h e k). Um problema comum lhe dará uma equação quadrática na forma padrão, mas a notação de vértice também pode ocorrer.

3. Calcular h. Na notação de vértice o valor de h já é dado, mas na notação padrão este valor ainda não foi calculado. Lembre-se que para a equação padrão, h = -b/2a.

4. Calcular k. Como com h, k já é conhecido para equações na forma de vértice. Para equações em notação padrão, lembre-se de que k = f(h). Em outras palavras, você pode encontrar k substituindo cada variável x pelo valor de h.

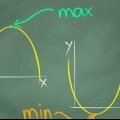
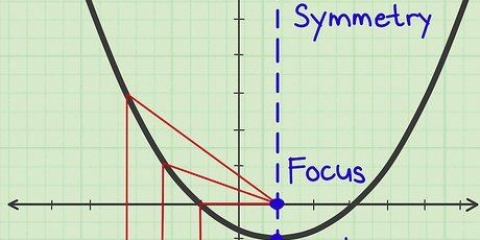
5. Desenhe a parte superior ou inferior do gráfico. A crista ou vale da sua parábola é o ponto (h, k) - h representa a coordenada x e k representa a coordenada y. A crista é o centro de sua parábola - o ponto mais alto ou mais baixo, a crista ou a depressão, de um gráfico na forma de um "VOCÊS" ou vice-versa. Ser capaz de determinar o vértice de uma parábola é uma parte essencial de ser capaz de desenhar um gráfico correto – muitas vezes determinar o vértice de uma parábola é parte de um problema de matemática na escola.

6. Desenhe o eixo de simetria da parábola. O eixo de simetria de uma parábola é a linha que intercepta a figura no meio e a divide exatamente ao meio. Um lado do gráfico é espelhado ao longo desta linha no outro lado do gráfico. Para equações quadráticas da forma ax + bx + c ou a(x - h) + k, este eixo é a linha paralela ao eixo y que passa pelo vértice da parábola.

7. Determine a direção da parábola. Depois de descobrir qual é o topo da parábola, é necessário saber se você está lidando com uma parábola de montanha ou uma parábola de vale, ou seja, se a abertura está na parte inferior ou na parte superior. Felizmente isso é muito simples. E se "uma" positivo você está lidando com uma parábola do vale; é "uma" negativo então é uma parábola de montanha (com a abertura na parte inferior)

8. Determine, se necessário, as interseções da parábola. Muitas vezes, em problemas de matemática, você é solicitado a fornecer as interseções da parábola com o eixo x (estas são "zero", uma ou dois pontos onde a parábola intercepta ou toca o eixo x). Mesmo que não sejam solicitados, esses pontos são muito importantes para poder traçar um gráfico preciso. Mas nem todas as parábolas se cruzam com o eixo x. Se você está lidando com uma parábola de vale e o ponto do vale está acima do eixo x ou, no caso de uma parábola de montanha, logo abaixo do eixo x, então simplesmente não há interseções a serem encontradas. Em caso afirmativo, use um dos seguintes métodos:

9. Se necessário, determine a interseção da parábola com o eixo y. Muitas vezes não é necessário, mas às vezes é necessário encontrar esse ponto de interseção, por exemplo, para um problema de matemática. Isso é bastante fácil - defina o valor de x para 0 e resolva a equação para f(x) ou y, que fornece o valor de y do ponto onde a parábola cruza com o eixo y. A diferença com as interseções através do eixo x é que com o eixo y sempre há apenas um ponto de interseção. Nota - para equações padrão, a interseção com o eixo y está em y = c.

10. Se você achar necessário, primeiro desenhe pontos extras e depois todo o gráfico. Agora você deve ter um pico ou vale, uma direção, interseções com o eixo x e possivelmente com o eixo y de sua equação. A partir deste ponto, você pode tentar desenhar a parábola usando esses pontos ou tentar encontrar mais pontos para tornar o gráfico mais preciso. A maneira mais fácil de fazer isso é simplesmente preencher um número de valores x, que retorna um número de valores y. Muitas vezes você será solicitado (pelo professor) a calcular primeiro um número de pontos antes de poder desenhar a parábola.
Pontas
- Arredonde os números se necessário ou use frações. Isso pode ajudar a exibir um gráfico corretamente.
- Observe que se, para a função f(x) = ax + bx + c, b ou c forem iguais a zero, esses termos desaparecerão. Por exemplo, 12x + 0x + 6 é igual a 12x + 6 porque 0x é igual a 0.
Artigos sobre o tópico "Representando graficamente uma função"
Оцените, пожалуйста статью
Popular