Ensine a classe a contar em pares, três, cinco e depois dezenas. Este é um conceito essencial para os alunos entenderem antes de explicar o sistema de valor posicional para eles. Tente incutir neles um forte senso de "dez". A matemática ocidental moderna usa o número dez como base, por isso será muito mais fácil para as crianças aprenderem os sistemas mais complexos se estiverem acostumadas a pensar dessa maneira. Ensine os alunos a agrupar instintivamente os números em conjuntos de dez. 

Demonstre isso com um exemplo: `1` é o número um e `7` é o número sete. Se você os vê como um grupo um ao lado do outro, eles formam o número `17` dezessete. Da mesma forma, no número 35 você vê os dígitos `3` e 5`. Dê vários outros exemplos para tornar o ponto claro. 


Ilustre as `unidades`. Marque ou cubra cada número com um `3` no lugar das `unidades`: 3, 13, 23, 33, 43, 53, 63, 73, 83, 93. Explique as "dezenas". Peça ao grupo que designe qualquer número com um “2” como “dezenas”: 20, 21, 22, 23, 24, 25, 26, 27, 28, 29. Explique que o `3` em `23` está empilhado no topo do `20` indicado pelo `2`. Ensine as crianças a ler as "dezenas" como um gatilho. 
A memória é predominantemente visual, e o conceito de valor posicional pode permanecer abstrato até que você o coloque em termos visuais. A esse respeito, os símbolos numéricos podem ser abstratos mesmo para crianças pequenas! Procure maneiras de enquadrar a contagem de grupos e os valores de posição para que pareçam simples, táteis e intuitivos. 



Como uma adição simples, peça aos alunos que coloquem três fichas azuis (dezenas) e seis fichas brancas (unidades) lado a lado. Pergunte à classe que número isso produz. (é 36!) Continue com o mesmo número. Peça aos seus alunos para adicionar cinco fichas brancas ao número 36. Pergunte aos seus alunos que número eles têm agora. (é 41!) Em seguida, você remove um chip azul e pergunta aos alunos que número ele diz. (é 31!)
Explicando o sistema de valor posicional
Contente
O sistema de valor posicional, a ideia de que o valor de um dígito (0-9) depende de sua posição em um número, é um conceito fundamental em matemática. Como essa ideia é tão óbvia para alguém que já a entende, pode ser difícil ensiná-la a outras pessoas. No entanto, quando seus alunos começarem a entender isso, eles ficarão ansiosos para usar sua nova habilidade e aprender mais sobre conceitos matemáticos mais complicados.
Degraus
Parte 1 de 3: Apresentando o básico

1. Saiba quando explicar o sistema de valor posicional. Se você tem que trabalhar dentro de um currículo pré-definido como professor, talvez já tenha uma ideia de como o valor posicional pode se encaixar no conjunto das aulas. Se você dá aulas particulares ou educação em casa, provavelmente trabalha em uma estrutura mais flexível. Ensine às crianças o valor posicional dos números logo após aprender a contar e fazer somas simples de mais e menos – geralmente na segunda ou terceira séries. Uma compreensão do sistema de valores posicionais estabelecerá as bases para que essas crianças mergulhem em conceitos matemáticos mais complexos.

2. Introduzir o conceito de contagem em grupos de números. A maioria das crianças só aprendeu a contar com números: um... dois... três... quatro. Isso é suficiente para adição e subtração simples, mas não é suficiente para dar aos alunos uma base sólida para a compreensão de funções mais complexas. Antes de ensinar as crianças a dividir números grandes em valores posicionais, pode ser útil ensiná-los a agrupar números pequenos em números grandes.

3. Repense a ideia de valor de lugar. Dê a si mesmo um curso de atualização. Certifique-se de entender completamente o conceito antes de tentar ensiná-lo a um grupo de jovens aprendizes. O valor posicional, de forma simples, é a ideia de que o valor de um dígito (0-9) depende de seu `lugar` ou posição em um número.

4. Explique a diferença entre os números e os números. Os números são os dez símbolos que compõem um inteiro: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Combinamos esses números para formar qualquer outro número. Um dígito pode ser um número (por exemplo, o número 7), mas somente se não estiver agrupado com outro dígito. Quando dois ou mais dígitos são agrupados, a ordem desses dígitos determina o número maior.
Parte 2 de 3: Educação com exemplos visuais

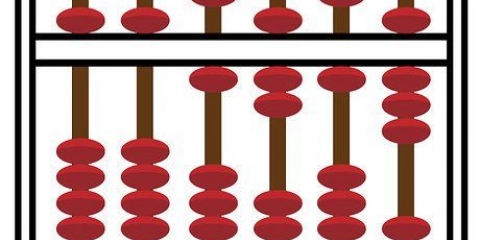
1. Mostre às crianças que é mais fácil contar em grupos de dez. Use 30-40 pequenos objetos contáveis e bastante simples: seixos, bolinhas de gude, borrachas. Espalhe-os em uma mesa para seus alunos. Explique que na matemática moderna usamos o número 10 como base. Organize os objetos em diferentes grupos de dez e conte-os na frente da classe. Mostre aos alunos que quatro grupos de 10 pedras são iguais a 40.

2. Traduza o exemplo das pedras em números escritos. Esboce o conceito em uma placa. Primeiro, desenhe uma tabela simples em duas colunas, escreva o número 1 como título no canto superior direito da tabela. Em seguida, escreva 10 como título no canto superior esquerdo. Escreva um 0 na (coluna da direita) sob o título `1` e um 4 na coluna da esquerda com o título `10`. Agora explique à classe que cada número que você fez com as pedrinhas tem seu próprio `lugar`.

3. Use um quadro numérico para ilustrar os fundamentos dos valores posicionais. Crie uma `tabela numérica` onde todos os números de 1 a 100, numerados sequencialmente, são mostrados. Mostre aos seus alunos a interação entre os números de 0 a 9 e os números de 10 a 100. Explique que todo número de 10 a 99 é na verdade dois números, com um número na casa das "unidades" e um número na casa das "dezenas". Mostre como o número `4` é o mesmo que `4` no lugar das `unidades`, mas atua como um prefixo para o número `40` quando está no lugar das `dezenas`.

4. Experimente outras ferramentas de aprendizagem visual. Você pode organizar os objetos físicos ou desenhar em um quadro. Você pode explicar o valor posicional contando dinheiro, que os alunos provavelmente já aprenderam a associar aos valores numéricos em escala. Um exercício divertido e interativo é deixar os próprios alunos brincarem de `grupos` de valores.

5. Usar cores. Experimente lápis de cor ou marcadores de cores diferentes para explicar visualmente o sistema de valor posicional. Por exemplo, escreva números diferentes com um marcador preto para as `unidades` e com um marcador azul para as `dezenas`. Assim, você escreveria o número 40 com um `4` azul e um `0` preto. Repita este truque com uma grande variedade de números para mostrar que o sistema de valor posicional se aplica a todos os números.
Parte 3 de 3: Usando um exemplo interativo

1. Explique com fichas de poker. Primeiro divida as fichas de pôquer entre todos os alunos. Diga à classe que as fichas de pôquer brancas representam as "unidades", as azuis as "dezenas" e as fichas de pôquer vermelhas as "centenas". Em seguida, mostre à classe como fazer números indicando o valor posicional, usando as fichas. Dê-lhes um número (por exemplo, 7) e coloque uma ficha branca no lado direito da sua mesa de trabalho.
- Nomeie outro número – por exemplo, 30. Três fichas azuis representam o 3 (no lugar das `dezenas`) e as fichas brancas representam o 0 (no lugar das `unidades`).
- Você não precisa necessariamente usar fichas de pôquer. Quase qualquer coleção de objetos pode representar os três valores fundamentais das placas, desde que cada grupo (cor das fichas, etc.).) é padrão, homogêneo e fácil de reconhecer.

2. Tenha as fichas de troca de classe. Esta é uma forma de ilustrar como os valores posicionais mais altos podem ser divididos em valores posicionais mais baixos. Uma vez que os alunos tenham uma compreensão completa do valor posicional, ensine à classe como trocar as fichas de "unidades" brancas por fichas de "dezenas" azuis e fichas de "dezenas" por fichas de "centenas" vermelhas. Pergunte à turma, `quantas fichas azuis eu recebo se eu quiser trocar 16 fichas brancas? Se eu trocar três fichas azuis, quantas fichas brancas posso obter?"

3. Demonstrar adição e subtração com as fichas de pôquer.Só lide com esse conceito depois que os alunos dominarem a troca de fichas de pôquer. Pode ajudar dar um exemplo primeiro.
Pontas
- Se houver alunos participando de programas de aprendizado rápido, dê a eles problemas de valor posicional mais desafiadores. Ensine-os que o Maya usa um valor base de 20. Mostre que eles usaram pontos, barras e uma forma de concha como números. Os pontos representavam as unidades, as barras os cincos e as conchas os zeros. No sistema maia, o número 53 foi escrito como uma potência de 20: (2 x 20 + 13 = 53).
Avisos
- Diminua a velocidade se perceber que alguns alunos têm problemas para agrupar números. Traga-os de volta a um conceito de valor de lugar mais simples.
Artigos sobre o tópico "Explicando o sistema de valor posicional"
Оцените, пожалуйста статью
Popular