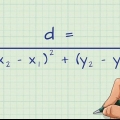Calculando o Valor Absoluto de um Número: 15 Passos (com Imagens)

Contente

Degraus
- Método 1 de 2: Determinar o valor absoluto
- Método 2 de 2: Resolvendo equações complexas com valores absolutos (equações com `i`)
Pontas

O valor absoluto de um número é fácil de encontrar, e a teoria por trás dele é importante para resolver equações com um valor absoluto. Cada valor absoluto é uma medida de quão longe esse número está de zero. Se você pensar em uma reta numérica, com o zero no meio, poderá descobrir a que distância o número em questão está desse zero.

Degraus

Método 1 de 2: Determinar o valor absoluto

Imagem intitulada Encontre o valor absoluto de um número Passo 1

1. Lembre-se que o valor absoluto é a distância de um número de zero. Um valor absoluto é a distância do número a zero ao longo de uma reta numérica. qualquer,

| - 4 |

${estilo de exibição |-4|}$ então simplesmente indica a que distância -4 está de zero. Como a distância é sempre um número de posição (você não pode se mover em passos `negativos`, apenas em outra direção), o resultado do valor absoluto é sempre positivo.

Imagem intitulada Encontre o valor absoluto de um número Passo 2

2. Torne o número dentro das barras de valor absoluto positivo. Simplificando, o valor absoluto torna qualquer número positivo. É útil para medir distâncias, ou determinar valores em questões financeiras, trabalhando com números negativos como dívidas ou empréstimos.

Imagem intitulada Encontre o valor absoluto de um número Passo 3

3. Use barras verticais simples para indicar um valor absoluto. O formato para um valor absoluto é fácil. Linhas simples (encontradas perto da tecla Enter em um teclado) em torno de um número ou expressão, como

| n |, | 3 + 5 |, | - 72 |

${estilo de exibição |n|,|3+5|,|-72|}$ , indica um valor absoluto.

| 2 |

${estilo de exibição |2|}$ é `o valor absoluto de 2.`

Imagem intitulada Encontre o valor absoluto de um número Passo 4

4. Omitir sinais de menos para o número dentro das marcas de valor absoluto. Por exemplo: |-5| então se torna |5|.

Imagem intitulada Encontre o valor absoluto de um número Passo 5

5. Omitir as marcas de valor absoluto. O número que resta é a resposta, então |-5| torna-se |5| e depois 5. O seguinte é tudo o que você precisa fazer:

| - 5 | = 5

${estilo de exibição |-5|=5}$

Imagem intitulada Encontre o valor absoluto de um número Passo 6

6. Simplifique a expressão dentro do valor absoluto. É uma expressão simples, como

| - 10 |

${estilo de exibição |-10|}$ , então você pode apenas torná-lo positivo. Mas uma expressão como

| (- 4 * 5) + 3 - 2 |

${estilo de exibição |(-4*5)+3-2|}$ deve ser simplificado antes que você possa encontrar seu valor absoluto. A ordem fixa de operações ainda se aplica:

Atribuição:

| (- 4 * 5) + 3 - 2 |

${estilo de exibição |(-4*5)+3-2|}$

Simplifique entre parênteses:

| (- 20) + 3 - 2 |

${estilo de exibição |(-20)+3-2|}$

Adicionar e subtrair:

| - 19 |

${estilo de exibição |-19|}$

Faça tudo dentro do valor absoluto positivo:

| 19 |

${estilo de exibição |19|}$

Resposta final: 19

Imagem intitulada Encontre o valor absoluto de um número Passo 7

7. Sempre use esta ordem de operações antes de calcular o valor absoluto. Ao elaborar equações mais longas, você faz todo o trabalho necessário antes de determinar o valor absoluto. Não tente simplificar valores absolutos até que tudo seja somado, subtraído e dividido corretamente. Por exemplo:

Atribuição:

1 + 2 + | 4 - 7 | 5 * | - 3 * 2 |

${displaystyle {frac {1+2+|4-7|}{5*|-3*2|}}}$

Faça a ordem das operações dentro e fora do valor absoluto:

3 + | - 3 | 5 * | - 6 |

${estilo de exibição {frac {3+|-3|}{5*|-6|}}}$

Determine os valores absolutos:

3 + (3) 5 * (6)

${displaystyle {frac {3+(3)}{5*(6)}}}$

Ordem de operações:

\frac{6}{30}

${displaystyle {frac {6}{30}}}$

Simplifique a resposta final: $\frac{1}{5}$ ${frac{1}{5}}$

Imagem intitulada Encontre o valor absoluto de um número Passo 8

8. Continue trabalhando em alguns exemplos de exercícios para pegar o jeito. Calcular o valor absoluto de um número é muito fácil, mas isso não significa que fazer problemas práticos não seria útil para aprimorar seu conhecimento:

| 12 |

${estilo de exibição |12|}$ =

12

${estilo de exibição 12}$

| - 24 |

${estilo de exibição |-24|}$ =

24

${estilo de exibição 24}$

| 3 + 2 - 11 + 5 - 6 |

${estilo de exibição |3+2-11+5-6|}$ =

7

$7$

Método 2 de 2: Resolvendo equações complexas com valores absolutos (equações com `i`)

Imagem intitulada Encontre o valor absoluto de um número Passo 9

1. Tenha cuidado ao lidar com equações complexas envolvendo números imaginários, como `i` ou -1{displaystyle {sqrt {-1}}} ${displaystyle {sqrt {-1}}}$ , e resolvê-los separadamente. Você não pode encontrar o valor absoluto de números imaginários da mesma forma que pode encontrar números racionais. Você pode encontrar o valor absoluto de uma equação complexa trabalhando na fórmula da distância. Pegue a expressão

| 3 - 4 eu |

${estilo de exibição |3-4i|}$ como um exemplo.

Atribuição: $| 3 - 4 eu |$ ${estilo de exibição |3-4i|}$
Prestar atenção: Se você usar uma expressão como $\sqrt{- 1}$ ${displaystyle {sqrt {-1}}}$ você pode substituí-lo por `i.` A raiz quadrada de -1 é um número imaginário, i. $| eu | = 1$ ${estilo de exibição |i|=1}$

Imagem intitulada Encontre o valor absoluto de um número Passo 10

2. Encontre os coeficientes da equação complexa. Tome 3-4i como a equação de uma linha. O valor absoluto é a distância até zero, então você determina a distância até zero para o ponto (3, -4) nesta linha.Os coeficientes são simplesmente os dois números que não são `i`. Embora o número ao lado do i seja geralmente o segundo número, não importa ao resolver. Pratique isso com os seguintes coeficientes:

| 1 + 6 eu |

${estilo de exibição |1+6i|}$ = (1, 6)

| 2 - eu |

${estilo de exibição |2-i|}$ = (2, -1)

| 6 eu - 8 |

${estilo de exibição |6i-8|}$ = (-8, 6)

Imagem intitulada Encontre o valor absoluto de um número Passo 11

3. Remova os símbolos de valor absoluto da equação. Agora você só precisa dos coeficientes. Lembre-se que você determina a distância da equação de zero. Como você usará a fórmula da distância na próxima etapa, isso é o mesmo que determinar o valor absoluto.

Imagem intitulada Encontre o valor absoluto de um número Passo 12

4. Quadrado de ambos os coeficientes. Para determinar a distância, você usa a fórmula da distância, também conhecida como

\sqrt{X} 2 + y^{2}

${displaystyle {sqrt {x^{2}+y^{2}}}}$ . Então, como primeiro passo, você tem que elevar ao quadrado ambos os coeficientes da equação complexa. Continuamos com o exemplo:

| 3 - 4 eu |

${estilo de exibição |3-4i|}$ :

Coeficientes: (3, -4)

Fórmula da distância:

\sqrt{3} 2 + (- 4)^{2}

${displaystyle {sqrt {3^{2}+(-4)^{2}}}}$

Esquadre os coeficientes: `

\sqrt{9 + 16}

${displaystyle {sqrt {9+16}}}$

Prestar atenção: Pratique a fórmula da distância novamente se você não entender. Observe que elevar ao quadrado os dois números os torna positivos, essencialmente dando a você o valor absoluto.

Imagem intitulada Encontre o valor absoluto de um número Passo 13

5. Coloque o produto dos números sob o radical. O sinal de radical indica que você está subtraindo a raiz quadrada do número abaixo dele. Agora some os números primeiro, sem fazer nada sobre o sinal de radical.

Coeficientes: (3, -4)

Fórmula da distância:

\sqrt{3} 2 + (- 4)^{2}

${displaystyle {sqrt {3^{2}+(-4)^{2}}}}$

Esquadre os coeficientes:

\sqrt{9 + 16}

${displaystyle {sqrt {9+16}}}$

Some o produto dos coeficientes:

\sqrt{25}

${displaystyle {sqrt {25}}}$

Imagem intitulada Encontre o valor absoluto de um número Passo 14

6. Tire a raiz quadrada para sua resposta final. Você só precisa simplificar a equação para a resposta final. Esta é a distância do seu `ponto` em uma reta numérica imaginária até o ponto zero. Se não houver raiz quadrada, basta deixar a resposta da última etapa sob o sinal de radical - esta é uma resposta correta.

Coeficientes: (3, -4)

Fórmula da distância:

\sqrt{3} 2 + (- 4)^{2}

${displaystyle {sqrt {3^{2}+(-4)^{2}}}}$

Esquadre os coeficientes:

\sqrt{9 + 16}

${displaystyle {sqrt {9+16}}}$

Some o produto dos coeficientes:

\sqrt{25}

${displaystyle {sqrt {25}}}$

Subtraia a raiz quadrada para a resposta final: 5

$| 3 - 4 eu | = 5$ ${estilo de exibição |3-4i|=5}$

Imagem intitulada Encontre o valor absoluto de um número Passo 15

7. Experimente alguns exercícios práticos. Clique com o mouse diretamente atrás das perguntas para ver as respostas, em branco.

| 1 + 6 eu |

${estilo de exibição |1+6i|}$ = √37

| 2 - eu |

${estilo de exibição |2-i|}$ = √5

| 6 eu - 8 |

${estilo de exibição |6i-8|}$ = 10

Pontas

Se você tiver uma variável dentro de um valor absoluto, não poderá remover os sinais de valor absoluto usando este método, porque se o valor da variável for negativo, o valor absoluto o tornará positivo.
Se você tiver uma expressão dentro de um valor absoluto, simplifique a expressão antes de determinar seu valor absoluto.
Quando um número positivo está dentro dos marcadores de valor absoluto, a resposta é sempre esse número.
Você precisa de um método diferente para resolver equações de valor absoluto com x e y, embora a teoria por trás do valor absoluto seja usada como base.
Um valor absoluto nunca pode ser um número negativo, portanto, se você vir algo como | 2 - 4x| = -7, então você sabe que esta equação é falsa sem ter que resolvê-la.