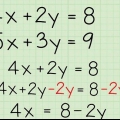2x - 2x = 0 4a - 2a = 2a 8 - 2 = 6 2x + 4y = 8-(2x + 2y = 2)=0 +2y = 6 
2a = 6 Divida 2y e 6 por 2 e obtenha y = 3 
Insira y = 3 na equação 2x + 2y = 2 e resolva para x. 2x + 2(3) = 2 2x + 6 = 2 2x = -4 x = - 2 Você resolveu o sistema de equações por subtração. (x, y) = (-2, 3) 
Preencha (-2, 3) para (x, y) na equação 2x + 4y = 8. 2(-2) + 4(3) = 8 -4 + 12 = 8 8 = 8 Preencha (-2, 3) para (x, y) na equação 2x + 2y = 2. 2(-2) + 2(3) = 2 -4 + 6 = 2 2 = 2 

3x + x = 4x 6a + -6a = 0 8 + 4 = 12 Se você combinar isso, obterá um novo produto: 3x + 6a = 8 +(x - 6y = 4) = 4x + 0 = 12 
4x + 0 = 12 4x = 12 Divida 4x e 12 por 3 para obter x = 3 
Insira x = 3 na equação x - 6y = 4 para encontrar y. 3 - 6 anos = 4 -6 anos = 1 Divida -6y e 1 por -6 para obter y = -1/6. Você resolveu o sistema de equações com adição. (x, y) = (3, -1/6) 
Preencha (3, -1/6) para (x, y) na equação 3x + 6y = 8. 3(3) + 6(-1/6) = 8 9 - 1 = 8 8 = 8 Preencha (3, -1/6) para (x, y) na equação x - 6y = 4. 3 - (6 * -1/6) =4 3 - - 1 = 4 3 + 1 = 4 4 = 4 

2 (2x - y = 2) 4x - 2a = 4 
3x + 2a = 10 + 4x - 2a = 4 7x + 0 = 14 7x = 14 

x = 2 ---> 2x - y = 2 4 - y = 2 -y = -2 y = 2 Você resolveu o sistema de equações usando a multiplicação. (x, y) = (2, 2) 
Preencha (2, 2) para (x, y) na equação 3x + 2y = 10. 3(2) + 2(2) = 10 6 + 4 = 10 10 = 10 Preencha (2, 2) para (x, y) na equação 2x - y = 2. 2(2) - 2 = 2 4 - 2 = 2 2 = 2 

x = 2 - 4y --> 2x + 3a = 9 2(2 - 4a) + 3a = 9 4 - 8 anos + 3 anos = 9 4 - 5 anos = 9 -5a = 9 - 4 -5a = 5 -y = 1 y = - 1 
y = -1 --> x = 2 - 4y x = 2 - 4(-1) x = 2 - -4 x = 2 + 4 x = 6 Você resolveu o sistema de equações usando substituição. (x, y) = (6, -1) 
Preencha (6, -1) para (x, y) na equação 2x + 3y = 9. 2(6) + 3(-1) = 9 12 - 3 = 9 9 = 9 Preencha (6, -1) para (x, y) na equação x + 4y = 2. 6 + 4(-1) = 2 6 - 4 = 2 2 = 2
Resolvendo um sistema de equações
Contente
Resolver um sistema de equações requer encontrar o valor de várias variáveis em várias equações. Você pode resolver um sistema de equações usando adição, subtração, multiplicação ou substituição. Se você quiser aprender a resolver um sistema de equações, tudo o que você precisa fazer é seguir estes passos.
Degraus
Método 1 de 4: Resolva por Subtração

1. Escreva uma equação sobre a outra. Resolver essas equações com subtração é um método ideal se você ver que ambas as equações têm a mesma variável com o mesmo coeficiente e sinal. Por exemplo, se ambas as equações tiverem a variável -2x, você pode usar a subtração para encontrar o valor de ambas as variáveis.
- Escreva uma equação acima da outra de modo que as variáveis x e y de ambas as equações e os números fiquem abaixo um do outro. Coloque o sinal de menos ao lado do número inferior.
- Por exemplo: Se você tiver as duas equações a seguir: 2x + 4y = 8 e 2x + 2y = 2, ficaria assim:
- 2x + 4a = 8
- -(2x + 2y = 2)

2. Subtrair termos semelhantes. Agora que as duas equações estão alinhadas, tudo o que você precisa fazer é subtrair os termos semelhantes. Faça isso com um termo de cada vez:

3. Resolva para o prazo restante. Remova qualquer zero da equação que foi criada, isso não altera o valor e resolva a equação restante.

4. Insira o valor encontrado da variável em uma das equações. Agora que você sabe que y = 3, você pode colocar esse valor na equação original para resolver x. Não importa qual equação você escolha, a resposta é a mesma. Então use a equação mais simples!

5. Verifique sua resposta. Para certificar-se de que sua resposta está correta, insira as duas respostas em ambas as equações. Veja como fazer isso:
Método 2 de 4: Resolva por adição

1. Escreva uma equação sobre a outra. Resolver um sistema de equações por adição é o melhor método, se você notar que ambas as equações têm uma variável com o mesmo coeficiente, mas com um sinal diferente; por exemplo, se uma equação contém a variável 3x e a outra a variável -3x.
- Escreva uma equação acima da outra de modo que as variáveis x e y de ambas as equações e os números fiquem abaixo um do outro. Coloque o sinal de mais ao lado do número inferior.
- Por exemplo: Você tem as duas equações a seguir 3x + 6y = 8 e x - 6y = 4, então escreva a primeira equação acima da segunda como mostrado abaixo:
- 3x + 6a = 8
- +(x - 6y = 4)

2. Adicione termos semelhantes juntos. Agora que as duas equações estão alinhadas uma sobre a outra, tudo o que você precisa fazer é somar os termos com a mesma variável:

3. Resolva para o prazo restante. Remova qualquer zero da equação que surgiu, isso não altera o valor. Resolva a equação restante.

4. Insira o valor encontrado desta variável em uma das equações. Agora que você sabe que x = 3, você pode colocar esse valor na equação original para resolver y. Não importa qual equação você escolha, a resposta é a mesma. Então use a equação mais simples!

5. Verifique sua resposta. Para certificar-se de que sua resposta está correta, insira as duas respostas em ambas as equações. Veja como fazer isso:
Método 3 de 4: Resolva por Multiplicação

1. Escreva uma equação sobre a outra. Escreva uma equação acima da outra de modo que as variáveis x e y de ambas as equações e os números fiquem abaixo um do outro. Se você está usando multiplicação, você está fazendo isso porque nenhuma das variáveis tem coeficientes iguais - agora.
- 3x + 2a = 10
- 2x - y = 2

2. Garanta coeficientes iguais. Em seguida, multiplique uma ou ambas as equações por um número, de modo que uma das variáveis tenha o mesmo coeficiente. Nesse caso, você pode multiplicar toda a segunda equação por 2 para que -y seja igual a -2y e, portanto, o primeiro coeficiente y. Veja como fazer isso:

3. Adicionar ou subtrair as equações. Agora tudo o que você precisa fazer é eliminar termos iguais adicionando ou subtraindo. Como você está lidando com 2y e -2y aqui, faz sentido usar o método de adição porque é igual a 0. Se você estiver lidando com 2y + 2y, use o método de subtração. Aqui está um exemplo de como usar o método de adição para eliminar variáveis:

4. Resolva isso para o prazo restante. Isso é facilmente resolvido encontrando o valor do termo que você ainda não eliminou. Se 7x = 14, então x = 2.

5. Insira o valor encontrado em uma das equações. Insira o termo em uma das equações originais para resolver o outro termo. Escolha a equação mais simples para isso, esta é a mais rápida.

6. Verifique sua resposta. Para certificar-se de que sua resposta está correta, insira as duas respostas em ambas as equações. Veja como fazer isso:
Método 4 de 4: Resolva por substituição

1. Isolar uma variável. A substituição é ideal quando um dos coeficientes em uma das equações é igual a 1. Então tudo o que você precisa fazer é isolar essa variável em um lado da equação para encontrar seu valor.
- Se você está trabalhando com as equações 2x + 3y = 9 e x + 4y = 2, então você tem que isolar x na segunda equação.
- x + 4y = 2
- x = 2 - 4y

2. Preencha o valor da variável que você isolou na outra equação. Pegue o valor da variável isolada e coloque na outra equação. Claro que não na mesma equação senão você não vai resolver nada. Aqui está um exemplo de como fazer isso:

3. Resolva para a variável restante. Agora que você sabe que y = - 1, insira esse valor na equação mais simples para encontrar o valor de x. Aqui está um exemplo de como fazer isso:

4. Verifique sua resposta. Para certificar-se de que sua resposta está correta, insira as duas respostas em ambas as equações. Veja como fazer isso:
Pontas
- Agora você deve ser capaz de resolver qualquer sistema linear de equações usando adição, subtração, multiplicação ou substituição, mas um método geralmente é o mais adequado, dependendo das equações.
Artigos sobre o tópico "Resolvendo um sistema de equações"
Оцените, пожалуйста статью
Popular