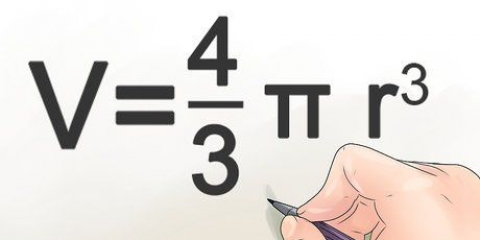Como Calcular o Volume de uma Pirâmide: 8 Passos (com Imagens)

Contente

Degraus
- Método 1 de 2: Pirâmide com base retangular
- Método 2 de 2: Pirâmide com base triangular
Pontas
Avisos

Para calcular o volume de uma pirâmide, multiplique a área da base pela altura da pirâmide. Divida o resultado por 3, isso é tudo! Leia este artigo com métodos de cálculo para uma pirâmide com base retangular e uma pirâmide com base triangular.

Degraus

Método 1 de 2: Pirâmide com base retangular

Imagem intitulada Calcular o Volume de uma Pirâmide Passo 1

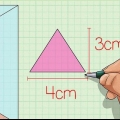
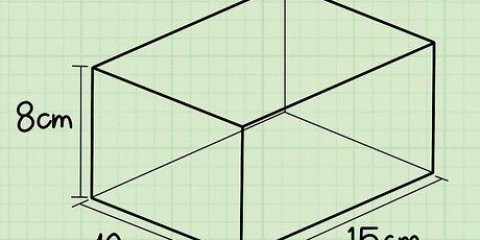
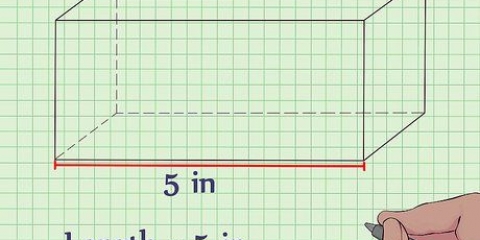
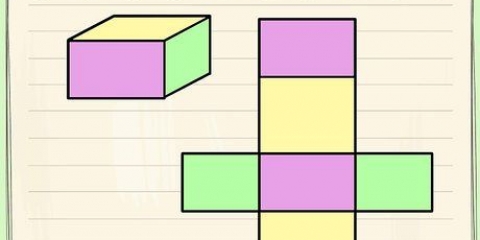
1. Determine o comprimento e a largura da base. Neste exemplo, o comprimento é 4 cm e a largura é 3 cm. Se você tem uma base quadrada, o método é o mesmo, apenas o comprimento e a largura são iguais. Anote suas medidas.

Imagem intitulada Calcular o Volume de uma Pirâmide Passo 2

2. Multiplique o comprimento pela largura para calcular a área da base. Para calcular a área do nosso exemplo, multiplicamos 3 cm por 4 cm. 3cm x 4cm = 12cm

Imagem intitulada Calcular o Volume de uma Pirâmide Passo 3

3. Multiplique a área da base pela altura. A área da base é 12 cm e a altura é 4 cm, então multiplicamos 12 cm por 4 cm. 12 cm x 4 cm = 48 cm

Imagem intitulada Calcular o Volume de uma Pirâmide Passo 4

4. Divida o resultado por 3. Isso é o mesmo que multiplicar por 1/3. 48 cm/3 = 16 cm. O volume de uma pirâmide com 4 cm de altura e base retangular com 3 cm de largura e 4 cm de comprimento é, portanto, 16 cm. Não se esqueça de indicar o resultado em unidades cúbicas.

Método 2 de 2: Pirâmide com base triangular

Imagem intitulada Calcular o Volume de uma Pirâmide Passo 5

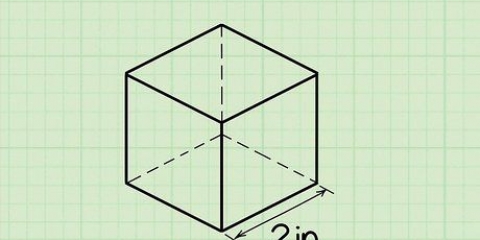
1. Determine o comprimento e a largura da base. O comprimento e a largura da base devo perpendiculares entre si, caso contrário, este método não funcionará. Eles também podem ser vistos como a parte inferior e a altura do triângulo. Neste exemplo, a largura do triângulo é 2 cm e o comprimento é 4 cm. Escreva isso.

Imagem intitulada Calcular o Volume de uma Pirâmide Passo 6

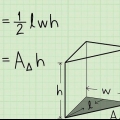
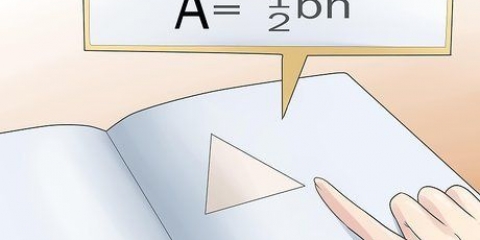
2. Calcule a área da base. Para calcular a área da base usamos a seguinte fórmula:A = 1/2(o)(h). É assim que nós fazemos:

A = 1/2(o)(h)

A = 1/2(2)(4)

A = 1/2(8)

A = 4cm

Imagem intitulada Calcular o Volume de uma Pirâmide Passo 7

3. Multiplique a área da base pela altura da pirâmide. A área da base é 4 cm e a altura é 5 cm. 4cm x 5cm = 20cm.

Imagem intitulada Calcular o Volume de uma Pirâmide Passo 8

4. Divida o resultado por 3. 20 cm/3 = 6,67 cm. O volume de uma pirâmide com 5 cm de altura e base triangular com 2 cm de largura e 4 cm de comprimento é, portanto, 6,67 cm.

Pontas

Em uma pirâmide com base quadrada, a altura, a linha que divide o lado triangular em dois triângulos iguais e a largura da base são conectadas pelo teorema de Pitágoras: (largura ÷ 2) + (altura) = (altura do triângulo)
Este método também pode ser aplicado a objetos como pirâmides pentagonais, pirâmides hexagonais, etc. O processo geral é: A) calcular a área da base; B) medir a altura do topo da pirâmide até o centro da base; C) multiplicar A por B; D) dividir por 3.
Em tudo comum pirâmides são as costelas verticais, a linha que divide o lado triangular em dois triângulos iguais e a largura da base conectada pelo teorema de Pitágoras: (comprimento do lado ÷ 2) + (comprimento da costela) = (altura)

Avisos

As pirâmides têm três tipos de alturas: a linha que divide a face triangular em dois triângulos iguais, o comprimento da costela (ao longo do lado de uma face triangular) e a altura real (da ponta da pirâmide perpendicular à base) .).