Como Calcular o Volume de uma Pirâmide Quadrada

Contente

Degraus
Pontas

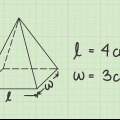
Uma pirâmide quadrada é uma figura tridimensional com uma base quadrada e inclinações triangulares que se encontram em um ponto acima da base. No evento que $s$ $s$ é o comprimento de um dos lados do quadrado e $h$ $h$ a altura da pirâmide (a distância perpendicular da base a esse ponto), então o volume de uma pirâmide quadrada pode ser calculado usando a fórmula $V = \frac{1}{3} s^{2} h$ $V={frac{1}{3}}s^{2}h$ . Não importa se a pirâmide é do tamanho de um peso de papel ou maior que a Pirâmide de Gizé - esta fórmula funciona para qualquer pirâmide quadrada. O volume também pode ser calculado usando o `apothema` da pirâmide.

Degraus

Método 1 de 3: Determine o volume com a área da base e a altura

Imagem intitulada Calcular o Volume de uma Pirâmide Quadrada Etapa 01

1. Meça o comprimento do lado da base. Como as pirâmides quadradas, por definição, têm uma base quadrada, todos os lados da base devem ter o mesmo comprimento. Então, com uma pirâmide quadrada, você só precisa saber o comprimento de um dos lados.

Suponha que você tenha uma pirâmide com uma base quadrada cujos lados têm um comprimento de $s = 5 cm$ $s=5{text{cm}}$ . Você usará esse valor para calcular a área da base.
Se os lados da base não são iguais em comprimento, então você tem um pirâmide retangular em vez de uma pirâmide quadrada. A fórmula para o volume de uma pirâmide retangular é muito semelhante à fórmula para pirâmides quadradas. No evento que $eu$ $eu$ é o comprimento da base da pirâmide retangular e $C$ $C$ a largura, então o volume da pirâmide $V = \frac{1}{3} h * eu * C$ $V={frac{1}{3}}h*l*w$ .

Imagem intitulada Calcular o Volume de uma Pirâmide Quadrada Etapa 02

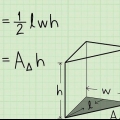
2. Calcule a área da base. Para determinar o volume, primeiro você precisa da área da base. Você faz isso multiplicando o comprimento e a largura da base. Como a base de uma pirâmide quadrada é um quadrado, todos os lados têm o mesmo comprimento e a área da base é igual ao quadrado do comprimento de um de seus lados (multiplicado por ele mesmo).

No exemplo, os lados da base da pirâmide são todos de 5 cm, e você calcula a área da base da seguinte forma:

Superfície = s^{2} = (5 cm)^{2} = 25 {cm}^{2}

${text{Area}}=s^{2}=(5{text{cm}})^{2}=25{text{cm}}^{2}$

Lembre-se que as áreas bidimensionais são expressas em quadrados – centímetros quadrados, metros, quilômetros, etc.

Imagem intitulada Calcular o Volume de uma Pirâmide Quadrada Etapa 03

3. Multiplique a área da base pela altura da pirâmide. Então você multiplica a área da base pela altura da pirâmide. Como lembrete, a altura é a distância é o comprimento do segmento de linha do topo da pirâmide até a base, em ângulos retos.

No exemplo, assumimos que a pirâmide tem uma altura de 9 cm. Nesse caso, multiplique a área da base por esse valor, da seguinte forma:

25 cm 2 * 9 cm = 225 {cm}^{3}

$25{text{cm}}^{2}*9{text{cm}}=225{text{cm}}^{3}$

Lembre-se que os volumes são expressos em unidades cúbicas. Neste caso, como todas as medidas lineares são centímetros, o volume é indicado em centímetros cúbicos.

Imagem intitulada Calcular o Volume de uma Pirâmide Quadrada Etapa 04

4. Divida esta resposta por 3. Por fim, você determina o volume da pirâmide dividindo o valor que acabou de encontrar (multiplicando a área da base pela altura) por 3. Isso calcula o volume da pirâmide quadrada.

No exemplo, divida 225 cm por 3 e a resposta é 75 cm para o volume.

Método 2 de 3: Determine o volume com o apótema

Imagem intitulada Calcular o Volume de uma Pirâmide Quadrada Etapa 05

1. Meça o apótema da pirâmide. Às vezes a altura perpendicular da pirâmide não é dada (ou você tem que medi-la), mas o apótema. Com o apótema você pode usar o teorema de Pitágoras use para calcular a altura perpendicular.

O apótema de uma pirâmide é a distância do vértice ao centro de um dos lados de sua base. Meça no centro de um dos lados e não em um dos cantos da base. Para este exemplo, assumimos que apótema é 13 cm e o comprimento de um lado da base é 10 cm.
Lembre-se que o Teorema de Pitágoras pode ser expresso como a equação $uma 2 + b^{2} = c^{2}$ $a^{2}+b^{2}=c^{2}$ , através do qual $uma$ $uma$ e $b$ $b$ os catetos perpendiculares são do triângulo retângulo e $c$ $c$ a hipotenusa.

Imagem intitulada Calcular o Volume de uma Pirâmide Quadrada Etapa 06

2. Imagine um triângulo retângulo. Para usar o teorema de Pitágoras você precisa de um triângulo retângulo. Imagine um triângulo dividindo a pirâmide ao meio e perpendicular à base da pirâmide. O apótema da pirâmide, chamado

eu

$eu$ , é a hipotenusa desse triângulo retângulo. A base desse triângulo retângulo tem metade do comprimento de

s

$s$ , o lado da base quadrada da pirâmide.

Imagem intitulada Calcular o Volume de uma Pirâmide Quadrada Etapa 07

3. Atribuir variáveis aos valores. O Teorema de Pitágoras usa as variáveis a, b e c, mas é útil substituí-las por variáveis que sejam significativas para o seu problema. o apótema

eu

$eu$ toma o lugar de

c

$c$ no teorema de Pitágoras. A perna do triângulo retângulo (

\frac{s}{2}

${frac{s}{2}}$ ), toma o lugar de

b .

$b$ Você vai a altura

h

$h$ determinar a pirâmide, que ocupa o lugar de

uma

$uma$ no teorema de Pitágoras.

Essa substituição fica assim:

uma 2 + b^{2} = c^{2}

$a^{2}+b^{2}=c^{2}$

h 2 + (\frac{s}{2})^{2} = {eu}^{2}

$h^{2}+({frac{s}{2}})^{2}=l^{2}$

Imagem intitulada Calcular o Volume de uma Pirâmide Quadrada Etapa 08

4. Use o Teorema de Pitágoras para calcular a altura perpendicular. Use os valores medidos

s = 10

$s=10$ e

eu = 13

$l=13$ . Então resolva a equação:

h 2 = {eu}^{2} - (\frac{s}{2})^{2}

$h^{2}=l^{2}-({frac{s}{2}})^{2}$ .....(equação original)

h = \sqrt{eu} 2 - (\frac{s}{2})^{2}

$h={sqrt{l^{2}-({frac{s}{2}})^{2}}}$ .....(quadrado os dois lados)

h = \sqrt{13} 2 - (\frac{10}{2})^{2}

$h={sqrt{13^{2}-({frac{10}{2}})^{2}}}$ .....(insira os valores)

h = \sqrt{169 - 5} 2

$h={sqrt{169-5^{2}}}$ .....(fração simplificada)

h = \sqrt{169 - 25}

$h={sqrt{169-25}}$ .....(simplifique quadrado)

h = \sqrt{144}

$h={sqrt{144}}$ .....(subtrair)

h = 12

$h=12$ .....(simplificar raiz)

Imagem intitulada Calcular o Volume de uma Pirâmide Quadrada Etapa 09

5. Use altura e base para calcular o volume. Depois de aplicar esses cálculos ao Teorema de Pitágoras, agora você tem as informações necessárias para calcular o volume da pirâmide. Use a fórmula

V = \frac{1}{3} s^{2} h

$V={frac{1}{3}}s^{2}h$ e resolva-os, certificando-se de dar a resposta em unidades quadradas.

Dos cálculos deduzimos que a altura da pirâmide é de 12 cm. Use isso junto com o lado de 10 cm da base para calcular o volume da pirâmide:

V = \frac{1}{3} s^{2} h

$V={frac{1}{3}}s^{2}h$

V = \frac{1}{3} (10^{2}) 12

$V={frac{1}{3}}(10^{2})12$

V = \frac{1}{3} (100) (12)

$V={frac{1}{3}}(100)(12)$

V = 400 cm 3

$V=400{text{cm}}^{3}$

Método 3 de 3: Determinando o volume com a altura das pernas

Imagem intitulada Calcular o Volume de uma Pirâmide Quadrada Passo 10

1. Meça a altura das pernas da pirâmide. A altura das pernas é o comprimento das bordas da pirâmide, medida do topo até um dos cantos da base. Como acima, use o Teorema de Pitágoras para calcular a altura perpendicular da pirâmide.

Neste exemplo, assumimos que a altura das pernas é de 11 cm e que a altura perpendicular é de 5 cm.

Imagem intitulada Calcular o Volume de uma Pirâmide Quadrada Passo 11

2. Imagine um triângulo retângulo. Novamente você precisa de um triângulo retângulo para poder usar o Teorema de Pitágoras. Neste caso, no entanto, o valor desconhecido é a base da pirâmide. Conhecida é a altura vertical e a altura das pernas. Agora imagine que você corta a pirâmide diagonalmente de um canto ao outro canto e, em seguida, abre a figura, o plano resultante se parecerá com um triângulo. A altura desse triângulo é a altura perpendicular da pirâmide. Isso divide o triângulo exposto em dois triângulos retângulos simétricos. A hipotenusa de cada um dos triângulos retângulos é a altura dos catetos da pirâmide. A base de cada um dos triângulos retângulos é metade da diagonal da base da pirâmide.

Imagem intitulada Calcular o Volume de uma Pirâmide Quadrada Passo 12

3. Atribuir variáveis. Use o triângulo retângulo imaginário e atribua valores ao Teorema de Pitágoras. Você sabe a altura vertical,

h,

$h,$ que é um lado do teorema de Pitágoras,

uma

$uma$ . A altura das pernas da pirâmide,

eu,

$eu,$ forma a hipotenusa deste triângulo retângulo imaginário e, portanto, toma o lugar de

c

$c$ . A diagonal desconhecida da base da pirâmide é o lado restante do triângulo retângulo,

b .

$b$ Depois de fazer essas substituições, a equação fica assim:

uma 2 + b^{2} = c^{2}

$a^{2}+b^{2}=c^{2}$

h 2 + b^{2} = {eu}^{2}

$h^{2}+b^{2}=l^{2}$

Imagem intitulada Calcular o Volume de uma Pirâmide Quadrada Passo 13

4. Calcule a diagonal da base quadrada. Você tem que reordenar a equação para obter a variável

b

$b$ isolar e, em seguida, calcular seu valor.

h 2 + b^{2} = {eu}^{2}

$h^{2}+b^{2}=l^{2}$ ..........(equação ajustada)

b 2 = {eu}^{2} - h^{2}

$b^{2}=l^{2}-h^{2}$ ..........(substitua h em ambos os lados)

b = \sqrt{eu} 2 - h^{2}

$b={sqrt{l^{2}-h^{2}}}$ ..........(subtrair a raiz quadrada de ambos os lados)

b = \sqrt{11} 2 - 5^{2}

$b={sqrt{11^{2}-5^{2}}}$ ..........(preencha os números)

b = \sqrt{121 - 25}

$b={sqrt{121-25}}$ ..........(simplifique os quadrados)

b = \sqrt{96}

$b={sqrt{96}}$ ..........(subtrair valores)

b = 9.80

$b=9,80$ ..........(simplifique a raiz quadrada)

Dobre este valor para encontrar a diagonal da base quadrada da pirâmide. Assim, a diagonal da base da pirâmide é 9,8 * 2 = 19,6 cm.

Imagem intitulada Calcular o Volume de uma Pirâmide Quadrada Etapa 14

5. Encontre o lado da base da diagonal. A base da pirâmide é um quadrado. A diagonal de cada quadrado é igual ao comprimento de um de seus lados, vezes a raiz quadrada de 2. E assim você pode encontrar o lado de um quadrado dividindo a diagonal pela raiz quadrada de 2.

Neste exemplo de pirâmide, a diagonal da base é 19,6 cm. Portanto, o lado é igual a: