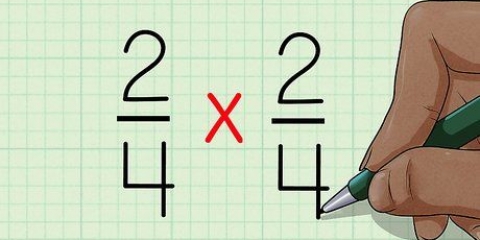Ex. 1: √(18) x √(2) = √(36) Ex. 2: √(10) x √(5) = √(50) Ex. 3: √(3) x √(9) = √(27) 
Ex. 1: √(36) = 6. 36 é um quadrado porque é um produto de 6 x 6. A raiz quadrada de 36 é apenas 6. Ex. 2: √(50) = √(25 x 2) = √([5 x 5] x 2) = 5√(2). Enquanto 50 não é um número quadrado, 25 é um fator de 50 (porque cabe exatamente duas vezes) e é um quadrado perfeito. Você pode fatorar 25 (5 x 5) e colocar um 5 fora do radical para simplificar a equação. Você pode pensar assim: se você colocar o 5 de volta no radical, ele se multiplicará por si mesmo e se tornará 25 novamente. Ex. 3:√(27) = 3. 27 a é um cubo perfeito (terceira potência), porque é o produto de 3 x 3 x 3. A raiz quadrada de 27 é, portanto, 3. 

Ex. 1: 3√(2) x √(10) = 3√(2 x 10) = 3√(20) Ex. 2: 4√(3) x 3√(6) = 12√(3 x 6) = 12√(18) 
3√(20) = 3√(4 x 5) = 3√([2 x 2] x 5) = (3 x 2)√(5) = 6√(5) 12√(18) = 12√(9 x 2) = 12√(3 x 3 x 2) = (12 x 3)√(2) = 36√(2) 

√(5) x √(2) = ? 

--> √(5) = √(5) --> √(2) = √(2) 
√(5) = √(5 x 5) = √25 √(2) = √(2 x 2 x 2) = √8 

Multiplicar números de cenoura juntos
Contente
O símbolo da raiz (√) representa a raiz quadrada de um número. Você pode encontrar o símbolo da raiz na matemática, ou mesmo na carpintaria ou em qualquer outro campo em que a geometria entre em jogo ou ao calcular dimensões ou distâncias relativas. Você pode multiplicar raízes que têm a mesma potência (raízes da potência). Se os radicais não tiverem o mesmo poder, você pode editar sua equação até que eles tenham. Se você quiser saber como multiplicar raízes com ou sem coeficientes, siga os passos abaixo.
Degraus
Método 1 de 3: Multiplicando raízes sem coeficientes

1. Certifique-se de que as raízes tenham o mesmo poder. Para multiplicar raízes usando o método básico, elas devem ter a mesma potência. O `poder` é o pequeno número escrito à esquerda da linha superior do símbolo da raiz. Se nenhuma potência for especificada, você está lidando com uma raiz quadrada (segunda potência) e pode ser multiplicada por outras raízes quadradas. Você pode multiplicar raízes de diferentes potências juntas, mas esse é um método avançado e será explicado mais tarde. Aqui estão dois exemplos de multiplicação de raízes com as mesmas potências:
- Ex. 1: √(18) x √(2) = ?
- Ex. 2: √(10) x √(5) = ?
- Ex. 3: √(3) x √(9) = ?

2. Multiplique os números sob o radical. Então você multiplica os números sob o sinal do radical e deixa lá. Isso fica assim:

3. Simplifique as raízes. Depois de multiplicar as raízes, há uma boa chance de que elas possam ser simplificadas para um quadrado perfeito ou potência de dois, ou podem ser simplificadas encontrando um quadrado como um fator do produto final. Você faz isso da seguinte forma:
Método 2 de 3: Multiplicando raízes por coeficientes

1. Multiplique os coeficientes. Os coeficientes são os números fora do radical. Se nenhum coeficiente for fornecido, você pode considerar o coeficiente como 1. Multiplique os coeficientes. Você faz isso da seguinte forma: Ex. 2: 4√(3) x 3√(6) = 12√( ? ) 4 x 3 = 12
- Ex. 1: 3√(2) x √(10) = 3√( ? )
- 3 x 1 = 3

2. Multiplique os números dentro das raízes. Depois de multiplicar os coeficientes, você pode começar a multiplicar os números dentro das raízes. Você faz isso da seguinte forma:

3. Simplifique o produto. Então você simplifica os números sob as raízes procurando os quadrados perfeitos ou múltiplos dos números sob as raízes que formam quadrados perfeitos. Depois de simplificar esses termos, multiplique seus coeficientes correspondentes por. Você faz isso da seguinte forma:
Método 3 de 3: Multiplique diferentes raízes de poder

1. Encontre o LCF (Mínimo Múltiplo Comum) das potências. Para encontrar o LCF das potências, encontre o menor número divisível por ambas as potências. Encontre o LCF dos índices para a seguinte equação: √(5) x √(2) = ?
- Os índices são 3 e 2. 6 é o LCF desses dois números, porque é o menor número divisível por 3 e 2. 6/3 = 2 e 6/2 = 3. Para multiplicar as raízes, ambas as potências devem ser 6.

2. Escreva cada expressão com o novo LCF como a potência. As expressões ficarão assim quando comparadas com seus novos poderes:

3. Encontre o número pelo qual você deve multiplicar cada uma das potências originais para determinar o LCF. Com a expressão √(5) sua potência de 3 terá que ser multiplicada por 2 para obter 6. Com a expressão √(2) você terá que multiplicar a potência 2 por 3 para obter 6.

4. Faça deste número o expoente do número dentro da raiz quadrada. Na primeira equação, 2 se torna a potência de 5. Na segunda equação, 3 se torna a potência de 2. Isso ficará assim:

5. Multiplique os números dentro das raízes por seus expoentes. Você faz isso da seguinte forma:

6. Coloque esses números sob um radical. Coloque-os sob um sinal de radical e conecte-os com um sinal de multiplicação. Este é o resultado: √(8 x 25)

7. Multiplicar. √(8 x 25) = √(200). Esta é a resposta final. Em alguns casos, você pode simplificar ainda mais essas expressões - por exemplo, se você encontrar um número que multiplicado seis vezes por si mesmo produz 200. Mas isso não é possível, o que significa que a expressão não pode ser mais simplificada.
Pontas
- Se houver um sinal de mais ou menos entre um número e o radical, então não é um coeficiente - nesse caso é um termo separado e deve ser tratado separadamente do radical. Se um radical e outro termo estão entre parênteses -- por exemplo, (2 + √5), então você deve tratar 2 e √5 separadamente ao realizar operações dentro dos parênteses, mas ao realizar operações fora dos parênteses, você tem que considere (2 + √5) como um todo.
- Sinais de raiz são outra maneira de expressar expoentes fracionários. Em outras palavras, a raiz quadrada de um número é a mesma daquele número elevado à potência de 1/2, a raiz cúbica de qualquer número é a mesma daquele número elevado à potência de 1/3 e assim por diante.
- UMA "coeficiente" é o número (se houver um número) imediatamente antes do radical. Então na expressão 2√5, 5 está abaixo do radical e o número 2 (fora do radical) é o coeficiente. Quando uma raiz e um coeficiente são representados como um grupo, isso significa que a raiz e o coeficiente devem ser multiplicados um pelo outro, como no exemplo: 2 * √5.
Artigos sobre o tópico "Multiplicar números de cenoura juntos"
Оцените, пожалуйста статью
Popular