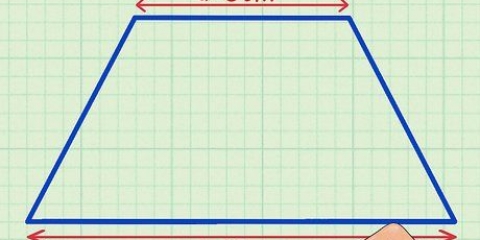
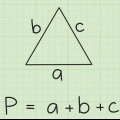Por exemplo, se você tem um trapézio com um topo de 2 cm, um fundo de 3 cm e dois lados de 1 cm, sua fórmula ficaria assim:


Por exemplo:


A circunferência do trapézio é, portanto, 7 cm. 

Por exemplo, se você tem um trapézio com uma altura de 6 cm, você precisa desenhar uma linha de cada vértice superior até o inferior. Observe 6 cm para cada linha. 
Por exemplo, se o topo do trapézio tem 6 cm, então a parte do meio do fundo também tem 6 cm. 

Por exemplo, se você sabe que a altura do trapézio é 6 cm e o comprimento do lado (hipotenusa) é 9 cm, sua equação ficaria assim:


Por exemplo: é a equação  , então você eleva 6 e 9 ao quadrado e subtrai o quadrado de 6 do quadrado de 9:
, então você eleva 6 e 9 ao quadrado e subtrai o quadrado de 6 do quadrado de 9:




Por exemplo:




Então tome nota como base do primeiro triângulo.
como base do primeiro triângulo. 
Por exemplo, se o segundo lado do trapézio for 7 cm, calcule da seguinte forma:





Então tome nota como a base do segundo triângulo.
como a base do segundo triângulo. 
Por exemplo: 
Depois de converter as raízes quadradas em decimais, você tem
Então, a circunferência aproximada do seu trapézio é 38,314 cm.. 

Por exemplo, se você tiver um trapézio com 6 cm de altura, desenhe uma linha de cada vértice superior até o inferior. Observe 6 cm em cada linha. 
Por exemplo, se o topo do trapézio tem 6 cm, então a parte do meio do fundo também tem 6 cm. 
Com esta razão você pode encontrar o comprimento da hipotenusa do triângulo, que também é o primeiro lado do trapézio. A hipotenusa é o lado oposto ao ângulo de 90 graus de um triângulo retângulo. 
Suponha que o ângulo interno dado seja de 35 graus e a altura do triângulo seja de 6 cm, então sua fórmula ficará assim:


Por exemplo, usando uma calculadora, você descobrirá que o seno de um ângulo de 35 graus é 0,5738 (arredondado). Então sua fórmula agora é:


Por exemplo:




Assim, o comprimento da hipotenusa e o primeiro lado ausente do trapézio é de cerca de 10,4566 cm. 
Por exemplo, se o ângulo interno dado for 45 graus, calcule:





Assim, o comprimento da hipotenusa e o segundo lado que falta do trapézio é de cerca de 8,4854 cm. 

Por exemplo, se o primeiro triângulo retângulo tem uma hipotenusa de 10,4566 e uma altura de 6, sua fórmula é:


Por exemplo:






Então a base do triângulo e a primeira parte que falta na base do trapézio tem cerca de 8,5639 cm. 
Por exemplo, se o segundo triângulo retângulo tiver uma hipotenusa de 8,4854 e uma altura de 6, você calcularia da seguinte forma:






Portanto, a base do segundo triângulo e a segunda parte que falta na base do trapézio é igual a 6 cm. 
Por exemplo: 
Então a circunferência aproximada do trapézio é 45,5059 cm.
Calculando o perímetro de um trapézio
Contente
Um trapézio é definido como um quadrilátero com dois lados paralelos. Como em qualquer polígono, você precisa somar todos os quatro lados para encontrar o perímetro de um trapézio (ou trapézio). Muitas vezes, no entanto, você perderá os comprimentos dos lados, mas terá outros dados, como a altura do trapézio ou as medidas dos ângulos. Usando esses dados, você pode encontrar os comprimentos desconhecidos dos lados usando as regras de geometria e trigonometria.
Degraus
Método 1 de 3: Se você souber o comprimento de ambos os lados e a base

1. Defina a fórmula para a circunferência de um trapézio. A fórmula é  , através do qual
, através do qual  é igual ao perímetro do trapézio, e a variável
é igual ao perímetro do trapézio, e a variável  é igual ao comprimento do topo do trapézio,
é igual ao comprimento do topo do trapézio,  é igual ao comprimento do fundo,
é igual ao comprimento do fundo,  é igual ao comprimento do lado esquerdo e
é igual ao comprimento do lado esquerdo e  é igual ao comprimento do lado direito.
é igual ao comprimento do lado direito.
 , através do qual
, através do qual  é igual ao perímetro do trapézio, e a variável
é igual ao perímetro do trapézio, e a variável  é igual ao comprimento do topo do trapézio,
é igual ao comprimento do topo do trapézio,  é igual ao comprimento do fundo,
é igual ao comprimento do fundo,  é igual ao comprimento do lado esquerdo e
é igual ao comprimento do lado esquerdo e  é igual ao comprimento do lado direito.
é igual ao comprimento do lado direito.
2. Use os comprimentos dos lados na fórmula. Se você não sabe o comprimento de todos os quatro lados do trapézio, não pode usar esta fórmula.


3. Adicione os comprimentos laterais juntos. Isso lhe dará a circunferência do seu trapézio.


A circunferência do trapézio é, portanto, 7 cm.
Método 2 de 3: Se você souber a altura, os dois comprimentos laterais e o comprimento superior

1. Divida o trapézio em um retângulo e dois triângulos retângulos. Para fazer isso, desenhe a altura de ambos os cantos superiores.
- Se você não puder formar os dois triângulos retângulos porque um lado do trapézio é perpendicular à base, certifique-se de que esse lado tenha o mesmo comprimento que a altura e divida o trapézio em um retângulo e um triângulo retângulo.

2. Dê o comprimento de cada linha de contorno. Como estes são os lados opostos de um retângulo, eles terão o mesmo comprimento.

3. Observe o comprimento da parte do meio da parte inferior. (Esta é a parte inferior do retângulo.) O comprimento será igual ao comprimento do topo (o topo do retângulo), porque os lados opostos de um retângulo têm o mesmo comprimento. Se você não souber o comprimento do topo, não poderá usar este método.

4. Monte o teorema de Pitágoras para o primeiro triângulo retângulo. A fórmula é  , através do qual
, através do qual  é o comprimento da hipotenusa do triângulo retângulo (o lado oposto ao ângulo reto),
é o comprimento da hipotenusa do triângulo retângulo (o lado oposto ao ângulo reto),  é a altura do triângulo retângulo e
é a altura do triângulo retângulo e  é o comprimento da base do triângulo.
é o comprimento da base do triângulo.
 , através do qual
, através do qual  é o comprimento da hipotenusa do triângulo retângulo (o lado oposto ao ângulo reto),
é o comprimento da hipotenusa do triângulo retângulo (o lado oposto ao ângulo reto),  é a altura do triângulo retângulo e
é a altura do triângulo retângulo e  é o comprimento da base do triângulo.
é o comprimento da base do triângulo.
5. Use os valores conhecidos do primeiro triângulo na fórmula. Certifique-se de inserir o comprimento lateral do trapézio para  . Insira a altura do trapézio para
. Insira a altura do trapézio para  .
.
 . Insira a altura do trapézio para
. Insira a altura do trapézio para  .
.

6. Quadrar os valores conhecidos na equação. Em seguida, subtraia os valores quadrados um do outro para obter  isolar.
isolar.
 isolar.
isolar. , então você eleva 6 e 9 ao quadrado e subtrai o quadrado de 6 do quadrado de 9:
, então você eleva 6 e 9 ao quadrado e subtrai o quadrado de 6 do quadrado de 9:



7. Tire a raiz quadrada para obter o valor de b  encontrar. (Para obter instruções completas sobre a simplificação de raízes quadradas, leia este artigo sobre o tema). O resultado lhe dará o valor da base faltante do seu primeiro triângulo retângulo. Escreva este comprimento na base do seu triângulo.
encontrar. (Para obter instruções completas sobre a simplificação de raízes quadradas, leia este artigo sobre o tema). O resultado lhe dará o valor da base faltante do seu primeiro triângulo retângulo. Escreva este comprimento na base do seu triângulo.
 encontrar. (Para obter instruções completas sobre a simplificação de raízes quadradas, leia este artigo sobre o tema). O resultado lhe dará o valor da base faltante do seu primeiro triângulo retângulo. Escreva este comprimento na base do seu triângulo.
encontrar. (Para obter instruções completas sobre a simplificação de raízes quadradas, leia este artigo sobre o tema). O resultado lhe dará o valor da base faltante do seu primeiro triângulo retângulo. Escreva este comprimento na base do seu triângulo.



Então tome nota
 como base do primeiro triângulo.
como base do primeiro triângulo.
8. Encontre o comprimento que falta do segundo triângulo retângulo. Para fazer isso, configure o teorema de Pitágoras para o segundo triângulo e siga os passos para encontrar o comprimento do lado que falta. Se você estiver trabalhando com um trapézio isósceles (aquele em que os dois lados não paralelos têm o mesmo comprimento), então os dois triângulos retângulos são congruentes, então o valor do primeiro triângulo é igual ao do segundo triângulo.





Então tome nota
 como a base do segundo triângulo.
como a base do segundo triângulo.
9. Some todos os comprimentos laterais do trapézio. O perímetro de qualquer polígono é a soma de todos os lados:  . Para a parte inferior, adicione o lado inferior do retângulo, mais as bases dos dois triângulos. Você provavelmente terá raízes quadradas em sua resposta. Para obter instruções completas sobre como adicionar raízes quadradas, leia o artigo sobre este tópico. Você também pode usar uma calculadora para converter as raízes quadradas em decimais.
. Para a parte inferior, adicione o lado inferior do retângulo, mais as bases dos dois triângulos. Você provavelmente terá raízes quadradas em sua resposta. Para obter instruções completas sobre como adicionar raízes quadradas, leia o artigo sobre este tópico. Você também pode usar uma calculadora para converter as raízes quadradas em decimais.
 . Para a parte inferior, adicione o lado inferior do retângulo, mais as bases dos dois triângulos. Você provavelmente terá raízes quadradas em sua resposta. Para obter instruções completas sobre como adicionar raízes quadradas, leia o artigo sobre este tópico. Você também pode usar uma calculadora para converter as raízes quadradas em decimais.
. Para a parte inferior, adicione o lado inferior do retângulo, mais as bases dos dois triângulos. Você provavelmente terá raízes quadradas em sua resposta. Para obter instruções completas sobre como adicionar raízes quadradas, leia o artigo sobre este tópico. Você também pode usar uma calculadora para converter as raízes quadradas em decimais.
Depois de converter as raízes quadradas em decimais, você tem

Então, a circunferência aproximada do seu trapézio é 38,314 cm..
Método 3 de 3: Se você souber a altura, o comprimento dos cantos internos superior e inferior

1. Divida o trapézio em um retângulo e dois triângulos retângulos. Para isso, indique a altura de ambos os cantos superiores.
- Se você não pode formar dois triângulos retângulos porque um lado do trapézio é perpendicular à base, certifique-se de que esse lado tenha o mesmo tamanho que a altura e divida o trapézio em um retângulo e um triângulo retângulo.

2. Rotule cada contorno. Como são lados opostos de um retângulo, eles terão o mesmo comprimento.

3. Observe o comprimento da parte do meio da parte inferior. (Esta é a parte inferior do retângulo.) Este comprimento será igual ao comprimento do topo, porque os lados opostos de um retângulo têm o mesmo comprimento.

4. Configure a fórmula do seno para o primeiro triângulo retângulo. A fórmula é  , através do qual
, através do qual  o canto interno é,
o canto interno é,  a altura do triângulo e
a altura do triângulo e  é o comprimento da hipotenusa.
é o comprimento da hipotenusa.
 , através do qual
, através do qual  o canto interno é,
o canto interno é,  a altura do triângulo e
a altura do triângulo e  é o comprimento da hipotenusa.
é o comprimento da hipotenusa.
5. Use os valores conhecidos na razão seno. Certifique-se de usar a altura do triângulo como o comprimento do lado oposto na fórmula. você resolve isso para H.


6. Determine o seno do ângulo. Faça isso usando o botão SIN em uma calculadora científica. Use este valor na fórmula.


7. Resolva isso para H. Para fazer isso, multiplique cada lado por H, depois divida cada lado pelo ângulo seno. Ou divida a altura do triângulo pelo ângulo seno.




Assim, o comprimento da hipotenusa e o primeiro lado ausente do trapézio é de cerca de 10,4566 cm.

8. Encontre o comprimento da hipotenusa do segundo triângulo retângulo. Defina a fórmula do seno ( ) para o segundo ângulo interno dado. Isso lhe dará o comprimento da hipotenusa, que também é o primeiro lado do trapézio.
) para o segundo ângulo interno dado. Isso lhe dará o comprimento da hipotenusa, que também é o primeiro lado do trapézio.
 ) para o segundo ângulo interno dado. Isso lhe dará o comprimento da hipotenusa, que também é o primeiro lado do trapézio.
) para o segundo ângulo interno dado. Isso lhe dará o comprimento da hipotenusa, que também é o primeiro lado do trapézio.




Assim, o comprimento da hipotenusa e o segundo lado que falta do trapézio é de cerca de 8,4854 cm.

9. Monte o teorema de Pitágoras para o primeiro triângulo retângulo. O teorema de Pitágoras é alto  , onde o comprimento da hipotenusa é igual a
, onde o comprimento da hipotenusa é igual a  , e a altura do triângulo
, e a altura do triângulo  .
.
 , onde o comprimento da hipotenusa é igual a
, onde o comprimento da hipotenusa é igual a  , e a altura do triângulo
, e a altura do triângulo  .
.
10. Use os valores conhecidos no teorema de Pitágoras para o primeiro triângulo retângulo. Certifique-se de inserir o valor correto para a hipotenusa  e a altura
e a altura  .
.
 e a altura
e a altura  .
.

11. Resolva isso para b  . Isso lhe dará o comprimento da base do primeiro triângulo retângulo e a primeira parte que falta da base do trapézio.
. Isso lhe dará o comprimento da base do primeiro triângulo retângulo e a primeira parte que falta da base do trapézio.
 . Isso lhe dará o comprimento da base do primeiro triângulo retângulo e a primeira parte que falta da base do trapézio.
. Isso lhe dará o comprimento da base do primeiro triângulo retângulo e a primeira parte que falta da base do trapézio.





Então a base do triângulo e a primeira parte que falta na base do trapézio tem cerca de 8,5639 cm.

12. Encontre o comprimento da base que falta do segundo triângulo retângulo. Use o teorema de Pitágoras ( ). Use o comprimento da hipotenusa para
). Use o comprimento da hipotenusa para  e a altura para
e a altura para  . Resolva isso para
. Resolva isso para  e você obtém o comprimento da segunda parte que falta no fundo do trapézio.
e você obtém o comprimento da segunda parte que falta no fundo do trapézio.
 ). Use o comprimento da hipotenusa para
). Use o comprimento da hipotenusa para  e a altura para
e a altura para  . Resolva isso para
. Resolva isso para  e você obtém o comprimento da segunda parte que falta no fundo do trapézio.
e você obtém o comprimento da segunda parte que falta no fundo do trapézio.





Portanto, a base do segundo triângulo e a segunda parte que falta na base do trapézio é igual a 6 cm.

13. Adicione todos os lados do trapézio juntos. O perímetro de qualquer polígono é a soma de todos os lados:  . Para a parte inferior, adicione a parte inferior do retângulo à base dos dois triângulos.
. Para a parte inferior, adicione a parte inferior do retângulo à base dos dois triângulos.
 . Para a parte inferior, adicione a parte inferior do retângulo à base dos dois triângulos.
. Para a parte inferior, adicione a parte inferior do retângulo à base dos dois triângulos.
Então a circunferência aproximada do trapézio é 45,5059 cm.
Pontas
- Use as leis dos triângulos especiais para encontrar os comprimentos ausentes de triângulos especiais, sem usar a fórmula do seno ou o teorema de Pitágoras. As leis se aplicam a um triângulo 30-60-90 ou a um triângulo 90-45-45.
- Use uma calculadora científica para determinar o seno de um ângulo, inserindo o ângulo e pressionando o botão `SIN`. Você também pode usar uma tabela de trigonometria.
Necessidades
- Calculadora
- Lápis
- Papel
Artigos sobre o tópico "Calculando o perímetro de um trapézio"
Оцените, пожалуйста статью
Similar
Popular