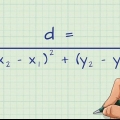Determine a distância ao longo do eixo y. Para os pontos de exemplo (3.2) e (7.8), onde o ponto 1 é (3.2) e o ponto 2 (7.8) isso se torna: (y2 - y1) = 8 - 2 = 6. Isso significa que a distância no eixo y entre esses dois pontos é de seis unidades de comprimento. Determine a distância ao longo do eixo x. Para os mesmos pontos de amostra (3.2) e (7.8): (x2 - x1) = 7 - 3 = 4. Isso significa que existem quatro unidades de comprimento separando os dois pontos no eixo x. 




Continuando com o exemplo, a distância entre (3,2) e (7,8) é a raiz quadrada de 52, ou aproximadamente 7,21.
Calcule a distância entre dois pontos
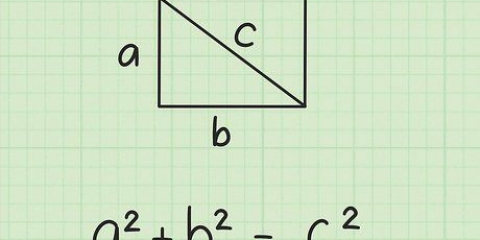
Pense na distância entre quaisquer dois pontos como uma linha. O comprimento desta linha pode ser encontrado usando a fórmula da distância: 
Degraus

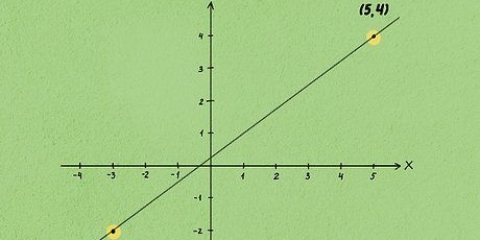
1. Pegue as coordenadas de dois pontos entre os quais você deseja encontrar a distância. Chame um ponto 1 (x1,y1) e o outro ponto 2 (x2,y2). Não importa de que ponto você começa, desde que você aplique os rótulos (1 e 2) de forma consistente ao longo do problema.
- x1 é a coordenada horizontal (ao longo do eixo x) do ponto 1, e x2 é a coordenada horizontal do ponto 2. y1 é a coordenada vertical (ao longo do eixo y) do ponto 1, e y2 é a coordenada vertical do ponto 2.
- Não, por exemplo os pontos (3.2) e (7.8). Se (3.2) é igual a (x1,y1), então (7.8) é igual a (x2,y2).

2. Use a fórmula da distância. Esta fórmula determina o comprimento de uma linha reta entre dois pontos: ponto 1 e ponto 2. A distância linear é a raiz quadrada do quadrado da distância horizontal, mais o quadrado da distância vertical entre dois pontos. Simplificando, é a raiz quadrada de: 


3. Determine a distância horizontal e vertical entre os pontos. Primeiro calcule y2 - y1 para encontrar a distância vertical. Em seguida, calcule x2 - x1 para encontrar a distância horizontal. Não se preocupe se a subtração produzir números negativos. O próximo passo é elevar ao quadrado esses valores (o que sempre resulta em um inteiro positivo).

4. Quadrar ambos os valores. Isso significa que você eleva ao quadrado a distância do eixo x (x2 - x1) e eleva ao quadrado a distância do eixo y (y2 - y1).



5. Junte os quadrados. Isso lhe dará o quadrado da diagonal, distância linear entre seus dois pontos. No exemplo dos pontos (3.2) e (7.8) o quadrado de (7 - 3) é 16, e o quadrado de (8 - 2) é 36. 36 + 16 = 52.

6. Tire a raiz quadrada da equação. Este é o último passo da equação. A distância linear entre os dois pontos é a raiz quadrada da soma dos quadrados da distância no eixo x e a distância no eixo y.
Pontas
- Não importa se você obtém um número negativo depois de subtrair y2 - y1 ou x2 - x1. Porque a diferença é ao quadrado, você sempre obtém uma distância positiva em sua resposta.
Artigos sobre o tópico "Calcule a distância entre dois pontos"
Оцените, пожалуйста статью
Similar
Popular