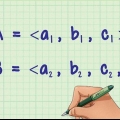Encontre o ângulo entre dois vetores

Contente

Degraus
Pontas

Matemáticos e físicos geralmente precisam encontrar o ângulo entre dois vetores dados. Embora seja fácil encontrar o ângulo entre dois vetores no mesmo plano por meio de gráficos, pode ser um pouco mais complicado no espaço ou em três dimensões. Este artigo explica o método a ser usado para encontrar o ângulo entre dois vetores no plano ou no espaço.

Degraus

Método 1 de 4: Determine os vetores

1. Determine os vetores necessários para encontrar o ângulo. Pegue os dois vetores PARA e OQ que se interceptam no ponto O e calcule o ângulo MOQ. Você deve usar os vetores PARA e OQ use, não MO ou QO. No evento que MO é conhecido, multiplique por -1 para obter PARA para obter.

Método 2 de 4: encontre o produto escalar

Encontre o produto escalar (ou produto escalar) dos dois vetores. Se você não sabe como calcular o produto escalar de dois vetores, continue lendo:

1. Determine as componentes do vetor em cada direção. Quando os vetores são listados em uma tabela, a primeira linha geralmente representa o eixo x, a segunda linha representa o eixo y e a terceira representa o eixo z. Se o vetor for escrito na forma xeu + yj + zk, Em seguida, defina os coeficientes de eu, você, e k a magnitude dos componentes ao longo dos eixos x, y e z (eu, você, e k são os vetores ao longo dos eixos x, y e z).

2. Multiplique os componentes de ambos os vetores ao longo do eixo x. Em seguida, multiplique os componentes de ambos os vetores ao longo do eixo y e faça o mesmo para os componentes ao longo do eixo z.

3. Adicione os três produtos juntos. Este é o produto escalar de ambos os vetores. O produto escalar, ou "produto interno", de dois vetores é um número muito útil em geometria e física. No momento, usamos este produto apenas como uma ferramenta para calcular o ângulo entre dois vetores. Em um vetor bidimensional, o componente ao longo do eixo z é zero, de modo que o produto escalar pode ser encontrado considerando apenas os componentes ao longo do eixo x e y.

Método 3 de 4: Calcule o tamanho

1. Calcule o módulo dos dois vetores. Calcule o módulo dos dois vetores, usando a fórmula a=b+c+d, através do qual uma é a magnitude do vetor, e b,c, e d o tamanho dos componentes nas três direções diferentes. No plano plano d ser igual a zero.