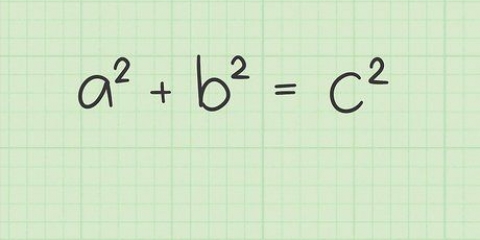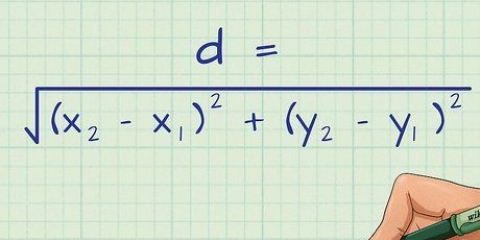Por exemplo, se a largura de um retângulo for 3 cm e o comprimento for 4 cm, sua fórmula ficaria assim:  .
. 
Por exemplo:




Por exemplo:



Então, a diagonal ou retângulo com uma largura de 3 cm e um comprimento de 4 cm é 5 cm. 

Por exemplo, se a área do retângulo for 35 centímetros quadrados, sua fórmula ficaria assim:  .
. 
Por exemplo:

 .
. 

Por exemplo, se o perímetro de um retângulo for 24 centímetros, sua fórmula ficaria assim:  .
. 
Por exemplo:


 .
. 
Por exemplo, se você encontrou com a fórmula de área que  , então você substitui o valor
, então você substitui o valor  na fórmula circunferencial:
na fórmula circunferencial:



Por exemplo:




Por exemplo:




Por exemplo,  está se tornando
está se tornando  .
. 
Por exemplo, a equação  pode ser dissolvido em
pode ser dissolvido em  .
. 
Por exemplo:


E

 .
.
Então, o comprimento e a largura do retângulo são 7 cm e 5 cm. 
Você está usando o Teorema de Pitágoras porque a diagonal de um retângulo o divide em dois triângulos retângulos congruentes. A largura e o comprimento do retângulo são os comprimentos dos lados do triângulo; a diagonal é a hipotenusa do triângulo. 
Por exemplo, se você souber que a largura e o comprimento do retângulo são 5 cm e 7 cm, sua fórmula ficaria assim:  .
. 
Por exemplo:




Por exemplo:



Portanto, a diagonal de um retângulo com área de 35 cm e perímetro de 24 cm é cerca de 8,6 cm. 

Você pode usar esse método se souber o perímetro do retângulo, exceto que agora está usando a fórmula do perímetro em vez da fórmula da área. A fórmula do perímetro de um retângulo é  , através do qual
, através do qual  é igual à largura do retângulo, e
é igual à largura do retângulo, e  é igual ao comprimento do retângulo.
é igual ao comprimento do retângulo. 
Por exemplo, se a área do retângulo for 35 centímetros quadrados, sua fórmula ficaria em volts:  .
. 
Por exemplo, se você descobriu que  , então você substitui essa relação por
, então você substitui essa relação por  na fórmula da área:
na fórmula da área:



Por exemplo:




Por exemplo, a equação  pode ser dissolvido como
pode ser dissolvido como  .
. 
Por exemplo:


E

 .
.
Neste caso, há uma resposta negativa. Como o comprimento de um retângulo não pode ser negativo, você sabe que o comprimento deve ser 5 cm. 
Por exemplo, se você sabe que o comprimento do retângulo é 5 cm e que a relação entre os comprimentos dos lados é igual a  , então você insere 5 como comprimento na fórmula:
, então você insere 5 como comprimento na fórmula:




Você usa o teorema de Pitágoras porque a diagonal de um retângulo o divide em dois triângulos retângulos congruentes. A largura e o comprimento do retângulo são os comprimentos dos lados do triângulo; a diagonal é a hipotenusa do triângulo. 
Por exemplo, se você sabe que a largura e o comprimento do retângulo são iguais a 5 cm e 7 cm, sua fórmula agora fica assim:  .
. 
Por exemplo:




Por exemplo:



Portanto, a diagonal de um retângulo com uma largura 2 cm a mais que seu comprimento e uma área de 35 cm é de cerca de 8,6 cm.
Calcule o comprimento da diagonal de um retângulo
Contente
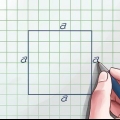
Uma diagonal é uma linha reta que liga um canto de um retângulo com o canto oposto. Um retângulo tem duas diagonais, cada uma com o mesmo comprimento. Se você conhece os comprimentos dos lados de um retângulo, é fácil encontrar o comprimento da diagonal usando o Teorema de Pitágoras, porque uma diagonal divide um retângulo em dois triângulos retângulos. Se você não conhece os comprimentos dos lados, mas tem outros dados (como a área e o perímetro, ou a razão entre os comprimentos dos lados), você pode medir o comprimento e a largura dos lados com um alguns passos extras. encontre o retângulo e, em seguida, usando o teorema de Pitágoras, encontre o comprimento e a largura da diagonal.
Degraus
Método 1 de 3: usando o comprimento e a largura

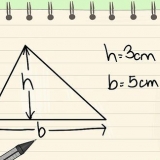
1. Escreva a fórmula do teorema de Pitágoras. A fórmula é  , através do qual
, através do qual  e
e  são iguais aos comprimentos dos lados de um triângulo retângulo, e
são iguais aos comprimentos dos lados de um triângulo retângulo, e  é igual ao comprimento da hipotenusa de um triângulo retângulo.
é igual ao comprimento da hipotenusa de um triângulo retângulo.
 , através do qual
, através do qual  e
e  são iguais aos comprimentos dos lados de um triângulo retângulo, e
são iguais aos comprimentos dos lados de um triângulo retângulo, e  é igual ao comprimento da hipotenusa de um triângulo retângulo.
é igual ao comprimento da hipotenusa de um triângulo retângulo. - Você usa o teorema de Pitágoras porque a diagonal de um retângulo o divide em dois triângulos retângulos congruentes. O comprimento e a largura do retângulo são os comprimentos dos lados do triângulo; a diagonal é a hipotenusa do triângulo.

2. Aplique o comprimento e a largura à fórmula. Estes são se for dado corretamente, ou você pode medi-los. Certifique-se de substituir por  e
e  .
.
 e
e  .
. .
.
3. Esquadre o comprimento e a largura e some esses números. Elevar ao quadrado é multiplicar o número por ele mesmo.




4. Subtraia a raiz quadrada de cada lado da equação. A maneira mais fácil de encontrar uma raiz quadrada é usar uma calculadora. Você pode usar uma calculadora online se não tiver uma calculadora científica. Isso lhe dá o valor  , ou a hipotenusa do triângulo e a diagonal do retângulo.
, ou a hipotenusa do triângulo e a diagonal do retângulo.
 , ou a hipotenusa do triângulo e a diagonal do retângulo.
, ou a hipotenusa do triângulo e a diagonal do retângulo.


Então, a diagonal ou retângulo com uma largura de 3 cm e um comprimento de 4 cm é 5 cm.
Método 2 de 3: Usando a área e o perímetro

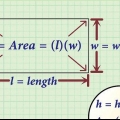
1. Escreva a fórmula da área de um retângulo. A fórmula é  , através do qual
, através do qual  é igual a área do retângulo,
é igual a área do retângulo,  é igual ao comprimento do retângulo, e
é igual ao comprimento do retângulo, e  é igual à largura do retângulo.
é igual à largura do retângulo.
 , através do qual
, através do qual  é igual a área do retângulo,
é igual a área do retângulo,  é igual ao comprimento do retângulo, e
é igual ao comprimento do retângulo, e  é igual à largura do retângulo.
é igual à largura do retângulo.
2. Use a área do retângulo na fórmula. Certifique-se de substituir a variável correta  .
.
 .
. .
.
3. Reorganize a fórmula e você obterá um valor para C  . Você faz isso dividindo ambos os lados da equação por
. Você faz isso dividindo ambos os lados da equação por  . Deixe esse valor de lado. Você usará isso mais tarde na fórmula para o perímetro.
. Deixe esse valor de lado. Você usará isso mais tarde na fórmula para o perímetro.
 . Você faz isso dividindo ambos os lados da equação por
. Você faz isso dividindo ambos os lados da equação por  . Deixe esse valor de lado. Você usará isso mais tarde na fórmula para o perímetro.
. Deixe esse valor de lado. Você usará isso mais tarde na fórmula para o perímetro.
 .
.
4. Escreva a fórmula do perímetro de um retângulo. A fórmula é  , através do qual
, através do qual  é igual à largura do retângulo, e
é igual à largura do retângulo, e  é igual ao comprimento do retângulo.
é igual ao comprimento do retângulo.
 , através do qual
, através do qual  é igual à largura do retângulo, e
é igual à largura do retângulo, e  é igual ao comprimento do retângulo.
é igual ao comprimento do retângulo.
5. Use o valor do perímetro na fórmula. Certifique-se de substituir a variável  .
.
 .
. .
.
6. Divida os dois lados da equação por 2. Isso lhe dá o valor  .
.
 .
.

 .
.
7. Usar o valor C  na equação. Use o valor encontrado reorganizando a fórmula da área.
na equação. Use o valor encontrado reorganizando a fórmula da área.
 na equação. Use o valor encontrado reorganizando a fórmula da área.
na equação. Use o valor encontrado reorganizando a fórmula da área. , então você substitui o valor
, então você substitui o valor  na fórmula circunferencial:
na fórmula circunferencial:


8. Elimine a fração da equação. Você faz isso multiplicando ambos os lados da equação por  .
.
 .
.



9. Defina a equação igual a 0. Você faz isso subtraindo o termo de primeiro grau de ambos os lados da equação.




10. Reorganizar a ordem dos termos na equação. Isso significa que o termo com o expoente vem primeiro, seguido pelo termo com a variável e, finalmente, a constante. Ao reorganizar, preste atenção aos sinais positivos e negativos corretos. A equação é agora ordenada como equação quadrática.
 está se tornando
está se tornando  .
.
11. Fatore a equação quadrática. Para obter instruções detalhadas sobre como fazer isso, leia o artigo Resolver equações quadráticas.
 pode ser dissolvido em
pode ser dissolvido em  .
.
12. Determine os valores de eu  . Você faz isso definindo cada termo como zero e resolvendo a variável. Você obtém duas soluções para esta equação. Como você está lidando com um retângulo, as duas soluções serão a largura e o comprimento do seu retângulo.
. Você faz isso definindo cada termo como zero e resolvendo a variável. Você obtém duas soluções para esta equação. Como você está lidando com um retângulo, as duas soluções serão a largura e o comprimento do seu retângulo.
 . Você faz isso definindo cada termo como zero e resolvendo a variável. Você obtém duas soluções para esta equação. Como você está lidando com um retângulo, as duas soluções serão a largura e o comprimento do seu retângulo.
. Você faz isso definindo cada termo como zero e resolvendo a variável. Você obtém duas soluções para esta equação. Como você está lidando com um retângulo, as duas soluções serão a largura e o comprimento do seu retângulo.

E

 .
.Então, o comprimento e a largura do retângulo são 7 cm e 5 cm.

13. Escreva a fórmula do teorema de Pitágoras. A fórmula é  , através do qual
, através do qual  e
e  são iguais aos comprimentos dos lados de um triângulo retângulo, e
são iguais aos comprimentos dos lados de um triângulo retângulo, e  é igual ao comprimento da hipotenusa de um triângulo retângulo.
é igual ao comprimento da hipotenusa de um triângulo retângulo.
 , através do qual
, através do qual  e
e  são iguais aos comprimentos dos lados de um triângulo retângulo, e
são iguais aos comprimentos dos lados de um triângulo retângulo, e  é igual ao comprimento da hipotenusa de um triângulo retângulo.
é igual ao comprimento da hipotenusa de um triângulo retângulo.
14. Use a latitude e longitude na fórmula. Não importa qual valor você usa para qual variável.
 .
.
15. Esquadre a latitude e a longitude e some esses números. Quadrar significa multiplicar um número por ele mesmo.




16. Tire a raiz quadrada de cada lado da equação. A maneira mais fácil de encontrar uma raiz quadrada é usando uma calculadora. Você pode usar uma calculadora online se não tiver uma calculadora científica. Isso lhe dá o valor  , e essa é a hipotenusa do triângulo e a diagonal do retângulo.
, e essa é a hipotenusa do triângulo e a diagonal do retângulo.
 , e essa é a hipotenusa do triângulo e a diagonal do retângulo.
, e essa é a hipotenusa do triângulo e a diagonal do retângulo.


Portanto, a diagonal de um retângulo com área de 35 cm e perímetro de 24 cm é cerca de 8,6 cm.
Método 3 de 3: Usando a área e os comprimentos relacionais dos lados

1. Escreva uma fórmula que explique a relação entre os comprimentos dos lados. Você pode alterar o comprimento ( ) ou a largura (
) ou a largura ( ) isolar. Deixe esta fórmula de lado por um momento. Em breve você estará usando-o na fórmula de superfície.
) isolar. Deixe esta fórmula de lado por um momento. Em breve você estará usando-o na fórmula de superfície.
 ) ou a largura (
) ou a largura ( ) isolar. Deixe esta fórmula de lado por um momento. Em breve você estará usando-o na fórmula de superfície.
) isolar. Deixe esta fórmula de lado por um momento. Em breve você estará usando-o na fórmula de superfície. - Por exemplo, se você sabe que a largura de um retângulo é 2 cm maior que seu comprimento, você pode escrever uma fórmula como
:
.

2. Escreva a fórmula da área de um retângulo. A fórmula é  , através do qual
, através do qual  é igual a área do retângulo,
é igual a área do retângulo,  é igual ao comprimento do retângulo, e
é igual ao comprimento do retângulo, e  é igual à largura do retângulo.
é igual à largura do retângulo.
 , através do qual
, através do qual  é igual a área do retângulo,
é igual a área do retângulo,  é igual ao comprimento do retângulo, e
é igual ao comprimento do retângulo, e  é igual à largura do retângulo.
é igual à largura do retângulo. , através do qual
, através do qual  é igual à largura do retângulo, e
é igual à largura do retângulo, e  é igual ao comprimento do retângulo.
é igual ao comprimento do retângulo.
3. Use a área do retângulo na fórmula. Certifique-se de substituir a variável  .
.
 .
. .
.
4. Use a fórmula relacional para o comprimento (ou largura) na fórmula. Como você está lidando com um retângulo, não importa se você está trabalhando com variável  ou
ou  .
.
 ou
ou  .
. , então você substitui essa relação por
, então você substitui essa relação por  na fórmula da área:
na fórmula da área:


5. Faça uma equação quadrática. Você faz isso usando a propriedade distributiva e multiplicando os termos entre parênteses, após o que você define a equação igual a 0.




6. Fatore a equação quadrática. Para obter instruções detalhadas sobre como fazer isso, leia o artigo Resolver equações quadráticas.
 pode ser dissolvido como
pode ser dissolvido como  .
.
7. Determine os valores de eu  . Você faz isso tornando cada termo igual a zero e resolvendo para a variável. Você encontra duas soluções para a equação.
. Você faz isso tornando cada termo igual a zero e resolvendo para a variável. Você encontra duas soluções para a equação.
 . Você faz isso tornando cada termo igual a zero e resolvendo para a variável. Você encontra duas soluções para a equação.
. Você faz isso tornando cada termo igual a zero e resolvendo para a variável. Você encontra duas soluções para a equação.

E

 .
.Neste caso, há uma resposta negativa. Como o comprimento de um retângulo não pode ser negativo, você sabe que o comprimento deve ser 5 cm.

8. Use o valor do comprimento (ou largura) em sua fórmula de relacionamento. Isso lhe dará o comprimento do outro lado do retângulo.
 , então você insere 5 como comprimento na fórmula:
, então você insere 5 como comprimento na fórmula:



9. Escreva a fórmula do teorema de Pitágoras. A fórmula é  , através do qual
, através do qual  e
e  são iguais aos comprimentos dos lados de um triângulo retângulo, e
são iguais aos comprimentos dos lados de um triângulo retângulo, e  é igual ao comprimento da hipotenusa de um triângulo retângulo.
é igual ao comprimento da hipotenusa de um triângulo retângulo.
 , através do qual
, através do qual  e
e  são iguais aos comprimentos dos lados de um triângulo retângulo, e
são iguais aos comprimentos dos lados de um triângulo retângulo, e  é igual ao comprimento da hipotenusa de um triângulo retângulo.
é igual ao comprimento da hipotenusa de um triângulo retângulo.
10. Use a latitude e longitude na fórmula. Não importa qual valor você usa para qual variável.
 .
.
11. Esquadre a latitude e a longitude e some esses números. Quadrar significa multiplicar um número por ele mesmo.




12. Subtraia a raiz quadrada de cada lado da equação. A maneira mais fácil de encontrar uma raiz quadrada é usando uma calculadora. Você pode usar uma calculadora online se não tiver uma calculadora científica. Isso lhe dá o valor  , ou a hipotenusa do triângulo e, portanto, a diagonal do retângulo.
, ou a hipotenusa do triângulo e, portanto, a diagonal do retângulo.
 , ou a hipotenusa do triângulo e, portanto, a diagonal do retângulo.
, ou a hipotenusa do triângulo e, portanto, a diagonal do retângulo.


Portanto, a diagonal de um retângulo com uma largura 2 cm a mais que seu comprimento e uma área de 35 cm é de cerca de 8,6 cm.
Artigos sobre o tópico "Calcule o comprimento da diagonal de um retângulo"
Оцените, пожалуйста статью
Popular