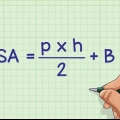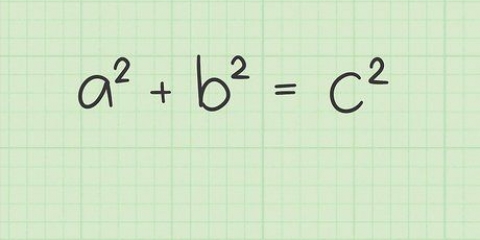Por exemplo, se você deseja encontrar a largura de um retângulo com área de 24 cm e comprimento de 8 cm, sua fórmula ficaria assim:


Por exemplo, na equação  , divida cada lado por 8.
, divida cada lado por 8.




Por exemplo, para um retângulo com área de  e um comprimento de
e um comprimento de  , torna-se a largura
, torna-se a largura  .
. 
Por exemplo, se você quisesse encontrar a largura de um retângulo com uma circunferência de 22 cm e um comprimento de 8 cm, a fórmula ficaria assim:



Por exemplo, na equação  , subtraia 16 de cada lado e divida por 2.
, subtraia 16 de cada lado e divida por 2.





Por exemplo, para um retângulo com perímetro de  e um comprimento de
e um comprimento de  , torna-se a largura
, torna-se a largura  .
. 

Por exemplo, ao determinar a largura de um retângulo com diagonal de 5 cm e lado de 4 cm, a fórmula ficaria assim: 

Por exemplo:




Por exemplo, na equação  , subtrair 16 de cada lado.
, subtrair 16 de cada lado.



Por exemplo:



Por exemplo, para um retângulo com uma diagonal de  e um lado de
e um lado de  , torna-se a largura
, torna-se a largura  .
. 

A relação pode ser dada declarando quantas vezes um lado é maior que o outro, ou quantas unidades mais ou menos. Por exemplo, pode-se saber que o comprimento é cinco centímetros maior que a largura. A expressão para o comprimento torna-se então  .
. 
Por exemplo, se você sabe que a área é 24 cm, e que  , então a fórmula fica assim:
, então a fórmula fica assim:



Por exemplo, simplifique  até
até  .
. 
Você pode precisar adicionar ou subtrair para resolver isso, ou fatorar ou usar uma equação quadrática para resolver isso. Por exemplo,  pode ser dissolvido da seguinte forma:
pode ser dissolvido da seguinte forma:


Você então tem duas soluções possíveis para :
: ou
ou  . Como um retângulo não pode ter largura negativa, você pode excluir -8. Assim é a sua solução
. Como um retângulo não pode ter largura negativa, você pode excluir -8. Assim é a sua solução  .
.
Determinando a largura de um retângulo
Contente
Existem várias maneiras de encontrar as dimensões ausentes de um retângulo, e o método usado dependerá dos dados que você possui. Desde que a área ou perímetro seja conhecido, bem como o comprimento de um lado do retângulo (ou a razão entre seu comprimento e largura), a dimensão que falta pode ser determinada. As propriedades de um retângulo são tais que esses métodos podem ser usados para determinar sua latitude ou longitude.
Degraus
Método 1 de 4: Usando a área e o comprimento

1. Anote a fórmula para a área de um retângulo. A fórmula é  , através do qual
, através do qual  é igual a área do retângulo,
é igual a área do retângulo,  é igual ao comprimento do retângulo, e
é igual ao comprimento do retângulo, e  é igual à largura do retângulo.
é igual à largura do retângulo.
 , através do qual
, através do qual  é igual a área do retângulo,
é igual a área do retângulo,  é igual ao comprimento do retângulo, e
é igual ao comprimento do retângulo, e  é igual à largura do retângulo.
é igual à largura do retângulo. - O método só funciona para uma determinada área e comprimento do retângulo.
- Esta fórmula também está disponível na forma
, através do qual
é igual à altura do retângulo (em vez do comprimento). Esses dois termos referem-se às mesmas dimensões.

2. Use os valores de área e comprimento na fórmula. Certifique-se de substituir as variáveis corretas.


3. Resolva para C  . Você faz isso dividindo cada lado da equação pelo seu comprimento.
. Você faz isso dividindo cada lado da equação pelo seu comprimento.
 . Você faz isso dividindo cada lado da equação pelo seu comprimento.
. Você faz isso dividindo cada lado da equação pelo seu comprimento. , divida cada lado por 8.
, divida cada lado por 8.



4. Anote sua resposta final. Não se esqueça de mencionar a unidade das leituras.
 e um comprimento de
e um comprimento de  , torna-se a largura
, torna-se a largura  .
.Método 2 de 4: Usando a circunferência e o comprimento
1. Escreva a fórmula do perímetro de um retângulo. A fórmula é  , através do qual
, através do qual  é igual ao perímetro do retângulo,
é igual ao perímetro do retângulo,  é igual ao comprimento do retângulo, e
é igual ao comprimento do retângulo, e  é igual à largura do retângulo.
é igual à largura do retângulo.
 , através do qual
, através do qual  é igual ao perímetro do retângulo,
é igual ao perímetro do retângulo,  é igual ao comprimento do retângulo, e
é igual ao comprimento do retângulo, e  é igual à largura do retângulo.
é igual à largura do retângulo.- Este método só funciona para um determinado perímetro e comprimento do retângulo.
- Esta fórmula também é escrita como
, através do qual
é igual à altura do retângulo e é usado em vez do comprimento. As variáveis
e
referem-se às mesmas dimensões, e a propriedade distributiva dita que essas duas fórmulas, embora ordenadas de forma diferente, produzem o mesmo resultado.

2. Use a circunferência e o comprimento na fórmula. Certifique-se de substituir as variáveis corretas.



3. Resolver C  . Para fazer isso, você precisa subtrair o comprimento de cada lado da equação e dividi-lo por 2.
. Para fazer isso, você precisa subtrair o comprimento de cada lado da equação e dividi-lo por 2.
 . Para fazer isso, você precisa subtrair o comprimento de cada lado da equação e dividi-lo por 2.
. Para fazer isso, você precisa subtrair o comprimento de cada lado da equação e dividi-lo por 2. , subtraia 16 de cada lado e divida por 2.
, subtraia 16 de cada lado e divida por 2.




4. Anote a resposta final. Não se esqueça de mencionar a unidade das leituras.
 e um comprimento de
e um comprimento de  , torna-se a largura
, torna-se a largura  .
.Método 3 de 4: Usando a diagonal e o comprimento

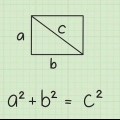
1. Escreva a fórmula da diagonal de um retângulo. A fórmula é  , através do qual
, através do qual  é igual ao comprimento da diagonal,
é igual ao comprimento da diagonal,  igual ao comprimento e
igual ao comprimento e  é igual à largura do retângulo.
é igual à largura do retângulo.
 , através do qual
, através do qual  é igual ao comprimento da diagonal,
é igual ao comprimento da diagonal,  igual ao comprimento e
igual ao comprimento e  é igual à largura do retângulo.
é igual à largura do retângulo. - Este método só funciona para um determinado comprimento da diagonal e o comprimento de um lado do retângulo.
- Esta fórmula também é escrita como
, através do qual
é igual à altura do retângulo e é usado em vez do comprimento. As variáveis
e
consulte as mesmas leituras.

2. Substitua os valores da diagonal e do lado na fórmula. Certifique-se de substituir as variáveis corretas.


3. Quadrado ambos os lados da fórmula. Você precisa fazer isso para se livrar do sinal de radical para que o isolamento da variável largura fique mais fácil.




4. Isolar a variável C  . Você faz isso subtraindo o quadrado do comprimento, de cada lado da equação.
. Você faz isso subtraindo o quadrado do comprimento, de cada lado da equação.
 . Você faz isso subtraindo o quadrado do comprimento, de cada lado da equação.
. Você faz isso subtraindo o quadrado do comprimento, de cada lado da equação. , subtrair 16 de cada lado.
, subtrair 16 de cada lado.


5. Resolva para C  . Você faz isso determinando a raiz quadrada para cada lado da equação.
. Você faz isso determinando a raiz quadrada para cada lado da equação.
 . Você faz isso determinando a raiz quadrada para cada lado da equação.
. Você faz isso determinando a raiz quadrada para cada lado da equação.


6. Anote a resposta final. Não se esqueça de mencionar a unidade das leituras.
 e um lado de
e um lado de  , torna-se a largura
, torna-se a largura  .
.Método 4 de 4: Usando a área ou perímetro e comprimento relativo

1. Escreva a fórmula para a área ou perímetro de um retângulo. Qual fórmula você usa depende dos valores medidos fornecidos. Se a área for dada, use a fórmula da área. Se a circunferência for dada, use a fórmula da circunferência.
- Se a área ou perímetro for desconhecido, ou a relação entre o comprimento e a largura, você não pode usar este método.
- A fórmula da área é
.
- A fórmula da circunferência é
.
- Por exemplo, talvez dado que a área de um retângulo seja 24 cm, então você usa a fórmula para a área de um retângulo.

2. Escreva a expressão que descreve a relação entre o comprimento e a largura. Escreva sua expressão em uma comparação com  .
.
 .
. .
.
3. Substitua a variável eu  na fórmula de área ou perímetro pela expressão para o comprimento. A fórmula agora só ouve a variável
na fórmula de área ou perímetro pela expressão para o comprimento. A fórmula agora só ouve a variável  o que significa que você pode calcular a largura.
o que significa que você pode calcular a largura.
 na fórmula de área ou perímetro pela expressão para o comprimento. A fórmula agora só ouve a variável
na fórmula de área ou perímetro pela expressão para o comprimento. A fórmula agora só ouve a variável  o que significa que você pode calcular a largura.
o que significa que você pode calcular a largura. , então a fórmula fica assim:
, então a fórmula fica assim:


4. Simplifique a equação. A equação simplificada pode assumir diferentes formas, dependendo da relação entre o comprimento e a largura, e dependendo se você está indo para a área ou o perímetro. Tente fazer uma comparação com a qual você  pode resolver o mais facilmente possível.
pode resolver o mais facilmente possível.
 pode resolver o mais facilmente possível.
pode resolver o mais facilmente possível. até
até  .
.
5. Resolva para C  . Novamente, como você
. Novamente, como você  resolve depende da equação simplificada. Use as regras básicas de álgebra e geometria para resolver isso.
resolve depende da equação simplificada. Use as regras básicas de álgebra e geometria para resolver isso.
 . Novamente, como você
. Novamente, como você  resolve depende da equação simplificada. Use as regras básicas de álgebra e geometria para resolver isso.
resolve depende da equação simplificada. Use as regras básicas de álgebra e geometria para resolver isso. pode ser dissolvido da seguinte forma:
pode ser dissolvido da seguinte forma:

Você então tem duas soluções possíveis para
 :
: ou
ou  . Como um retângulo não pode ter largura negativa, você pode excluir -8. Assim é a sua solução
. Como um retângulo não pode ter largura negativa, você pode excluir -8. Assim é a sua solução  .
.Artigos sobre o tópico "Determinando a largura de um retângulo"
Оцените, пожалуйста статью
Similar
Popular