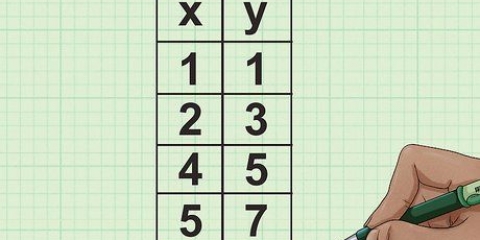
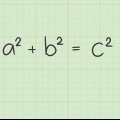Por exemplo: você tem um triângulo com uma base de 15 centímetros e um triângulo correspondente com uma base de 10 cm de comprimento. 
Por exemplo, se você reduzir um triângulo com base 15 cm a um triângulo com base 10 cm, a razão é  .
.
Ao inserir os valores corretos, isso se torna .
. 
Por exemplo: a proporção  pode ser simplificado para
pode ser simplificado para . Assim, o fator de escala de dois triângulos, um com base de 15 cm e outro com base de 10 cm, é
. Assim, o fator de escala de dois triângulos, um com base de 15 cm e outro com base de 10 cm, é  .
. 

Por exemplo, com um fator de escala de 2 você amplia a figura. 
Por exemplo, se a hipotenusa de um triângulo retângulo tiver 5 centímetros de comprimento e o fator de escala for 2, para determinar a hipotenusa do triângulo correspondente, você calcula  . Então o triângulo em escala tem uma hipotenusa de 10 cm.
. Então o triângulo em escala tem uma hipotenusa de 10 cm. 
Por exemplo, se a base de um triângulo retângulo for 3 cm, com um fator de escala de 2, você calcula  para a base do triângulo escalonado. Se a altura de um triângulo retângulo é 4 cm de comprimento, com um fator de escala de 2, então você calcula
para a base do triângulo escalonado. Se a altura de um triângulo retângulo é 4 cm de comprimento, com um fator de escala de 2, então você calcula  para a altura do triângulo escalonado.
para a altura do triângulo escalonado. 

Figuras irregulares podem ser dimensionadas se seus lados forem todos proporcionais. Assim, você pode calcular um fator de escala usando qualquer tamanho fornecido. Como você conhece a largura de qualquer polígono, pode fazer uma equação de razão. Aumentando você usa a proporção  . Se você vai reduzir, você usa a razão
. Se você vai reduzir, você usa a razão  .
. Simplifique a proporção. A proporção  pode ser simplificado para
pode ser simplificado para  . A proporção
. A proporção  pode ser simplificado para
pode ser simplificado para  . Assim, os dois polígonos irregulares têm um fator de escala de
. Assim, os dois polígonos irregulares têm um fator de escala de  ou
ou  .
. 
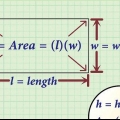
Multiplique a altura do retângulo ABCD pelo fator de escala. Isso lhe dará a altura do retângulo EFGH:  .
. Multiplique a largura do retângulo ABCD pelo fator de escala. Isso lhe dará a largura do retângulo EFGH:  .
. Multiplique a altura e a largura do retângulo EFGH pela área:  . Então, a área do retângulo EFGH é 150 cm2.
. Então, a área do retângulo EFGH é 150 cm2. 

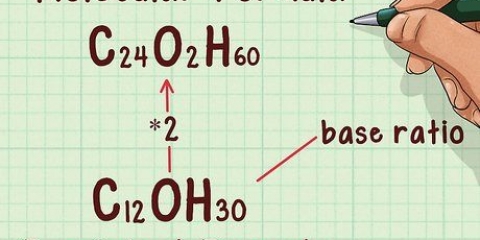
Por exemplo: para determinar a fórmula molecular da substância em questão, multiplique o subscrito de H2O pelo fator de escala 3. H2O * 3 = H6O3 
Por exemplo: o fator de escala para a conexão é 3. A fórmula molecular da substância é H6O3.
Determinando o fator de escala
Contente
O fator de escala (linear) é a razão entre dois lados correspondentes de figuras da mesma forma. Figuras semelhantes têm a mesma forma, mas tamanhos diferentes. O fator de escala é usado para resolver problemas geométricos simples. Você pode usar o fator de escala para determinar os lados desconhecidos de uma figura. Por outro lado, você pode usar o comprimento do lado de dois números semelhantes para calcular o fator de escala. Tais problemas exigem que você multiplique ou simplifique frações.
Degraus
Método 1 de 4: Determinando o fator de escala de uma figura em escala

1. Verifique se as figuras são semelhantes. Figuras da mesma forma têm os mesmos ângulos e os comprimentos dos lados são proporcionais. Figuras semelhantes têm a mesma forma, mas uma figura é maior que a outra.
- A declaração deve indicar que as formas são iguais, ou mostrar que os ângulos são os mesmos, caso contrário, indicar que a razão de comprimento dos lados é proporcional à escala ou que eles correspondem entre si.

2. Encontre um lado correspondente de cada figura. Você pode precisar girar ou virar a figura para que as duas formas se alinhem e você reconheça os lados correspondentes. O comprimento desses dois lados deve ser dado, ou você deve ser capaz de medi-los. Se nenhum comprimento do lado de cada figura for conhecido, você não poderá encontrar o fator de escala.

3. Estabeleça a proporção. Para cada par de figuras correspondentes, há dois fatores de escala: um que você usa quando aumenta uma figura e outro que você usa quando reduz. Se você ampliar para uma versão maior, use a proporção  . Ao redimensionar uma figura, use a proporção
. Ao redimensionar uma figura, use a proporção  .
.
 . Ao redimensionar uma figura, use a proporção
. Ao redimensionar uma figura, use a proporção  .
. .
.Ao inserir os valores corretos, isso se torna
 .
.
4. Simplifique a proporção. A razão simplificada, ou fração, fornece o fator de escala. Se você reduzir o fator de escala será uma fração regular. Se você ampliá-lo se tornar um número inteiro ou uma fração imprópria, que você pode converter em um decimal.
 pode ser simplificado para
pode ser simplificado para . Assim, o fator de escala de dois triângulos, um com base de 15 cm e outro com base de 10 cm, é
. Assim, o fator de escala de dois triângulos, um com base de 15 cm e outro com base de 10 cm, é  .
.Método 2 de 4: Determinando uma figura correspondente usando o fator de escala

1. Determine o comprimento do lado da figura. Você precisa de uma figura cujos lados são dados ou mensuráveis. Se você não puder determinar o comprimento lateral da imagem, não poderá criar uma figura em escala.
- Por exemplo: você tem um triângulo retângulo com lados de 4 cm e 3 cm e uma hipotenusa de 5 cm.

2. Decida se aumentar ou reduzir. Se você aumentar, o número que falta será maior e o fator de escala será um número inteiro, fração imprópria ou decimal. À medida que você encolhe, a figura fica menor e seu fator de escala é provavelmente uma fração regular.

3. Multiplique o comprimento de um lado pelo fator de escala. O fator de escala deve ser dado. Multiplicar o comprimento do lado pelo fator de escala retorna o lado ausente da figura em escala.
 . Então o triângulo em escala tem uma hipotenusa de 10 cm.
. Então o triângulo em escala tem uma hipotenusa de 10 cm.
4. Determine os outros lados da figura. Continue a multiplicar cada lado pelo fator de escala. Isto lhe dará os lados correspondentes da figura que falta.
 para a base do triângulo escalonado. Se a altura de um triângulo retângulo é 4 cm de comprimento, com um fator de escala de 2, então você calcula
para a base do triângulo escalonado. Se a altura de um triângulo retângulo é 4 cm de comprimento, com um fator de escala de 2, então você calcula  para a altura do triângulo escalonado.
para a altura do triângulo escalonado.Método 3 de 4: Alguns exemplos de exercícios

1. Determine o fator de escala dessas figuras correspondentes: um retângulo de 6 cm de altura e um retângulo de 54 cm de altura.
- Compare as duas alturas. Para aumentar, a proporção é
. Para encolher, use a proporção
.
- Simplifique a proporção. A proporção
pode ser simplificado para
. A proporção
pode ser simplificado para
. Portanto, os dois retângulos têm um fator de escala de
ou
.

2. Tente a seguinte tarefa. Um polígono irregular tem 14 cm de comprimento em seu ponto mais largo. Um polígono irregular correspondente tem 8 cm na parte mais larga. Qual é o fator de escala?
 . Se você vai reduzir, você usa a razão
. Se você vai reduzir, você usa a razão  .
. pode ser simplificado para
pode ser simplificado para  . A proporção
. A proporção  pode ser simplificado para
pode ser simplificado para  . Assim, os dois polígonos irregulares têm um fator de escala de
. Assim, os dois polígonos irregulares têm um fator de escala de  ou
ou  .
.
3. Use o fator de escala para responder ao seguinte problema. O retângulo ABCD mede 8 cm x 3 cm. retângulo EFGH é um retângulo maior e correspondente. Dado é um fator de escala de 2,5. Qual é a área do retângulo EFGH?
 .
. .
. . Então, a área do retângulo EFGH é 150 cm2.
. Então, a área do retângulo EFGH é 150 cm2.Método 4 de 4: O fator de escala em química

1. Divida a massa molar de uma substância pela da fórmula empírica. Quando você conhece a fórmula empírica de um composto químico e precisa da fórmula molecular do mesmo produto químico, pode encontrar o fator de escala necessário dividindo a massa molar da substância pela massa molar da fórmula empírica.
- Por exemplo: você quer saber a massa molar de um composto H2O com massa molar de 54,05 g/mol.
- A massa molar de H2O é 18,0152 g/mol.
- Determine o fator de escala dividindo a massa molar do composto pela massa molar da fórmula empírica:
- Fator de escala = 54,05 / 18,0152 = 3

2. Multiplique a fórmula empírica pelo fator de escala. Multiplique o subscrito de cada elemento dentro da fórmula empírica pelo fator de escala que você acabou de calcular. Isso lhe dará a fórmula molecular do composto.

3. Anote a resposta. Com esta resposta você encontrou a resposta correta para a fórmula empírica, bem como a fórmula molecular da ligação química.
Artigos sobre o tópico "Determinando o fator de escala"
Оцените, пожалуйста статью
Similar
Popular