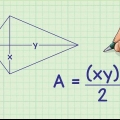
Por exemplo, se você deseja encontrar a área de uma pirâmide hexagonal e sabe que o comprimento de uma borda da base é de 4 cm, você calcula  para encontrar o perímetro da base, porque um hexágono tem seis lados. Então o perímetro da base é 24 cm, então a fórmula para a área ficará assim:
para encontrar o perímetro da base, porque um hexágono tem seis lados. Então o perímetro da base é 24 cm, então a fórmula para a área ficará assim:  .
. 
Suponha que a altura inclinada de uma pirâmide hexagonal seja de 12 cm, então sua fórmula ficará assim:  .
. 
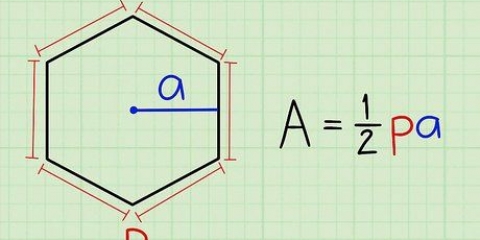
Por exemplo, se você está lidando com uma pirâmide hexagonal, você deve calcule a área do hexágono. A fórmula é  , através do qual
, através do qual  é o comprimento de um lado do hexágono. Como o comprimento de um lado do hexágono é 4 cm, calcule da seguinte forma:
é o comprimento de um lado do hexágono. Como o comprimento de um lado do hexágono é 4 cm, calcule da seguinte forma:




 .
.
Então a área da base é 41,57 centímetros quadrados. 
Suponha que a área da base hexagonal seja 41,57 cm. então sua fórmula para a área ficaria assim:  .
. 
Por exemplo:




Por exemplo:


Portanto, a área total de uma pirâmide hexagonal, com um determinado comprimento de borda de base de 4 cm e uma altura de inclinação de 12 cm, é igual a 185,57 centímetros quadrados. 

Suponha que o comprimento de um lado da base de uma pirâmide quadrada seja 4 cm e a altura da inclinação seja 12 cm, então a fórmula ficaria assim:  .
. 
Por exemplo:



Por exemplo:





Por exemplo:


A área total de uma pirâmide quadrada, com um lado da base de 4 cm e uma altura oblíqua de 12 cm, é, portanto, 112 centímetros quadrados.
Determinando a área de uma pirâmide
Contente
A área de uma pirâmide pode ser encontrada adicionando a área de sua base à área de seus lados. Ao trabalhar com pirâmides regulares, você pode encontrar a área usando uma fórmula, desde que saiba encontrar a área da base da pirâmide. Como a base pode ser um polígono, é útil saber determinar a área de formas como pentágonos e hexágonos. No entanto, ao trabalhar com a pirâmide quadrada regular regular, calcular a área total é fácil, desde que você conheça a altura inclinada da pirâmide e o comprimento da base quadrada.
Degraus
Método 1 de 2: Encontrando a área de uma pirâmide comum

1. Escreva a fórmula para a área de uma pirâmide comum. A fórmula é  , através do qual
, através do qual  é igual a área total da pirâmide,
é igual a área total da pirâmide,  é igual ao perímetro da base,
é igual ao perímetro da base,  é igual à inclinação da pirâmide, e
é igual à inclinação da pirâmide, e  é igual a área da base.
é igual a área da base.
 , através do qual
, através do qual  é igual a área total da pirâmide,
é igual a área total da pirâmide,  é igual ao perímetro da base,
é igual ao perímetro da base,  é igual à inclinação da pirâmide, e
é igual à inclinação da pirâmide, e  é igual a área da base.
é igual a área da base. - A fórmula básica para a área de uma pirâmide, regular ou irregular, é Área Total = Área Base + Área Inclinada.
- Não confunda `altura inclinada` com `altura.A `altura inclinada` é a distância diagonal do topo da pirâmide até a borda da base. A `altura` é a distância perpendicular do topo à base.

2. Calcule o perímetro da base. Se o perímetro não é dado, mas é dado o comprimento de uma aresta da base, você pode calcular o perímetro multiplicando o comprimento de uma aresta pelo número de arestas.
 para encontrar o perímetro da base, porque um hexágono tem seis lados. Então o perímetro da base é 24 cm, então a fórmula para a área ficará assim:
para encontrar o perímetro da base, porque um hexágono tem seis lados. Então o perímetro da base é 24 cm, então a fórmula para a área ficará assim:  .
.
3. Insira o valor da altura da inclinação na fórmula. Certifique-se de usar a altura inclinada, não a altura perpendicular. A altura da inclinação deve ser dada no problema. Se você não souber a altura da inclinação, não poderá usar este método.
 .
.
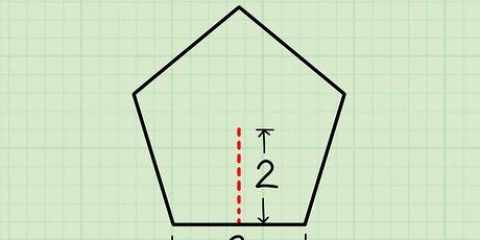
4. Calcule a área da base. Como você faz isso depende da forma da base. Para isso você precisa saber Como determinar as áreas de polígonos.
 , através do qual
, através do qual  é o comprimento de um lado do hexágono. Como o comprimento de um lado do hexágono é 4 cm, calcule da seguinte forma:
é o comprimento de um lado do hexágono. Como o comprimento de um lado do hexágono é 4 cm, calcule da seguinte forma: 



 .
.Então a área da base é 41,57 centímetros quadrados.

5. Aplique a área da base na fórmula. Certifique-se de ter a variável  substitui.
substitui.
 substitui.
substitui. .
.
6. Multiplique o perímetro da base pela altura inclinada da pirâmide. Divida o produto por dois. Isso lhe dá a área inclinada das faces da pirâmide.




7. Some os dois valores. A soma é a área inclinada mais a área da base, então você obtém a área total da pirâmide em unidades quadradas.


Portanto, a área total de uma pirâmide hexagonal, com um determinado comprimento de borda de base de 4 cm e uma altura de inclinação de 12 cm, é igual a 185,57 centímetros quadrados.
Método 2 de 2: Encontrando a área de uma pirâmide quadrada

1. Escreva a fórmula da área de uma pirâmide quadrada. A fórmula é  , através do qual
, através do qual  é igual ao comprimento de um lado da base, e
é igual ao comprimento de um lado da base, e  é igual à inclinação da pirâmide.
é igual à inclinação da pirâmide.
 , através do qual
, através do qual  é igual ao comprimento de um lado da base, e
é igual ao comprimento de um lado da base, e  é igual à inclinação da pirâmide.
é igual à inclinação da pirâmide. - Não confunda `altura inclinada` com `altura.A `altura inclinada` é a distância diagonal do topo da pirâmide até a borda da base. A `altura` é a distância perpendicular do topo à base.
- Observe que esta fórmula é apenas outra maneira de calcular Área Total = Área Base (
) + Superfície inclinada (
) escrever. Esta fórmula só funciona para pirâmides quadradas regulares.

2. Insira os valores do comprimento dos lados e da altura da inclinação na fórmula. Certifique-se de substituir o comprimento do lado da base com  e a altura inclinada por
e a altura inclinada por  .
.
 e a altura inclinada por
e a altura inclinada por  .
. .
.
3. Esquadre o comprimento de um lado da base. Isso lhe dará a área da base.



4. Multiplique o comprimento de um lado da base pela altura da inclinação e divida por dois. Então multiplique por quatro. Isso lhe dará a superfície angular da pirâmide.





5. Adicione a área da base a essa área inclinada. Isso lhe dará a área total da pirâmide, em unidades quadradas.


A área total de uma pirâmide quadrada, com um lado da base de 4 cm e uma altura oblíqua de 12 cm, é, portanto, 112 centímetros quadrados.
Necessidades
- Lápis
- Papel
- Calculadora (opcional)
- Régua (opcional)
Artigos sobre o tópico "Determinando a área de uma pirâmide"
Оцените, пожалуйста статью
Popular