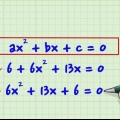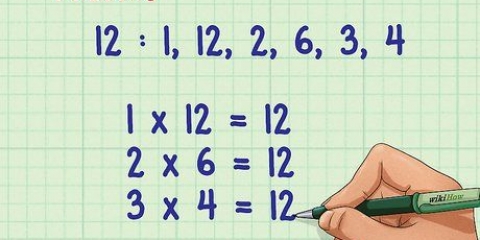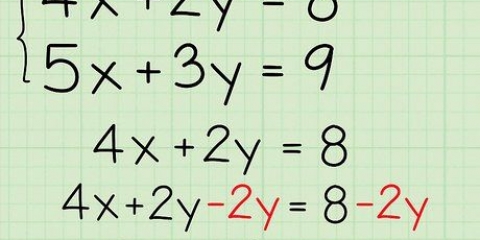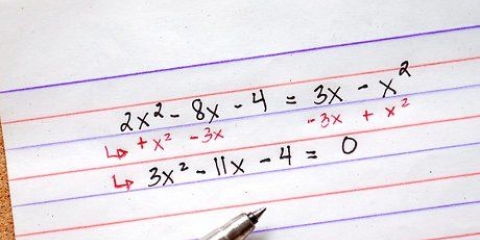Por exemplo: se você quiser dividir 20 em fatores, você pode escrever isso como 4×5. Observe que os termos variáveis também podem ser escritos como fatores. - Por exemplo, 20x pode ser escrito como 4(5x). Os números primos não podem ser escritos como fatores porque são divisíveis apenas por eles mesmos e 1. 
Hãmorcegos mlevantar oito Ccontração muscular Vmultiplicar delen Ocontar umasubtrair 

Por exemplo, vamos encontrar os termos semelhantes em nossa equação 1 + 2x - 3 + 4x. 2x e 4x ambos têm a mesma variável elevada à mesma potência (neste caso, as variáveis x não têm nenhum expoente). Além disso, 1 e -3 são termos iguais, porque nenhum deles tem uma variável. Então nesta equação estão 2x e 4x e 1 e-3 termos iguais. 
Somamos os termos semelhantes em nosso exemplo. 2x + 4x = 6x 1 + -3 = -2 
Em nosso exemplo, os termos simplificados eram 6x e -2, então a nova expressão se torna 6x - 2. Esta expressão simplificada é equivalente à original (1 + 2x - 3 + 4x), mas é mais curta e mais fácil de calcular com. É mais fácil fatorar, o que, como veremos a seguir, é uma habilidade importante para poder simplificar. 
Por exemplo, suponha que temos a equação 5(3x-1) + x((2x)/(2)) + 8 - 3x. Então seria incorreto considerar imediatamente 3x e 2x como termos iguais e combiná-los, porque os parênteses na expressão ditam que temos que fazer outras operações primeiro. Primeiro, vamos realizar as operações aritméticas na expressão de acordo com a ordem das operações, para obter os termos que temos Nós vamos pode usar. Ver abaixo: 5(3x-1) + x((2x)/(2)) + 8 - 3x 15x - 5 + x(x) + 8 - 3x 15x - 5 + x + 8 - 3x. passar agora como as únicas operações restantes são adição e subtração, podemos combinar os termos semelhantes. x + (15x - 3x) + (8 - 5) x + 12 x + 3 

Vamos fatorar nossa equação usando o máximo divisor comum, 3. Fazemos isso dividindo cada termo por 3. 9x/3 = 3x 27x/3 = 9x -3/3 = -1 Então a nova expressão é 3x + 9x - 1. 
Para nossa expressão de exemplo, 3x + 9x - 1, colocamos a expressão entre parênteses e multiplicamos esse termo pelo máximo divisor comum da equação original para converter 3(3x + 9x - 1) para obter. Esta equação é equivalente ao original, 9x + 27x - 3. 
Suponha que nossa expressão de exemplo original, 9x + 27x - 3, seja igual ao numerador de uma fração maior com 3 como denominador. Esta fração fica assim: (9x + 27x - 3)/3. Podemos usar a fatoração para simplificar essa fração. Adicione a forma fatorada da nossa expressão original ao numerador: (3(3x + 9x - 1))/3 Observe que tanto o numerador quanto o denominador têm 3 como coeficiente. Se você dividir o numerador e o denominador por 3, obtém: (3x + 9x - 1)/1. Porque uma fração com "1" no denominador é igual aos termos no numerador, podemos dizer que nossa fração original pode ser simplificada para 3x + 9x - 1. 

Vamos dar um exemplo simples - √(90). Se tomarmos o número 90 como um produto dos dois fatores, 9 e 10, podemos calcular a raiz quadrada de 9 para obter 3 e colocá-lo na frente do radical. Em outras palavras: (90) √(9×10) (√(9) × √(10)) 3 × √(10) 3√(10) 
Por exemplo, suponha que temos a expressão 6x × 8x + (x/x). Em qualquer caso em que seja necessário multiplicar ou dividir expoentes, subtraímos ou somamos os expoentes respectivamente, para resolver rapidamente um termo simplificado. Ver abaixo: 6x × 8x + (x/x) (6×8)x + (x) 48x+x Para uma explicação, veja abaixo: Multiplicar termos exponenciais é essencialmente o mesmo que multiplicar longas séries de termos sem expoentes. Por exemplo, porque x = x × x × x e x= x × x × x × x × x, x × x = (x × x × x) × (x × x × x × x × x), ou x. Da mesma forma, dividir termos exponenciais é o mesmo que dividir longas sequências de termos sem expoentes. x/x = (x × x × x × x × x)/(x × x × x). Como qualquer termo no numerador pode ser cancelado contra o mesmo termo no denominador, ficamos com duas vezes um x no numerador e nenhum no denominador, deixando-nos com x como resposta.
Simplificando equações matemáticas
Contente
Ser capaz de simplificar equações algébricas é uma parte essencial do domínio do básico da álgebra e uma ferramenta extremamente valiosa para todos os matemáticos. A simplificação permite que um matemático mude uma expressão complexa, longa e/ou desajeitada para uma forma mais simples ou mais conveniente, mas equivalente. O básico da simplificação é muito fácil de aprender - mesmo para alguém que odeia matemática. Seguindo alguns passos simples, é possível simplificar muitas das expressões algébricas mais comuns sem nenhum conhecimento matemático especial.
Degraus
Método 1 de 4: Entendendo os principais conceitos

1. Determinar "termos iguais" de acordo com suas variáveis e poderes. Possuir em álgebra "termos iguais" sobre as mesmas variáveis, elevado à mesma potência. Em outras palavras, dois termos são "semelhante", quando eles têm a(s) mesma(s) variável(eis), ou nenhuma(s), e quando cada variável tem o mesmo poder, ou nenhum. A ordem das variáveis dentro de um termo não importa.
- Por exemplo, 3x e 4x são termos iguais porque cada termo tem uma variável x elevada à segunda potência. As variáveis x e x não são termos iguais, porque x tem uma potência diferente em cada termo. Da mesma forma, -3yx e 5xz não são termos iguais, porque cada termo é composto de diferentes variáveis.

2. Fatorar escrevendo os números como o produto de dois fatores. A fatoração é uma maneira de escrever um determinado número como o produto de dois fatores. Os números podem consistir em vários fatores – por exemplo, o número 12, que pode ser formado por 1 × 12, 2 × 6 e 3 × 4, de modo que podemos dizer que 1, 2, 3, 4, 6 e 12 são todos fatores de 12. Outra maneira de ver isso é que os fatores de um número são os números pelos quais ele é divisível.

3. Use o mnemônico `Como devemos nos livrar das inadequações` (ou como acrônimo HMWVDOA) para lembrar a ordem das operações. Às vezes, simplificar uma expressão é apenas realizar as operações na expressão até que nada mais possa ser feito. Nesse caso é importante saber a ordem das operações, para evitar erros de cálculo. Este mnemônico pode ajudá-lo a lembrar a ordem das edições - as letras correspondem ao tipo de edições que você precisa realizar e em que ordem. Se houver multiplicações e divisões no mesmo problema, você terá que realizar essas operações da esquerda para a direita quando chegar a esse ponto. O mesmo vale para adição e subtração. A imagem acima dá uma resposta que não está correta. O último passo não funcionou adição e subtração da esquerda para a direita. Primeiro foi adicionado. Deve haver 25 - 20 = 5 e depois 5 + 6 = 11.
Método 2 de 4: Combinando termos semelhantes

1. Anote suas equações. As equações matemáticas mais simples (aquelas com apenas algumas variáveis e coeficientes como números inteiros, sem frações, raízes quadradas, etc.).) muitas vezes pode ser resolvido em poucos passos. Tal como acontece com a maioria dos problemas de matemática, o primeiro passo para simplificar uma equação é escrever a equação!
- Para os próximos passos tomamos a expressão 1 + 2x - 3 + 4x como um exemplo.

2. Determine quais são os termos semelhantes. Agora procure os termos semelhantes em sua equação. Lembre-se de que termos semelhantes têm a(s) mesma(s) variável(is) e expoente(s).

3. Combinar termos semelhantes. Agora que você determinou os termos semelhantes, você pode começar a combiná-los para simplificar sua equação. Some os termos (ou subtraia-os no caso de termos negativos) para simplificar cada conjunto de termos (com as mesmas variáveis e expoentes) em um termo.

4. Faça uma expressão simplificada de seus termos simplificados. Depois de combinar seus termos semelhantes, construa uma expressão a partir de seu novo e menor conjunto de termos. Agora você deve ter uma expressão mais simples com um termo para cada conjunto de variáveis e expoentes na expressão original. Esta nova expressão é equivalente à primeira.

5. Aderir à ordem das operações ao combinar termos semelhantes. Em expressões muito simples como as que tratamos nos exercícios acima, reconhecer os termos semelhantes é fácil. Nas expressões mais complexas, como aquelas com termos entre parênteses, frações e raízes, a combinação de termos semelhantes não será imediatamente óbvia. Nesses casos, siga a sequência de operações e execute as operações nos termos da sua expressão até ficar apenas com adição e subtração.
Método 3 de 4: fatoração

1. Encontre o máximo divisor comum na expressão. A fatoração é uma maneira de simplificar expressões removendo fatores que aparecem em todos os termos da expressão. Para começar, encontre o máximo divisor comum de todos os termos da expressão — em outras palavras, o maior número pelo qual todos os termos da expressão são divisíveis por.
- Suponha que tomemos a equação 9x + 27x - 3. Note que todo termo nesta equação é divisível por 3. Porque não dos termos é totalmente divisível por outro número maior, podemos dizer que 3 é o maior denominador comum da nossa expressão.

2. Divida os termos na expressão pelo máximo divisor comum. Em seguida, divida cada termo em sua equação pelo máximo divisor comum que você acabou de encontrar. Todos os termos resultantes terão coeficientes menores do que os da expressão original.

3. Escreva sua expressão como o produto do máximo divisor comum e os termos restantes. Sua nova expressão não é a mesma que a antiga, então não é correto dizer que é a versão simplificada. Para tornar a nova expressão igual à antiga, teremos que levar em conta que ela é dividida pelo máximo divisor comum. Coloque sua nova expressão entre parênteses e escreva o máximo divisor comum da equação original como o coeficiente da expressão também entre parênteses.

4. Fator para simplificar frações. Agora você pode estar se perguntando por que a fatoração é útil se a nova expressão tiver que ser multiplicada novamente após a remoção do máximo divisor comum. A fatoração permite que um matemático use vários truques para simplificar uma expressão. Um dos truques mais fáceis usa o fato de que multiplicar o numerador e o denominador de uma fração pelo mesmo número produz uma fração nas mesmas proporções. Ver abaixo:
Método 4 de 4: Aplicar simplificar

1. Simplifique frações dividindo por fatores iguais. Como mencionado acima, se o numerador e o denominador de uma expressão tiverem os mesmos fatores, esses fatores podem ser removidos da fração. Às vezes, isso requer que o numerador, o denominador ou ambos sejam fatorados (como foi o caso no exemplo acima), enquanto em outros casos os fatores compartilhados são imediatamente aparentes. Observe que também é possível dividir os termos individuais no numerador pela expressão no denominador, para obter uma expressão simplificada.
- Vamos abordar um exemplo que não exige necessariamente que você os escreva para simplificar. Suponha que você tenha a fração (5x + 10x + 20)/10, você pode dividir cada termo no numerador pelo 10 no denominador, para simplificar o todo, mesmo que o "5" em 5x não maior que 10 e não é possível escolher 10 como fator.
- Fazendo isso, obtemos ((5x)/10) + x + 2. Se quisermos, podemos reescrever o primeiro termo como (1/2)x para obter (1/2)x + x + 2.

2. Use raízes quadradas para simplificar raízes. Expressões sob o sinal de uma raiz quadrada são chamadas de equações de raiz quadrada. Você pode simplificar isso determinando as raízes quadradas (fatores que formam uma segunda potência de um inteiro), após o que você subtrai a raiz quadrada desses fatores para removê-los do sinal de radical.

3. Some os expoentes ao multiplicar dois termos exponenciais e subtraia-os ao dividir. Algumas equações algébricas requerem multiplicar ou dividir termos exponenciais. Você não calcula cada termo exponencial e não multiplica ou divide manualmente, mas contar você soma os expoentes de cada termo quando os multiplica e você os puxa quando você os compartilha, economizando muito tempo. Você também pode aplicar este conceito para simplificar equações com múltiplas variáveis.
Pontas
- Lembre-se que você deve considerar esses números como positivos ou negativos. Muitas pessoas ficam presas com isso e pensam, "Que sinal devo colocar aqui?"
- Peça ajuda se precisar!
- Simplificar equações matemáticas não é fácil, mas depois que você pegar o jeito, poderá usá-lo pelo resto da vida.
Avisos
- Tenha cuidado para não adicionar acidentalmente alguns números extras, expoentes ou operações que não pertencem a eles.
- Sempre preste atenção aos termos iguais e não deixe os expoentes te enganarem.
Artigos sobre o tópico "Simplificando equações matemáticas"
Оцените, пожалуйста статью
Popular