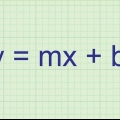Determinando o Coeficiente de Correlação

Contente

Degraus
Pontas
Avisos

O coeficiente de correlação, denotado como r ou ρ, é a medida da correlação linear (a relação, tanto em força quanto em direção) entre duas variáveis. Varia de -1 a +1, usando sinais de mais e menos para representar a correlação positiva e negativa. Se o coeficiente de correlação for exatamente -1, então a relação entre as duas variáveis é completamente negativa; se o coeficiente de correlação for exatamente +1, então a relação é completamente positiva. Duas variáveis podem ter uma correlação positiva, uma correlação negativa ou nenhuma correlação. Você pode calcular a correlação manualmente, usando algumas calculadoras de correlação gratuitas disponíveis online ou usando as funções estatísticas de uma boa calculadora gráfica.

Degraus

Método 1 de 4: Calculando o coeficiente de correlação manualmente

Imagem intitulada Encontre o coeficiente de correlação Passo 1

1. Colete seus dados primeiro. Para começar a calcular uma correlação eficiente, primeiro examine os pares de dados. É útil colocá-los em uma tabela, tanto na vertical quanto na horizontal. Rotule cada linha ou coluna x e y.

Por exemplo: suponha que você tenha quatro pares de dados para X e y. A tabela poderia então ficar assim:

x || y
1 || 1
2 || 3
4 || 5
5 || 7

Imagem intitulada Encontre o coeficiente de correlação Etapa 2

2. Calcule a média de X. Para calcular a média, você precisa somar todos os valores de X somar e depois dividir pelo número de valores.

Partindo do exemplo acima, observe que você tem quatro valores para X. Para calcular a média, conte todos os valores para X e divida por 4. O cálculo então fica assim:

μ X = (1 + 2 + 4 + 5) / 4

${estilo de exibição mu _{x}=(1+2+4+5)/4}$

μ X = 12 / 4

${estilo de exibição mu _{x}=12/4}$

μ X = 3

${estilo de exibição mu _{x}=3}$

Imagem intitulada Encontre o coeficiente de correlação Etapa 3

3. Encontre a média de y. Para obter a média de y Para encontrá-lo, siga os mesmos passos, somando todos os valores de y e depois dividindo pelo número de valores.

No exemplo acima, você também tem quatro valores para y. Some todos esses valores e depois divida por 4. Os cálculos ficarão assim:

μ y = (1 + 3 + 5 + 7) / 4

${estilo de exibição mu _{y}=(1+3+5+7)/4}$

μ y = 16 / 4

${displaystyle mu _{y}=16/4}$

μ y = 4

${displaystyle mu _{y}=4}$

Imagem intitulada Encontre o coeficiente de correlação Etapa 4

4. Determine o desvio padrão de X. Depois de ter seus meios, você pode calcular o desvio padrão. Use a fórmula para isso:

Σ X = \sqrt{} 1 n - 1 Σ (X - μ_{X})^{2}

${displaystyle sigma _{x}={sqrt {{frac {1}{n-1}}Sigma (x-mu _{x})^{2}}}}$

Com os dados de amostra, seus cálculos ficarão assim:

Σ X = \sqrt{} 1 4 - 1 * ((1 - 3)^{2} + (2 - 3)^{2} + (4 - 3)^{2} + (5 - 3)^{2})

${displaystyle sigma _{x}={sqrt {{frac {1}{4-1}}*((1-3)^{2}+(2-3)^{2}+(4 -3)^{2}+(5-3)^{2})}}}$

Σ X = \sqrt{} \frac{1}{3} * (4 + 1 + 1 + 4)

${displaystyle sigma _{x}={sqrt {{frac {1}{3}}*(4+1+1+4)}}}$

Σ X = \sqrt{} \frac{1}{3} * (10)

${displaystyle sigma _{x}={sqrt {{frac {1}{3}}*(10)}}}$

Σ X = \sqrt{\frac{10}{3}}

${displaystyle sigma _{x}={sqrt {frac {10}{3}}}}$

Σ X = 1, 83

${displaystyle sigma _{x}=1,83}$

Imagem intitulada Encontre o coeficiente de correlação Etapa 5

5. Calcule o desvio padrão de y. Usando os mesmos passos básicos, encontre o desvio padrão de y. Você vai usar a mesma fórmula, usando os pontos de dados para y.

Com os dados de amostra, seus cálculos ficarão assim:

Σ y = \sqrt{} 1 4 - 1 * ((1 - 4)^{2} + (3 - 4)^{2} + (5 - 4)^{2} + (7 - 4)^{2})

${displaystyle sigma _{y}={sqrt {{frac {1}{4-1}}*((1-4)^{2}+(3-4)^{2}+(5 -4)^{2}+(7-4)^{2})}}}$

Σ y = \sqrt{} \frac{1}{3} * (9 + 1 + 1 + 9)

${displaystyle sigma _{y}={sqrt {{frac {1}{3}}*(9+1+1+9)}}}$

Σ y = \sqrt{} \frac{1}{3} * (20)

${displaystyle sigma _{y}={sqrt {{frac {1}{3}}*(20)}}}$

Σ y = \sqrt{\frac{20}{3}}

${displaystyle sigma _{y}={sqrt {frac {20}{3}}}}$

Σ y = 2, 58

${displaystyle sigma _{y}=2,58}$

Imagem intitulada Encontre o Coeficiente de Correlação Passo 6

6. Veja a fórmula básica para determinar um coeficiente de correlação. A fórmula para calcular um coeficiente de correlação usa médias, desvios padrão e o número de pares em um conjunto de dados (representado por n). O próprio coeficiente de correlação é representado pela letra minúscula r ou pela letra grega ρ (rho). Para este artigo, usaremos a fórmula conhecida como coeficiente de correlação de Pearson, conforme mostrado abaixo:

ρ = (1 n - 1) Σ (X - μ X Σ_{X}) * (y - μ y Σ_{y})

${displaystyle rho =left({frac {1}{n-1}}right)Sigma left({frac {x-mu _{x}}{sigma _{x}} }right)*left({frac {y-mu _{y}}{sigma _{y}}}right)}$

Você pode notar pequenas variações na fórmula, aqui ou em outras explicações. Por exemplo, alguns usarão a notação grega com rho e sigma, enquanto outros usarão r e s. Algumas explicações podem usar fórmulas ligeiramente diferentes, mas serão matematicamente equivalentes a esta.

Imagem intitulada Encontre o Coeficiente de Correlação Passo 7

7. Determine o coeficiente de correlação. Agora você tem as médias e os desvios padrão para suas variáveis, então você pode passar para a fórmula do coeficiente de correlação. Lembre-se disso n representa o número de valores que você tem. Você já elaborou as outras informações relevantes nas etapas acima.

Usando os dados de amostra, você pode inserir os dados na fórmula do coeficiente de correlação e calculá-los assim:

ρ = (1 n - 1) Σ (X - μ X Σ_{X}) * (y - μ y Σ_{y})

${displaystyle rho =left({frac {1}{n-1}}right)Sigma left({frac {x-mu _{x}}{sigma _{x}} }right)*left({frac {y-mu _{y}}{sigma _{y}}}right)}$

ρ = (\frac{1}{3}) *

${displaystyle rho =left({frac {1}{3}}right)*}$ [

(1 - 3 1, 83) * (1 - 4 2, 58) + (2 - 3 1, 83) * (3 - 4 2, 58)

${displaystyle left({frac {1-3}{1.83}}right)*left({frac {1-4}{2.58}}right)+left({ frac {2- 3}{1.83}}right)*left({frac {3-4}{2.58}}right)}$

+ (4 - 3 1, 83) * (5 - 4 2, 58) + (5 - 3 1, 83) * (7 - 4 2, 58)

${displaystyle +left({frac {4-3}{1.83}}right)*left({frac {5-4}{2.58}}right)+left({ frac {5 -3}{1.83}}right)*left({frac {7-4}{2.58}}right)}$ ]

ρ = (\frac{1}{3}) * (6 + 1 + 1 + 6 4, 721)

${displaystyle rho =left({frac {1}{3}}right)*left({frac {6+1+1+6}{4.721}}right)}$

ρ = (\frac{1}{3}) * 2, 965

${displaystyle rho =left({frac {1}{3}}right)*2.965}$

ρ = (2, 965 3)

${displaystyle rho =left({frac {2.965}{3}}right)}$

ρ = 0, 988

${displaystyle rho =0,988}$

Imagem intitulada Encontre o Coeficiente de Correlação Passo 8

8. Interprete o resultado. Para este conjunto de dados, o coeficiente de correlação é de 0,988. Este número diz duas coisas sobre os dados. Olhe para o sinal do número e o tamanho do número.

Como o coeficiente de correlação é positivo, pode-se dizer que existe uma correlação positiva entre os dados x e os dados y. Isso significa que, à medida que os valores de x aumentam, você espera que os valores de y também aumentem.

Como o coeficiente de correlação é muito próximo de +1, os dados x e y estão intimamente relacionados. Se você fizesse um gráfico desses pontos, veria que eles são uma boa aproximação de uma linha reta.

Método 2 de 4: Usando calculadoras de correlação online

Imagem intitulada Encontre o Coeficiente de Correlação Passo 9

1. Pesquise online por calculadoras de correlação. Medir a correlação é um cálculo bastante padrão para estatísticos. O cálculo pode ser muito tedioso para grandes conjuntos de dados se feito à mão. Portanto, muitas fontes disponibilizaram cálculos de correlação comuns online. Use qualquer mecanismo de pesquisa e digite o termo de pesquisa `calculadora de correlação`.

Imagem intitulada Encontre o Coeficiente de Correlação Passo 10

2. Para os dados em. Por favor, leia atentamente as instruções no site para que você possa inserir os dados corretamente. É importante que os pares de dados sejam mantidos em ordem ou você obterá um resultado de correlação incorreto. Sites diferentes usam formatação diferente para inserir dados.

Por exemplo: no site http://ncalculators.com/statistics/correlation-coeficiente-calculator.htm encontre uma caixa horizontal para inserir valores x e uma segunda caixa horizontal para inserir valores y. Você insere os termos separados apenas por vírgulas. Portanto, o conjunto de dados x calculado anteriormente neste artigo deve ser inserido como 1,2,4,5. O conjunto de dados y é inserido como 1,3,5,7.

Em outro site, http://www.álcool.com/calculators/statistics/coeficiente de correlação/, você pode inserir dados horizontalmente e verticalmente, desde que mantenha os pontos de dados em ordem.

Imagem intitulada Encontre o Coeficiente de Correlação Passo 11

3. Calcule os resultados. Esses sites de cálculo são populares porque, em geral, depois de inserir os dados, tudo o que você precisa fazer é clicar no botão `Calcular` - o resultado aparecerá automaticamente.

Método 3 de 4: Usando uma calculadora gráfica

Imagem intitulada Encontre o Coeficiente de Correlação Passo 12

1. Insira seus dados. Em sua calculadora gráfica, ative a função de estatísticas e selecione o comando `Editar`.

Cada calculadora tem comandos de tecla ligeiramente diferentes. Este artigo fornece instruções específicas para a Texas Instruments TI-86.
Entre na função Stat pressionando [2nd]-Stat (acima da tecla `+`) e depois F2-Edit.

Imagem intitulada Encontre o Coeficiente de Correlação Passo 13

2. Limpar todos os dados salvos antigos. A maioria das calculadoras manterá os dados estatísticos até que sejam apagados. Para garantir que você não confunda dados antigos com dados novos, você deve primeiro limpar todas as informações armazenadas anteriormente.

Use as teclas de seta para mover o cursor para destacar a categoria `xStat`. Em seguida, pressione `Limpar` e `Enter. Isso deve limpar todos os valores na coluna xStat.

Use as teclas de seta para destacar a categoria `yStat`. Pressione `Clear` e `Enter` para limpar os dados dessa coluna também.

Imagem intitulada Encontre o Coeficiente de Correlação Passo 14

3. Insira seus valores de dados. Use as teclas de seta para mover o cursor para o primeiro espaço abaixo do título xStat. Digite seu primeiro valor de dados e pressione Enter. Você deve ver o espaço na parte inferior da tela `xStat(1)=__` onde seu valor preenche o espaço vazio. Quando você pressionar Enter, os dados preencherão a tabela, o cursor se moverá para a próxima linha e a linha na parte inferior da tela agora deve ler `xStat(2)=__`.

Continue inserindo todos os valores x.

Depois de inserir os valores x, use as teclas de seta para mover para a coluna yStat e insira os valores y.

Quando todos os dados tiverem sido inseridos, pressione Exit para limpar a tela e sair do menu Stat.

Imagem intitulada Encontre o Coeficiente de Correlação Passo 15

4. Calcular as estatísticas de regressão linear. O coeficiente de correlação é uma medida de quão bem os dados se aproximam de uma linha reta. Uma calculadora gráfica com funções estatísticas pode calcular muito rapidamente a linha de melhor ajuste e o coeficiente de correlação.

Entre na função Stat e pressione o botão Calc. Na TI-86 é [2nd][Stat][F1].

Escolha os cálculos de regressão linear. Na TI-86, é [F3], rotulado "LinR.` A tela gráfica mostrará então a linha `LinR _` com um cursor piscando.

Agora você precisa inserir os nomes das duas variáveis que deseja calcular. Estes são xStat e yStat.

Na TI-86, selecione a lista de nomes (`Names`) pressionando [2nd][List][F3].

A linha inferior da tela agora deve mostrar as variáveis disponíveis. Escolha [xStat] (provavelmente é o botão F1 ou F2), digite uma vírgula e depois [yStat].

Pressione Enter para calcular os dados

Imagem intitulada Encontre o Coeficiente de Correlação Passo 16

5. Interprete os resultados. Ao pressionar Enter, a calculadora calculará imediatamente as seguintes informações para os dados inseridos:

y = uma + b X

${estilo de exibição y=a+bx}$ : Esta é a fórmula geral para uma linha reta. No entanto, em vez do conhecido `y=mx+b`, isso é apresentado na ordem inversa.

uma =

${ estilo de exibição a=}$ . Este é o valor da intersecção com o eixo y da linha que melhor se ajusta.

b =

${estilo de exibição b=}$ . Esta é a inclinação da linha que melhor se ajusta.

correto =

${displaystyle {text{corr}}=}$ . Este é o coeficiente de correlação.

n =

${estilo de exibição n=}$ . Este é o número de pares de dados usados no cálculo.

Método 4 de 4: Repetindo o Básico

Imagem intitulada Encontre a Etapa do Coeficiente de Correlação 17

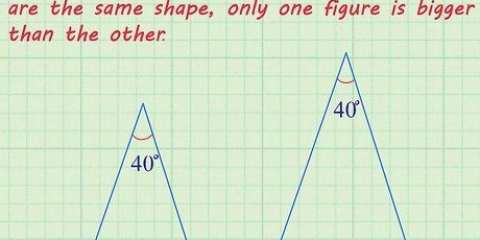
1. Entenda o conceito de correlação. Correlação refere-se à relação estatística entre duas quantidades. O coeficiente de correlação é um único número que você pode calcular para dois conjuntos de pontos de dados. O número é sempre algo entre -1 e +1 e indica o quão próximo os dois conjuntos de dados estão conectados.

Por exemplo, se você medisse a altura e a idade de crianças até cerca de 12 anos de idade, esperaria encontrar uma forte correlação positiva. À medida que as crianças crescem, elas tendem a ficar mais altas.
Um exemplo de correlação negativa é comparar o tempo que alguém passa praticando golfe e a pontuação de golfe dessa pessoa. Conforme a prática progride, a pontuação deve cair.
Em última análise, você esperaria pouca correlação, positiva ou negativa, entre o tamanho do sapato de uma pessoa, por exemplo, e suas notas nos exames.

Imagem intitulada Encontre a Etapa do Coeficiente de Correlação 18

2. Calcule a média. A média aritmética, ou "média", de um conjunto de dados é calculada somando todos os valores dos dados e depois dividindo pelo número de valores no conjunto. Quando você deseja determinar o coeficiente de correlação para seus dados, você precisa calcular a média de cada conjunto de dados.

A média de uma variável é indicada pela variável com uma linha horizontal acima dela. Isso é muitas vezes referido como `x-bar` ou `y-bar` para os conjuntos de dados de x e y. Alternativamente, a média pode ser denotada pela letra grega minúscula μ (mu). Por exemplo, para representar a média dos pontos de dados de x, você pode usar μ_X ou μ(x).

Por exemplo, se você tiver um conjunto de x (1,2,5,6,9,10), a média desses dados seria calculada da seguinte forma:

μ X = (1 + 2 + 5 + 6 + 9 + 10) / 6

${estilo de exibição mu _{x}=(1+2+5+6+9+10)/6}$

μ X = 33 / 6

${estilo de exibição mu _{x}=33/6}$

μ X = 5, 5

${estilo de exibição mu _{x}=5,5}$

Imagem intitulada Encontre a Etapa do Coeficiente de Correlação 19

3. Saiba a importância do desvio padrão. Na estatística, o desvio padrão mede a variação, mostrando a dispersão dos números em relação à média. Um grupo de números com um baixo desvio padrão são bastante próximos uns dos outros. Um grupo de números com alto desvio padrão é mais disperso.

Como símbolo, o desvio padrão é expresso com a letra minúscula s ou a letra grega σ (sigma). Assim, o desvio padrão dos dados x é escrito como s_X ou_X.

Imagem intitulada Encontre o Coeficiente de Correlação Passo 20

4. Reconhecer a notação de somatória. O operador de soma é um dos operadores mais comuns em matemática, representando uma soma de valores. É representado pela letra maiúscula grega, sigma ou ∑.

Por exemplo, se você tiver um conjunto de pontos de dados x (1,2,5,6,9,10), então ∑x significa:

1+2+5+6+9+10 = 33

Pontas

O coeficiente de correlação às vezes é chamado de coeficiente de correlação do momento do produto de Pearson, em homenagem a Karl Pearson, seu desenvolvedor.
Em geral, um coeficiente de correlação maior que 0,8 (positivo ou negativo) representa uma correlação forte; um coeficiente de correlação inferior a 0,5 (novamente positivo ou negativo) representa um coeficiente de correlação fraco.

Avisos

A correlação mostra que dois conjuntos de dados estão de alguma forma conectados. No entanto, tenha cuidado para não interpretar isso como uma relação causal. Por exemplo, se você comparar o tamanho dos sapatos das pessoas e sua altura, provavelmente encontrará uma forte correlação positiva. Pessoas maiores geralmente têm pés maiores. No entanto, isso não significa que ficar alto fará seus pés crescerem, ou que pés grandes o deixarão alto. Eles simplesmente acontecem juntos.