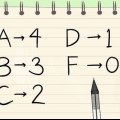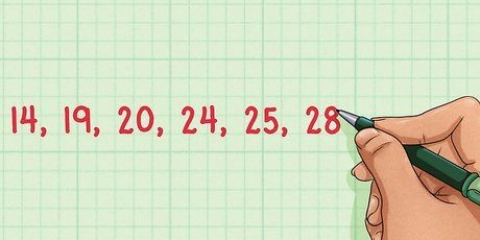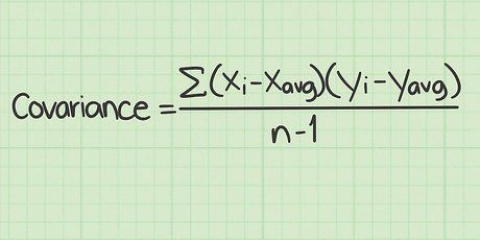Como Calcular o Coeficiente de Correlação de Rank de Spearman

Contente

Degraus
Pontas
Avisos

Com o coeficiente de correlação de postos de Spearman você pode ver se duas variáveis estão relacionadas por uma função monotônica (d.C.z. que se um número aumenta, o outro número também aumenta ou vice-versa). Para calcular o coeficiente de correlação de posto de Spearman, você deve ordenar e comparar os conjuntos de dados para encontrar Σd e, em seguida, inserir esse valor na versão padrão ou simplificada da fórmula do coeficiente de correlação de posto de Spearman. Você também pode calcular esse coeficiente com fórmulas do Excel ou comandos R.

Degraus

Método 1 de 3: manualmente

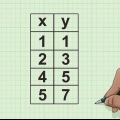
1. Desenhe sua tabela de dados. Organiza as informações necessárias para calcular o coeficiente de correlação de classificação de Spearman. Você precisa:

6 colunas de títulos, como mostrado acima.
Quantas linhas você tiver pares de dados.

2. Preencha as duas primeiras colunas com seus pares de dados.

3. Organize os pontos de dados da primeira coluna na terceira coluna, de 1 a n (o número total de pontos de dados que você tem). Dê a posição 1 do número mais baixo, a posição 2 do próximo número e assim por diante.

4. Faça o mesmo com a quarta coluna como no passo 3, mas agora organize a segunda coluna.

Se você tiver dois (ou mais) pontos de dados com o mesmo valor em uma coluna, tire a média das posições que esses pontos de dados normalmente teriam e dê aos pontos de dados essa média como sua nova posição.
No exemplo à direita existem dois cincos que normalmente estariam na posição 2 e 3. São duas as mesmas músicas, então tire a média de suas posições. A média de 2 e 3 é 2,5, então dê a ambas as cinco a posição 2,5.

5. Na coluna `d`, calcule a diferença entre as duas posições em cada par de dados. Em outras palavras, se um tem a posição 1 e o outro tem a posição 3, a diferença é 2. (Positivo ou negativo não importa, já que vamos elevar ao quadrado essa diferença na próxima etapa.)

6. Eleve ao quadrado os valores na coluna d e escreva esses valores na coluna d.

7. Adicione todos os pontos de dados na coluna d. Este valor é Σd.

8. Escolha uma das fórmulas abaixo:

Se nenhum ponto de dados igual ocorreu nas etapas anteriores, insira Σd na fórmula simples para o coeficiente de correlação de classificação de Spearman

e digite o número de pares de dados para `n` para encontrar sua resposta.

Se pontos de dados semelhantes ocorreram nas etapas anteriores, use a fórmula padrão para o coeficiente de correlação de classificação de Spearman:

9. Interprete o resultado. Isso pode variar entre -1 e 1.

Perto de -1 - Correlação negativa.

Perto de 0 - Sem correlação linear.

Perto de 1 - Correlação Positiva.

Método 2 de 3: no Excel

1. Crie novas colunas com as posições das colunas existentes. Por exemplo, se você tiver seus dados na Coluna A2:A11, use a fórmula `=RANK(A2,A$2:A$11)` e estenda o intervalo em todas as suas linhas e colunas.

2. Trate pontos de dados iguais conforme descrito nas etapas 3 e 4 do método 1.

3. Em uma nova célula, faça um cálculo de correlação entre as duas colunas com uma fórmula como `=CORREL(C2:C11,D2:D11)`. Neste caso, C e D são as colunas de posição. O coeficiente de correlação de classificação de Spearman aparece na célula de correlação.

Método 3 de 3: Com R

1. Instale o R se você ainda não o tiver. (Ver https://www.r-projeto.org/.)

2. Salve seus dados como um arquivo CSV, com os dados que você deseja correlacionar nas duas primeiras colunas. Você pode fazer isso com o menu `Salvar como`.

3. Abra o editor R. Se você estiver trabalhando no terminal, basta executar R. Quando estiver na área de trabalho, clique no logotipo R.

4. Digite os seguintes comandos:

d <- ler.csv("NAME_OF_YOU_CSV.csv") e pressione enter

cor(rank(d[,1]),rank(d[,2]))

Pontas

Para a maioria dos conjuntos de dados, você precisa de pelo menos cinco pares de dados para estabelecer uma tendência (apenas três pares foram usados no exemplo para facilitar o exemplo).

Avisos

O coeficiente de correlação de classificação de Spearman só mostra a força da correlação se os pontos de dados estiverem aumentando ou diminuindo continuamente. Se o gráfico de dispersão dos pontos de dados mostrar uma tendência diferente, o coeficiente de correlação de classificação de Spearman aumentará a correlação não exibir corretamente.
Esta fórmula é baseada na suposição de que não há pontos de dados iguais. Se houver pontos de dados iguais, como no exemplo acima, use a seguinte definição: o coeficiente de correlação produto-momento para as classificações.