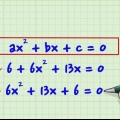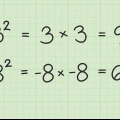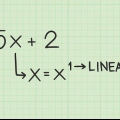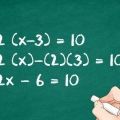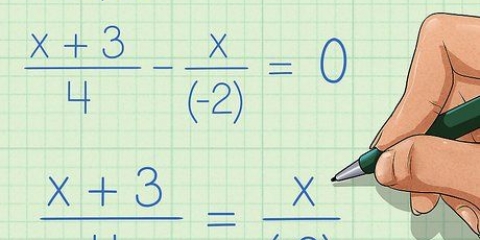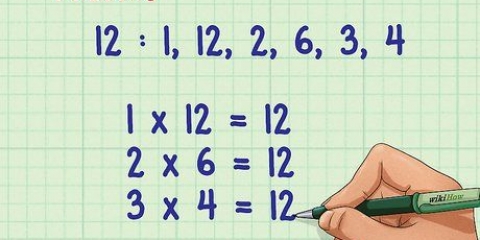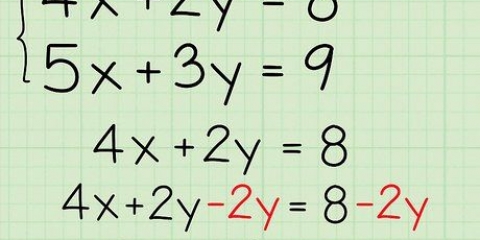Como 3x tem um número finito de fatores possíveis, 3x e x, você pode escrevê-los entre parênteses: (3x +/- ? )(x +/-- ?) = 0. Em seguida, use um método de eliminação onde você usa os fatores de 4 para encontrar uma combinação que dê -11x como resultado da multiplicação. Você pode usar uma combinação de 4 e 1, ou 2 e 2, porque a multiplicação de ambas as combinações de números produz 4. Tenha em mente que um dos termos deve ser negativo, porque o termo é -4. Tente (3x +1)(x -4). Quando você resolve isso, obtém - 3x -12x +x -4. Se você combinar os termos -12x e x, obterá -11x, que é o termo médio ao qual você queria chegar. Agora você fatorou esta equação quadrática. Outro exemplo; tentamos fatorar uma equação que não funciona: (3x-2)(x+2) = 3x +6x -2x -4. Se você combinar esses termos, obterá 3x -4x -4. Mesmo que o produto de -2 e 2 seja igual a -4, o termo médio não funciona porque você estava procurando -11x, não -4x. 

3x + 1 = 0 = 3x = -1 = 3x/3 = -1/3 x = -1/3 x - 4 = 0 x = 4 x = (-1/3, 4) 

Portanto, ambas as soluções funcionam separadamente e ambas são verificadas como funcionando e estão corretas em duas soluções diferentes. 



{-b +/-√ (b - 4ac)}/2 {-(-5) +/-√ ((-5) - 4(3)(-8))}/2(3) = {-(-5) +/-√ ((-5) - (-96))}/2(3) 
{-(-5) +/-√ ((-5) - (-96))}/2(3) = {5 +/-√(25 + 96)}/6 {5 +/-√(121)}/6 

(5 + 11)/6 (5 - 11)/6 
(5 + 11)/6 = 16/6 (5-11)/6 = -6/6 
16/6 = 8/3 -6/6 = -1 x = (-1, 8/3) 

2x - 12x - 9 = 0 2x - 12x = 9 
2x/2 - 12x/2 = 9/2 = x - 6x = 9/2 
-6/2 = -3 = (-3) = 9 = x - 6x + 9 = 9/2 + 9 


x = 3 +(√6)/2 x = 3 - (√6)/2)
Resolver equações quadráticas
Contente
Uma equação quadrática é uma equação onde o maior expoente de uma variável é dois. Três dos métodos mais usados para resolver essas equações são: fatoração, usando a fórmula abc ou dividindo o quadrado. Se você quiser saber como dominar esses métodos, basta seguir estes passos.
Degraus
Método 1 de 3: fatoração

1. Mover todos os termos para um lado da equação. O primeiro passo na fatoração é mover todos os termos para um lado da equação, deixando x positivo. Aplique a operação de adição ou subtração aos termos x, à variável x e às constantes, movendo-os para um lado da equação dessa maneira, não deixando nada do outro lado. Veja como isso funciona:
- 2x - 8x - 4 = 3x - x =
- 2x +x - 8x -3x - 4 = 0
- 3x - 11x = 0

2. Fatore a expressão. Para fatorar a expressão, você precisa fatorar os fatores de 3x e os fatores da constante -4 para multiplicá-los e depois somá-los para obter o valor do termo médio, -11. Veja como fazer isso:

3. Determine que cada par de parênteses é igual a zero e tratá-los como equações separadas. Isso faz com que você encontre dois valores para x que ambos tornam a equação inteira igual a zero. Agora que você fatorou a equação, tudo o que resta a fazer é tornar cada par de parênteses igual a zero. Então você pode escrever que: 3x +1 = 0 e x - 4 = 0.

4. Resolva cada equação. Em uma equação quadrática existem dois valores dados para x. Resolva cada equação separadamente isolando a variável e escreva os resultados de x. Aqui está como vai:

5. Verifique x = -1/3 pol (3x + 1)(x – 4) = 0:
Nós temos (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... substituindo:(-1 + 1)(-4 1/3) ?=? 0 ..... simplificando:(0)(-4 1/3) = 0 ..... multiplicando: então 0 = 0 ..... Sim, x = -1/3 funciona
Nós temos (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... substituindo:(-1 + 1)(-4 1/3) ?=? 0 ..... simplificando:(0)(-4 1/3) = 0 ..... multiplicando: então 0 = 0 ..... Sim, x = -1/3 funciona

6. Verifique x = 4 pol (3x + 1)(x - 4) = 0:
Obtemos (3[4] + 1)([4] – 4) ?=? 0..... substituindo:(13)(4 – 4) ?=? 0 ..... por escurecimento:(13)(0) = 0 ..... multiplicando: 0 = 0 ..... Sim, x = 4 funciona
Obtemos (3[4] + 1)([4] – 4) ?=? 0..... substituindo:(13)(4 – 4) ?=? 0 ..... por escurecimento:(13)(0) = 0 ..... multiplicando: 0 = 0 ..... Sim, x = 4 funciona
Método 2 de 3: Aplicando a fórmula Abc

1. Mova todos os termos para um lado da equação e mescle os termos semelhantes. Mova todos os termos para um lado do sinal de igual, mantendo o termo x positivo. Escreva os termos em ordem decrescente de magnitude, então x vem primeiro seguido por x, então a constante. Veja como fazer isso:
- 4x - 5x - 13 =x -5
- 4x - x - 5x - 13 +5 = 0
- 3x - 5x - 8 = 0

2. Escreva a fórmula abc. Isto é: {-b +/-√ (b - 4ac)}/2a

3. Determine os valores de a, b e c na equação quadrática. A variável uma é o coeficiente de x, b é o coeficiente de x e c é a constante. Para a equação 3x -5x - 8 = 0, a = 3, b = -5 ec = -8. Escreva isso.

4. Substitua os valores de a, b e c na equação. Agora que você já conhece os valores das três variáveis, basta colocá-las na equação como mostramos aqui:

5. Calcular. Depois de preencher os números, você resolve o problema ainda mais. Abaixo você pode ler como isso vai além:

6. Simplifique a raiz quadrada. Se o número sob o sinal de radical for um quadrado perfeito ou também um número quadrado, você obterá um número inteiro com a raiz quadrada. Em outros casos, simplifique a raiz quadrada o máximo possível. Se o número for negativo e você tiver certeza de que essa é a intenção, a raiz quadrada do número será menos simples. Neste exemplo, √(121) = 11. Você pode então escrever que x =(5 +/- 11)/6.

7. Resolva os números positivos e negativos. Depois de se livrar da raiz quadrada, você pode continuar até encontrar as respostas negativas e positivas para x. Agora que você tem (5 +/- 11)/6, você pode escrever as duas possibilidades:

8. Resolva as respostas positivas e negativas. Calcule mais:

9. Simplificar. Para simplificar, divida as respostas pelo maior número divisível pelo numerador e pelo denominador. Então divida a primeira fração por 2 e a segunda por 6 e você terá resolvido x.
Método 3 de 3: Dividindo o quadrado

1. Mova todos os termos para um lado da equação. Certifique-se de uma de x é positivo. Veja como fazer isso:
- 2x - 9 = 12x =
- 2x - 12x - 9 = 0
- Nesta equação, uma igual a 2, b é -12, e c é -9.

2. Mova a constante c para o outro lado. A constante é o valor numérico sem uma variável. Mova-o para o lado direito da equação:

3. Divida os dois lados pelo coeficiente da uma ou x termo. Se x não tiver nenhum termo na frente e tiver um coeficiente com o valor 1, você pode pular esta etapa. Nesse caso, você precisa dividir todos os termos por 2, assim:

4. Papel b por dois, eleve ao quadrado e some os resultados aos dois lados do sinal is.Ob neste exemplo é -6. Veja como fazer isso:

5. Simplifique os dois lados. Fatore os termos à esquerda para obter (x-3)(x-3), ou (x-3). Adicione os termos à direita para obter 9/2 + 9, ou 9/2 + 18/2, que soma 27/2.

6. Encontre a raiz quadrada de ambos os lados. A raiz quadrada de (x-3) é simplesmente (x-3). Você também pode escrever a raiz quadrada de 27/2 como ±√(27/2). Portanto, x - 3 = ±√(27/2).

7. Simplifique a raiz quadrada e resolva para x. Para simplificar ±√(27/2), procure um quadrado ou número quadrado perfeito com os números 27 ou 2 ou em seus fatores. O quadrado número 9 pode ser encontrado em 27, porque 9 x 3 = 27. Para eliminar 9 da raiz, escreva-o como uma raiz separada e simplifique para 3, a raiz quadrada de 9. Deixe √3 no numerador da fração porque ela não pode ser separada como um fator de 27, e faça de 2 o denominador. Em seguida, mova a constante 3 do lado esquerdo da equação para o lado direito e anote suas duas soluções para x:
Pontas
- Como você pode ver, o sinal radical não desapareceu completamente. Portanto, os termos no numerador não são mesclados (eles não são termos iguais). Então é inútil dividir os prós e contras. Em vez disso, dividindo, garantimos que todo fator comum desapareça – mas "SÓ" se o fator for igual para ambas as constantes, "E" o coeficiente da raiz quadrada.
Artigos sobre o tópico "Resolver equações quadráticas"
Оцените, пожалуйста статью
Popular